山东大学计算机图形学实验（Opengl实现）：Loop Subdivision算法对模型进行细分

最新推荐文章于 2025-02-14 03:24:02 发布

Tzankho

最新推荐文章于 2025-02-14 03:24:02 发布

阅读量2.1k

点赞数 2

分类专栏：计算机图形学文章标签：图形学 opengl 算法计算机视觉 c++

本文链接：https://blog.youkuaiyun.com/tzankho/article/details/111940563

版权

该博客介绍了如何使用Loop Subdivision算法对计算机图形学中的3D模型进行细分，以实现更平滑的表面效果。实验涉及了数据结构维护、效率考虑以及算法的具体实现步骤，包括新顶点的计算、旧顶点位置更新、三角形面片和边信息的重构，并强调了保持模型的拓扑正确性和效率。作者通过实验感受到了模型细分后的圆润感。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

一、实验目标/要求：
The goal of this assignment is to try your hand at various mesh processing tasks. A half-edge mesh adjacency data structure is provided, along with a very simple .obj mesh parser. As you modify the triangle mesh, it is critical that the manifold properties of the input surface are maintained, and that the adjacency data structure remains consistent. Throughout this assignment you are asked to consider the efficiency of various mesh operations: is it quadratic, linear, logarithmic, constant, etc? It’s ok if you don’t always implement the most efficient strategy (which may require additional data structures).
（上面的的意思大概就是利用Loop Subdivision算法对简单模型进行细分。）

二、实现效果：
第一组
请添加图片描述
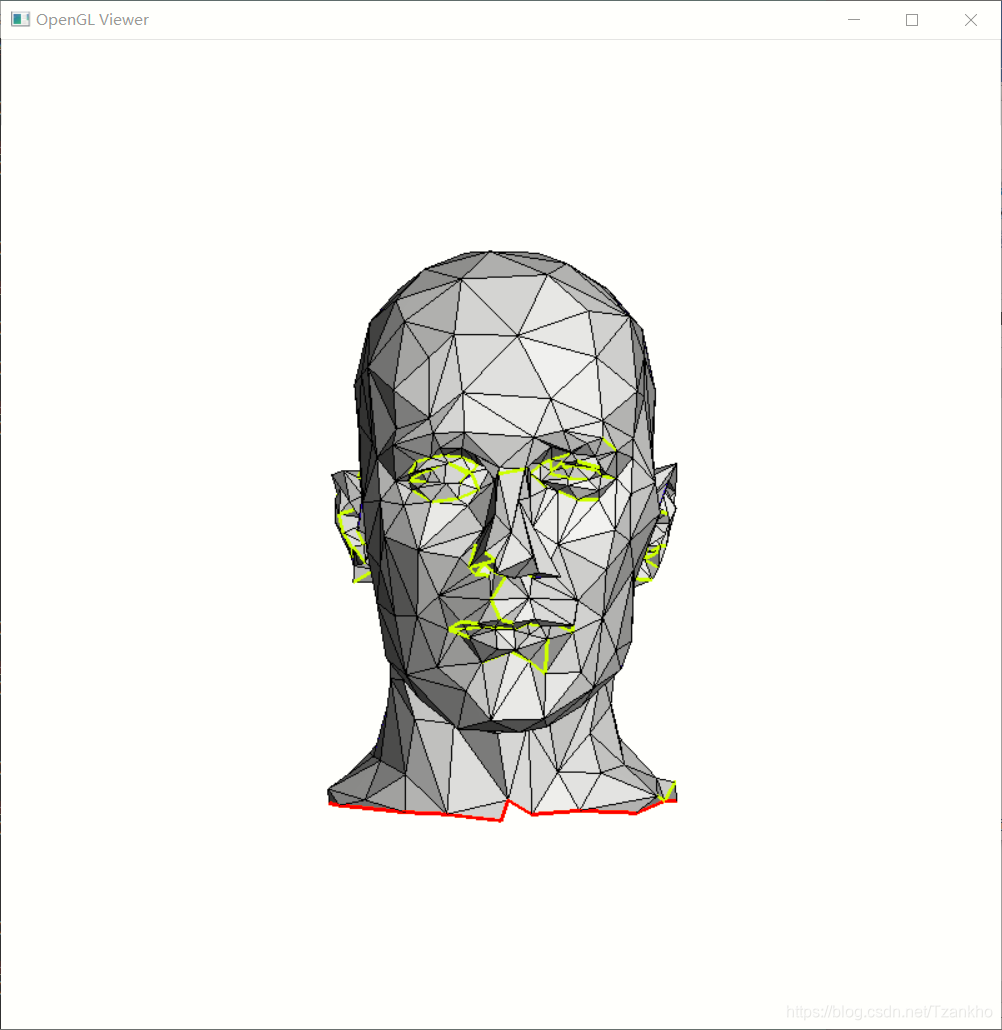
在这里插入图片描述

第二组
在这里插入图片描述

第三组
在这里插入图片描述

在这里插入图片描述

三、实现方法/思路：

先更新原来的旧顶点，根据旧顶点信息计算出新顶点位置信息并将计算的新位置信息和原来的点组成pair并储存在一个新的vector中（即下面算法中的update）。（另：此处要注意内部顶点和边界点的更新方式，公式不要出错）
分别根据内部边和和边界边不同的处理方式算出插入的新点的位置信息，然后直接向原来的点vector（即vertices）中插入（用addVertex函数）新顶点。
利用步骤1）中的vector（即update）来更新旧顶点的位置信息（用一个for循环和setPos函数即可）。
新建一个临时三角形面片的哈希表来存储旧三角形面片信息（即下面算法中的tempTriangles），然后清除旧三角形面片信息（triangles.clear()）和边信息(edges.clear())，然后再利用临时的三角形面片哈希表重构新的三角形面片信息和新的边信息（边信息是随着三角形面片信息的更新而更新的，不用管）。
修复一下这边信息，即为原来crease值不为零的边及其“衍生”的边重新附上crease值。
清空vertex_parents（这个玩意儿是通过一条边的两个端点去找边上所产生的新点的，在插入新店的步骤（即步骤2）中进行准备，用在重构三角形面片信息的步骤（即步骤4中），为下一次细分做准备。

算法代码如下：
（只包含算法部分的代码，不包含其余部分的代码，太多了，懒得整，嘿嘿）


void Mesh::LoopSubdivision()
{
   
    printf("Subdivide the mesh!\n");

    //store new position of old vertex in update.
    //(Traversal of all vertices)
    std::vector<std::pair<Vertex*, Vec3f>> update;
    for (edgeshashtype::iterator eIterator1 = edges.begin();
        eIterator1 != edges.end(); eIterator1++)
    {
   
        Edge* e = eIterator1->second;
        Edge* temp = e->getNext();
        Vec3f newPosition(0, 0, 0);
        std::vector<Vertex*> neighborVertices;

        while (temp->getOpposite() != NULL && temp->getOpposite() != e)
        {
   
            neighborVertices.push_back(temp->getEndVertex());
            temp = temp->getOpposite()->getNext();
        }

        if (temp->getOpposite() == NULL)
        {
   
            neighborVertices.clear();
            Vertex* v1

最低0.47元/天解锁文章