c++树的直径

一. 树的直径是什么？

给定一棵树，每条边上有边权，树上距离最远的两个点之间的距离叫树的直径。

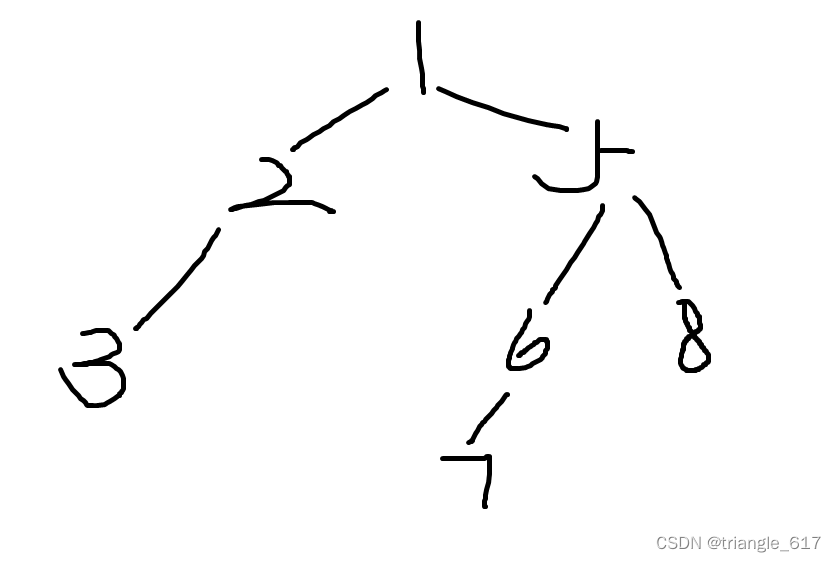
 如图，图中的直径为5。

二.树的直径的求法

我们可以先任意取一点进行一遍dfs求出离它最远的点a，再以求出的那个点再进行一次dfs求出离它最远的点b，此时a,b之间的距离就是树的直径。

三．代码实现

#include<bits/stdc++.h>

#define int long long

using namespace std;

struct node {

    int x, len;

};

vector<node> v[210000];//树

int dist[210000], s, t;//dist是点的距离，s、t是树的直径的两个端点

void dfs(int dep, int fa, int sum) {

    dist[dep] = sum;//求出距离

    for (int i = 0; i < v[dep].size(); i++) {

    if (v[dep][i] != fa)

    dfs(v[dep][i], dep, sum + 1);//遍历下去

}

}

signed main() {

    int n;

    scanf("%d", &n);

    for (int i = 1; i < n; i++) {

        int x, y, t;

        x = read();

        y = read();
        
        t = read();

        v[x].push_back({y, t});

        v[y].push_back({x, t});

    }//建树

    dfs(1, 0, 0);

    for (int i = 1; i < n; i++) if (dist[i] > dist[s]) s = i;

    //第一次遍历，求出树的直径的一个端点

    dfs(s, 0, 0);

    for (int i = 1; i < n; i++) if (dist[i] > dist[t]) t = i;

    //第二次遍历，求出树的直径的另一个端点

    cout << dist[t];

    return 0;

}