本文介绍VBRPCA
RPCA主要应用于矩阵恢复问题,一般形式为Y=L+S,其中Y是输入矩阵,L是低秩部分,S是稀疏部分。通过凸优化 ![]()
即可求解,一般可以采用ALM,IT,APG等方法。
在这一篇文章中,作者将输入矩阵视为Y=L+S+E,其中E是噪声项。![]()
将L和S分解,L=D(ZΔ)W,S=B·X,其中![]() ,Δ是对角矩阵,
,Δ是对角矩阵,![]() ,·运算为Hadamard product
,·运算为Hadamard product
也就是哈达玛积,定义为A·B=C,Cij=Aij*Bij。Z是二值对角矩阵,对角线上的元素只能为0或1,且Z是稀疏的。K表示L推断出最大可能的秩,通常情况下设置为一个很大的数。
低秩部分(L)
L=D(ZΔ)W,类似与SVD分解,但是引入了额外的Z矩阵,大小为K*K,引入的意义是为了解耦秩的学习和奇异值的学习。
Z被建模为![]() ,其中超参数α0,β0>0。
,其中超参数α0,β0>0。
又![]() ,为了加强Z的稀疏性,令α0/(α0+β0)<<1,这样pk就接近于0.
,为了加强Z的稀疏性,令α0/(α0+β0)<<1,这样pk就接近于0.
Δ中的元素表示为δkk,k=1,2,...,K 且![]() ,
,
同样的a0,b0>0
D和W的列D=[d1,d2,...,dK]和W[W1,W2,...,WM]被认为服从μ=0,Σ=1/N*IN的高斯分布,也即
其中I为N×N大小的单位矩阵,注意到当N和K很大时,D的列之间近似正交(W也是),这里,只强迫认为D的列跨越主向量空间(这里没明白),但是并不对正交性进行证明。
L的分解L=D(ZΔ)W同样可以从因子的角度来分析,L=[l1,...,lm]看作是
也就是说L的每一列可以看作是D中字典元素(每一列)的加权和,K为字典大小。
稀疏部分S:
稀疏部分分解为S=B·X,B是二值矩阵,B=[b1,...,bm]。B的每一列都可以被建模为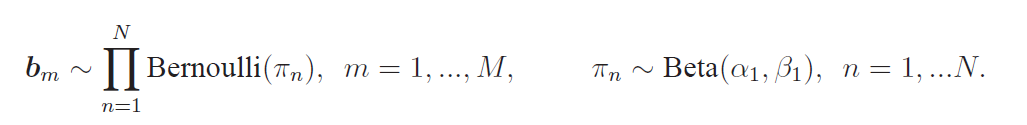
B中的每一列都共享一个系数πn,注意到这个模型对噪声具有鲁棒性,因为更新πn用的是B每一列的数据(后面会给到更新每个参数的公式)
X的每一列X=[x1,x2,...,xm]都认为是服从高斯分布![]()
并且令X的每一列都共享一个先验系数v,这样就可以降低算法复杂度。
噪声部分E:
E的模型为![]()
其中enm为E的第n行m列
文中提出,贝叶斯模型的全后验密度函数的负对数是 
Θ表示全部模型中的全部参数,H={α0,β0,α1,β1,a0,b0,c0,d0,e0,f0}是模型的超参数,
稀疏项在时间和空间上的马尔可夫性
作者在文中认为,如果是连续的视频帧,那么前后帧之间就会又一定的联系(事实也是这样),那么数据之间的独立同分布假设就是不恰当的。所以文中假设在稀疏部分在时间序列上满足马尔可夫性质。也就是说,在上一帧中如果有移动的物体存在,那么下一帧中同样有这个物体的可能性非常大。令Ft代表t时刻的稀疏分量,Ft(i,j)表示坐标位置。![]() 为Ft(i,j)的八邻域,
为Ft(i,j)的八邻域,
定义Ft(i,j)的状态为![]()

也就是说当这个点周围有大于ρ个点为激活状态时,它也是激活状态。这样t时刻这个点状态不仅与时间相关,同时也与空间相关。
通过上面的假设,可以将稀疏部分的公式重写为
对于t=1时刻,仍使用原来的公式。上式中H和L是马尔可夫树模型中用于压缩传感中小波系数的高和低状态
POSTERIOR INFERENCE
使用了MCMC和吉布斯采样以及变分贝叶斯推断。
参数更新:

MCMC的缺点是要经过大量的迭代,复杂度很高
变分贝叶斯推断通过一个q(Θ)去近似真正的参数p(Θ|Y),







 本文深入解析VBRPCA算法,一种结合变分贝叶斯推断的鲁棒主成分分析方法,用于矩阵恢复,将输入矩阵分解为低秩、稀疏及噪声三部分,通过引入额外矩阵增强解耦能力,实现更精准的矩阵分解。
本文深入解析VBRPCA算法,一种结合变分贝叶斯推断的鲁棒主成分分析方法,用于矩阵恢复,将输入矩阵分解为低秩、稀疏及噪声三部分,通过引入额外矩阵增强解耦能力,实现更精准的矩阵分解。
















 8
8

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








