不撞南墙不回头----深度优先搜索

前言：

       深度优先搜索属于图算法的一种，英文缩写为DFS即Depth First Search。其过程简要来说是对每一个可能的分支路径深入到不能再深入为止，而且每个节点只能访问一次。（即不撞南墙不回头）。

       举一个例子：

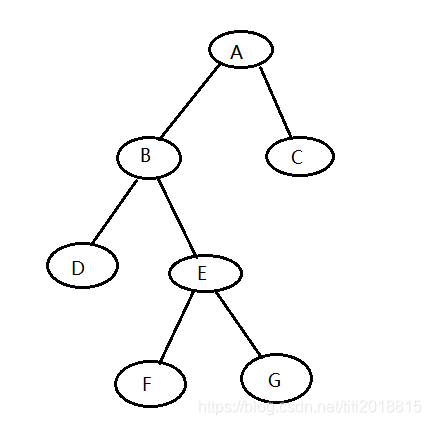
          对于这个图，从节点A进行深度优先搜索，（假设默认搜索都是先搜索左孩子，后搜索右孩子），那么搜索的顺序就是A-->B-->D-->E-->F-->G-->C;下面我来具体的模拟一下过程：第一个搜索的位置是A，A有两个孩子分别是B,C，但是我们默认搜索顺序是先左孩子后右孩子，所以下一个搜索的节点就是B，其中B也是有两个孩子，所以按照顺序我们要搜索左孩子D，对于D我们发现D没有孩子节点，这也就是我们说的撞到了南墙，那么接下来就要回头了，退回到节点B，节点B有两个孩子，但是节点D我们已经搜索过了，所以现在我们就要搜索节点E，到了节点E，我们发现节点E有两个子节点，我们下一步就要搜索节点F，F节点没有孩子节点（撞了南墙，所以现在要回头），退回到节点E，发现节点G没有走过，那么下一步就是走节点G，既然点G没有子节点，我们就要退回节点E，然后我们发现节点E的所有节点我们都走过，那么我们接着退回节点B，发现节点B的所有节点我们也是全部走过，那么我们接着退回节点A，发现节点C没有搜索过，那么我们就搜索节点C，节点C没有子节点，我们接着退，退回到节点A，我们发现节点A的所有节点我们都搜索过，那么这次以节点A开始的深度优先搜索就结束了。

        其实我们可以看出来，深度优先搜索算法就是在遍历整个图，把每一个节点都会走一遍，不停的尝试。其中在尝试的过程中有很多的退回，这个就是深度优先搜索中的回溯。看看上面我对于深度优先搜索过程的描述你就可以发现，整个算法在不停的搜索回溯，过程很麻烦，所以当你在比赛时就应该注意了，当地图的范围很大时就不能够使用深度优先算法，很容易超时。但是学好深度优先算法对于蓝桥杯还是很有优势的，填空题很多都要用到深搜。

       知道了深搜的方法，现在的问题就是如何用代码来实现。其实不难发现，深搜就是一个不停的递归，回溯的过程，我们只需要用一个数组来标记这个点是否被搜索过，然后不停的递归即可。深搜就是把所有的可能都走一遍，尝试所有的结果，这样可以帮助我们解决很多的问题。深搜我们大多数都是对于图的搜索，所以当我们碰到了问题，就是先要建图，然后再搜索。

       下面找一个关于深搜的简单的例子吧。

 

Lake Counting

POJ - 2386 就是一道简单的深搜问题（块连通问题）。

题目如下：

Due to recent rains, water has pooled in various places in Farmer John's field, which is represented by a rectangle of N x M (1 <= N <= 100; 1 <= M <= 100) squares. Each square contains either water ('W') or dry land ('.'). Farmer John would like to figure out how many ponds have formed in his field. A pond is a connected set of squares with water in them, where a square is considered adjacent to all eight of its neighbors.

Given a diagram of Farmer John's field, determine how many ponds he has.

Input

* Line 1: Two space-separated integers: N and M

* Lines 2..N+1: M characters per line representing one row of Farmer John's field. Each character is either 'W' or '.'. The characters do not have spaces between them.

Output

* Line 1: The number of ponds in Farmer John's field.

Sample Input

10 12
W........WW.
.WWW.....WWW
....WW...WW.
.........WW.
.........W..
..W......W..
.W.W.....WW.
W.W.W.....W.
.W.W......W.
..W.......W.

Sample Output

3

Hint

OUTPUT DETAILS:

There are three ponds: one in the upper left, one in the lower left,and one along the right side.

题意：

        有一个N*M的地图，其中“W”代表水，“.”代表干的地方，让你求出来整个地图中有多少的水坑。我们可以明显的看出来有三个水坑，接下来就是用代码来进行实现啦。这道题的连通性是指八个方位的连通。

思路：

       这道题我们就可以用刚刚学会的深度优先搜索算法啦，在开始的地图中，找到“W”就开始搜索，在搜索的过程中把“W”改成别的字符，代表着搜索过了，所有相连的都改变，那么我们可以发现，最后我们搜索的次数就是水坑的个数。最后输出结果就可以了。这个就是深搜的入门题，当然，我简化了过程，并没有用到数组的标记，但是把“W”改成别的字符也就代替了数组的标记，因为它也可以起到标记是否搜索过的作用。

代码如下：

#include<stdio.h>
#include<string.h>

int n,m,s;
char map[101][101];//存储地图；
int next[8][2]= {{1,0},{-1,0},{0,1},{0,-1},{-1,1},{-1,-1},{1,1},{1,-1}};//连通的八个方位；

void dfs(int x,int y)//搜索；
{
    map[x][y]='.';//把这一点的“W”改成“.”，代表搜索过；
    for(int i=0; i<8; i++)
    {
        int nx=x+next[i][0];//周围的坐标的位置；
        int ny=y+next[i][1];
        if(map[nx][ny]=='.')//这个点搜索过，或者这个点为干地，不能搜索，就结束；
            continue;
        if(nx<0||nx>=n||ny<0||ny>=m)//下一个坐标超出了地图的范围；
            continue;
        dfs(nx,ny);//这个点没有被搜索过，且这个点的范围没有超出地图的范围，所以就可以接着搜索下一步；
    }
    return ;
}


int main()
{
    while(~scanf("%d%d",&n,&m))
    {
        for(int i=0; i<n; i++)//输入地图；
            scanf("%s",map[i]);
        s=0;
        for(int i=0; i<n; i++)//开始搜索；
        {
            for(int j=0; j<m; j++)
            {
                if(map[i][j]=='W')//有水就开始搜索；
                {
                    s++;//水坑的数量增加；
                    dfs(i,j);//搜索；
                }
            }
        }
        printf("%d\n",s);
    }
    return 0;
}

上面的这道题，省略了数组标记的过程，那么就再来一道需要用数组标记的深搜来练练手吧。

马走日

OpenJ_Bailian - 4123

题目如下：

马在中国象棋以日字形规则移动。

请编写一段程序，给定n*m大小的棋盘，以及马的初始位置(x，y)，要求不能重复经过棋盘上的同一个点，计算马可以有多少途径遍历棋盘上的所有点。

Input

第一行为整数T(T < 10)，表示测试数据组数。
每一组测试数据包含一行，为四个整数，分别为棋盘的大小以及初始位置坐标n,m,x,y。(0<=x<=n-1,0<=y<=m-1, m < 10, n < 10)

Output

每组测试数据包含一行，为一个整数，表示马能遍历棋盘的途径总数，0为无法遍历一次。

Sample Input

1
5 4 0 0

Sample Output

32

思路：

        这道题就是明显的深度优先搜索的标准问题了（走完所有的点并且不重复，计算所有的方法），那么我们就可以用递归来不停的尝试，尝试所有的结果。

代码如下：

#include<stdio.h>
#include<string.h>

int map[10][10];//地图；
int t,n,m,x,y;
int sum=0;//结果；
int nextt[8][2]=
{
    {1,2},{1,-2},{-1,2},{-1,-2},{2,1},{2,-1},{-2,1},{-2,-1}
};//八个马能够走的位置，需要注意的是，中国象棋中的马是走“日”的；

void dfs(int a,int b,int s)//横坐标，纵坐标，已经搜索过的点的个数；
{
    if(s==n*m)//所有的点都被搜索过了；
        sum++;
    if(map[a][b]==0)//这个点为0，戴白哦这这个点没有被搜索过，即马没有走过；
    {
        map[a][b]=1;//现在把这个点标记为马走过了；
        for(int i=0; i<8; i++)//搜索从这个点出发，马可以走的其别的位置；
        {
            int nx=a+nextt[i][0];
            int ny=b+nextt[i][1];
            if(nx<0||nx>=n||ny<0||ny>=m)//超出地图的范围了，不可以；
                continue;
            if(map[nx][ny]==1)//这个点走过了，不可以；
                continue;
            dfs(nx,ny,s+1);//符合条件的就搜索，记得搜过的点的个数要加一；
        }
        map[a][b]=0;//超级重要，记得把刚刚改的标记再改回来，
        //因为要尝试所有的结果，这个点不改回来会对下一次的尝试有影响；
    }
    return ;
}

int main()
{
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d%d%d",&n,&m,&x,&y);
        memset(map,0,sizeof map);//清0，代表这个点没有走过；
        sum=0;
        dfs(x,y,1);
        printf("%d\n",sum);
    }
    return 0;
}