机器学习详解(22):Focal Loss损失函数(解决类别不平衡)

在目标检测、分类等任务中，类别不平衡是常见难题，传统交叉熵损失在这种情况下容易导致模型偏向多数类。为了解决这个问题，Focal Loss被提出，它通过调制因子 $\gamma$和类别权重 $\alpha$，压低容易样本的损失，同时增强少数类的重要性，从而改善模型训练效果。

1 交叉熵损失函数

1.1 介绍

在很多任务中，比如目标检测、文本分类等，模型训练时的损失函数常用Cross Entropy。这个损失函数的核心思想是：对正样本要预测出高概率，对负样本要预测出低概率。这样我们可以通过一个阈值(比如0.5)来简单地区分正负类。

下图展示了二分类交叉熵的损失函数：

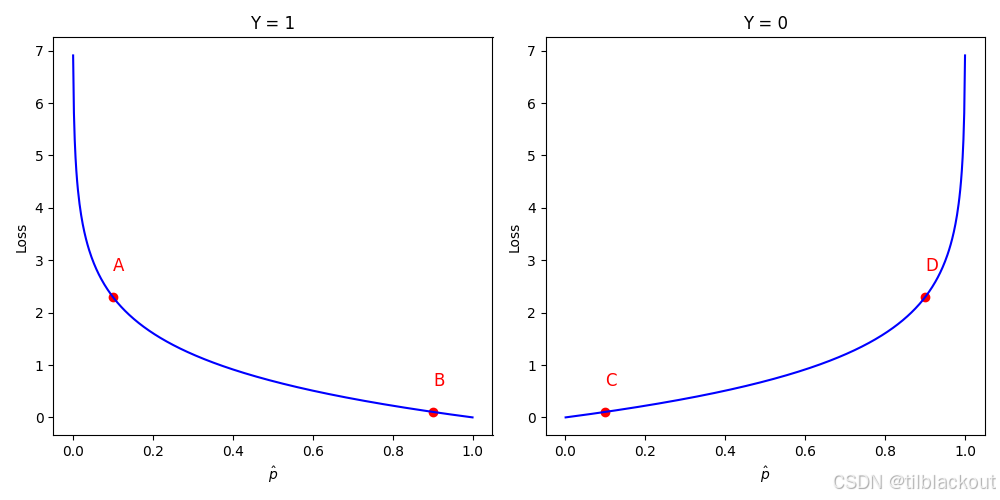
图中横轴表示模型对正类的预测概率 $\hat{p}$，纵轴表示损失值。我们把它拆成两种情况来看：

1. 当真实标签 $Y=1$ 时，损失是 $-\log (p)$：

   • 如果模型预测 $\hat{p}$ 很小(靠近0)，就会被严重惩罚(图中A点)。
   • 如果预测 $\hat{p}$ 很大(靠近1)，说明预测得不错，损失也很小(图中B点)。

2. 当真实标签 $Y=0$ 时，损失是 $-\log (1-p)$：

   • 如果预测 $\hat{p}$ 很小，表示模型认得出负样本，损失小(图中C点)。
   • 如果预测 $\hat{p}$ 靠近 1，那就是错误预测，损失就很大(图中D点)。

综合两个公式，我们写成：

$$CE(p,y)=\{\begin{array}{ll}-\log (p),& \text{if }y=1\\ & \\ -\log (1-p),& \text{if }y=0\end{array}$$

推广到多分类情况($N$类)，Cross Entropy Loss写为：

$$CE=-\sum y_i\log (p_t)$$

这个损失函数的本质在于：根据预测结果与真实标签之间的差距进行惩罚，差距越大，惩罚越重。它并不会考虑类别是否均衡，而是对所有样本都一视同仁(class-agnostic)，也就是不会因为你是正类还是负类、主类还是少数类而改变它的惩罚力度。

1.2 问题

Cross Entropy 最大的问题在于：当类别极度不均衡时，假设负类远多于正类，模型会被简单的负例牵着走，而不是去学那些真正困难的正例。因为只要把负例分对了，大多数损失就能减小

以目标检测为例：

大多数图像中都是背景($Y=0$)，只有极少数像素/区域是目标($Y=1$)。这个情况我们称为类不平衡(class-imbalance)。这个问题带来了两个具体影响：

a)负例太简单，模型学不到东西

模型一开始就很容易学会分辨负类。训练后期，绝大部分负例都变成easy negative，它们对模型的训练几乎没有帮助。训练效率低下。

b)大量简单负例主导了损失

负例数量太多了，即使每个负例损失很小，加起来也能占据损失函数的大头，导致模型的优化方向偏了。比如：

• 一个高置信度的负类预测贡献损失： $-\log (1-p)=-\log (0.95)=0.05$
• 一个高置信度的正类预测也贡献： $-\log (p)=-\log (0.95)=0.05$

这两个损失一样大，但因为负例数量远多于正例，最终梯度大多来自负例，导致模型越来越会判断背景，却无法判断目标。

2 Focal Loss

常见的解决方法包括只训练困难样本(hard negative mining)、欠采样或过采样等数据增强方法。

但有没有可能在不动数据集的前提下，直接修改损失函数来解决这个问题？

这就是 Focal Loss 的动机。Facebook AI(FAIR)团队在 2018 年 RetinaNet 中首次提出了这个损失函数。

Focal Loss 解决了什么问题？

1. 让模型关注困难的样本而不是轻松分类的容易样本
2. 在正负类之间找到一个更合理的平衡方式

总结一句话： 损失函数要能够压低容易样本的权重，集中精力在那些真正难学的样本上。

2.1 易样本 vs 难样本

首先我们需要让模型少关注容易的样本，多关注难的样本。

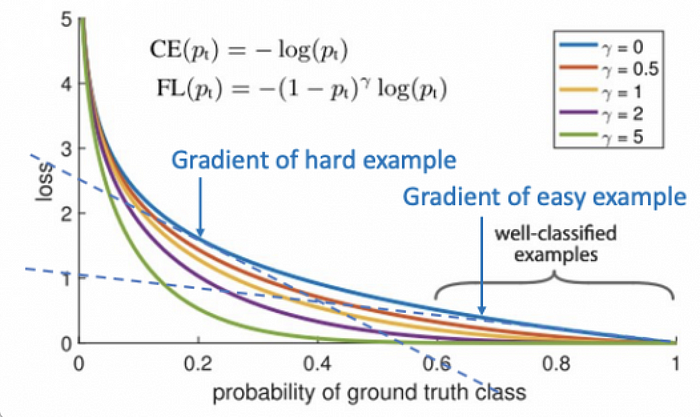
为此我们引入一个新的参数：调制因子 $\gamma$。当 $\gamma =0$ 时，Focal Loss 等价于普通的交叉熵(CE)，即图中蓝色曲线；此时的损失对高置信度的预测仍然不小。

我们希望的是：对于容易被模型正确预测的样本(即 $\hat{p}$ 很大)，它的损失应该更小。比如 $\hat{p}>0.5$ 的情况下，不应该还有太大的损失值。

因此，我们通过调高 $\gamma$ 值(如 $\gamma =5$)，来让更多置信度较高的预测(哪怕不完美)也获得极小的损失值。如下公式引入调制因子 $\gamma$：

$$FL(p_t)=-(1-p_t{)}^{\gamma }\log (p_t)$$

• $\gamma$ 越大，表示放过越多预测得还算不错的样本
• 换句话说，这让模型把更多注意力集中在那些置信度很低的样本(难样本)上

这种设计的核心在于：如果样本已经被很好地分类($p_t$ 接近 1)，那就不用再为它分配太多的损失值，也不值得模型再努力优化它。

当 $\gamma =0$ 时，Focal Loss 退化成普通的交叉熵；我们可以通过交叉验证去调节 $\gamma$ 的值，推荐范围一般是 1 到 5。

总结：调制因子 $\gamma$ 让损失对容易分类的样本迅速衰减，扩大了什么样的预测可以被视作正确的，让模型更关注错误严重的预测。

2.2 正负类不平衡

虽然 $\gamma$ 解决了难 vs 易的样本聚焦问题，但没有处理类别不均衡的问题。

因此我们引入另一个参数 $\alpha$，它通常取决于类别频率的倒数，用于加权不同类别的样本。形式如下：

$$FL(p_t)=-{\alpha }_t\log (p_t)$$

其中：

• ${\alpha }_t=\alpha$ 用于正类
• ${\alpha }_t=1-\alpha$ 用于负类

最终，我们将两种调整合并，得到Focal Loss完整版本：

$$FL(p_t)=-{\alpha }_t(1-p_t{)}^{\gamma }\log (p_t)$$

二分类情况下($y=1$和$y=0$)，写成完整条件表达式为：

$$FL(p)=\{\begin{array}{ll}& \\ -\alpha (1-p{)}^{\gamma }\log (p),& y=1\\ & \\ & \\ -(1-\alpha )p^{\gamma }\log (1-p),& y=0\end{array}$$

实际上， $\alpha$就是人为给不同类别加权，假设负类更多，那么正类样本的loss被放大，负类样本的loss被缩小。

2.3 二分类例子

我们用一个表格来对比普通交叉熵(简写为CE)与 Focal Loss(简写为FL)在不同样本情况(容易 vs 困难、正类 vs 负类)下的损失表现，进一步说明 Focal Loss 的聚焦能力。

假设参数为：$\gamma =2$, $\alpha =0.25$

• 在实际中更常用的是 $\alpha =0.75$，因为正类往往是少数类，需要提高其权重。

难度类别	正类 ($Y=1$)	负类 ($Y=0$)
容易样本	预测概率 $p=0.9$ CE = 0.105 FL = 0.00026 CE/FL ≈ 400	预测概率 $p=0.1$ CE = 0.105 FL = 0.0007 CE/FL ≈ 150
困难样本	预测概率 $p=0.1$ CE = 2.302 FL = 0.466 CE/FL ≈ 5	预测概率 $p=0.9$ CE = 2.302 FL = 1.399 CE/FL ≈ 2

从表中可以看出Focal Loss能够聚焦在难分的样本上：

• 对于容易分类的样本，Focal Loss会将它们的损失显著压缩(减少100倍以上)，从而减少模型在这些样本上浪费精力
• 对于困难样本，损失几乎没有被削弱，模型依然会重点优化这些样本

极端案例

假设：有1000000个负类样本，预测概率 $p=0.99$(非常自信地预测成负类)；有10个正类样本，预测概率 $p=0.01$(非常不自信)

使用普通交叉熵(CE)时：

• 每个负类样本的损失约为 $0.00436$，总负类损失：$1,000,000\times 0.00436=4364$
• 每个正类样本的损失约为 $2$，总正类损失：$10\times 2=20$
• 正类损失占比仅为：$20/(4364+20)\approx 0.0046$，几乎可以忽略

使用Focal Loss($\gamma =2$, $\alpha =0.25$) 时：

• 每个负类损失被缩小为约$0.0000003274$，总负类损失仅为：$0.3274$
• 每个正类样本损失调整为约 $0.49$，总正类损失为：$4.901$
• 正类损失占比升高至：$4.901/(4.901+0.3274)\approx 0.9374$

结论：

Focal Loss 有效地压制了大量容易负类的影响力，使得模型无法忽视少数正类的错误，从而增强了对困难和少数类的学习能力。

3 总结

Focal Loss通过两项机制缓解类别不平衡：$\gamma$ 让模型聚焦困难样本，$\alpha$ 提升少数类的权重。相比普通交叉熵，它能更有效引导模型学习关键样本，在许多实际场景中表现更优。