CodeForces 1084D The Fair Nut and the Best Path —— 找一条获得-花费最大的路径

The Fair Nut is going to travel to the Tree Country, in which there are n cities. Most of the land of this country is covered by forest. Furthermore, the local road system forms a tree (connected graph without cycles). Nut wants to rent a car in the city u and go by a simple path to city v. He hasn’t determined the path, so it’s time to do it. Note that chosen path can consist of only one vertex.

A filling station is located in every city. Because of strange law, Nut can buy only wi liters of gasoline in the i-th city. We can assume, that he has infinite money. Each road has a length, and as soon as Nut drives through this road, the amount of gasoline decreases by length. Of course, Nut can’t choose a path, which consists of roads, where he runs out of gasoline. He can buy gasoline in every visited city, even in the first and the last.

He also wants to find the maximum amount of gasoline that he can have at the end of the path. Help him: count it.

Input
The first line contains a single integer n (1≤n≤3⋅105) — the number of cities.

The second line contains n integers w1,w2,…,wn (0≤wi≤109) — the maximum amounts of liters of gasoline that Nut can buy in cities.

Each of the next n−1 lines describes road and contains three integers u, v, c (1≤u,v≤n, 1≤c≤109, u≠v), where u and v — cities that are connected by this road and c — its length.

It is guaranteed that graph of road connectivity is a tree.

Output
Print one number — the maximum amount of gasoline that he can have at the end of the path.

Examples
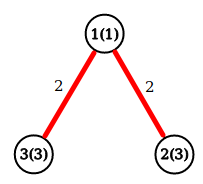
Input
3
1 3 3
1 2 2
1 3 2
Output
3
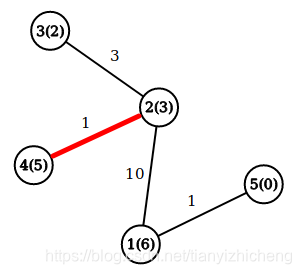
Input
5
6 3 2 5 0
1 2 10
2 3 3
2 4 1
1 5 1
Output
7
Note
The optimal way in the first example is 2→1→3.

The optimal way in the second example is 2→4.

题意：

给你n个点，n-1条边，你可以从任一点出发，任一点结束，但是要构成简单路径！！！就是没有环，没有重边的路径，每一个点都有一个值，走过一条边要消耗边上的值，问你最多能有多少值

题解：

刚开始没有看到简单路径，想不出来怎么处理来回的情况，最后别人告诉我原来是这么回事= =
那么这道题就是dfs一遍，找到剩余最多的值就好了

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const int N=3e5+5;
ll w[N];
struct node
{
    int to,next;
    ll wei;
}e[N*2];
int cnt,head[N];
void add(int x,int y,ll w)
{
    e[cnt].to=y;
    e[cnt].wei=w;
    e[cnt].next=head[x];
    head[x]=cnt++;
}
ll maxn,dp[N];
int vis[N];
void dfs(int x,int fa)
{
    maxn=max(maxn,dp[x]);
    vis[x]=1;
    for(int i=head[x];~i;i=e[i].next)
    {
        int ne=e[i].to;
        if(ne==fa||vis[ne])
            continue;
        dfs(ne,x);
        maxn=max(maxn,dp[x]+dp[ne]-e[i].wei);
        dp[x]=max(dp[x],w[x]+dp[ne]-e[i].wei);
    }
}
int main()
{
    memset(head,-1,sizeof(head));
    int n;
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%lld",&w[i]),dp[i]=w[i];
    int x,y;
    ll w;
    for(int i=1;i<n;i++)
    {
        scanf("%d%d%lld",&x,&y,&w);
        add(x,y,w),add(y,x,w);
    }
    dfs(1,0);
    printf("%lld\n",maxn);
}