| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 2917 | Accepted: 1450 |
Description
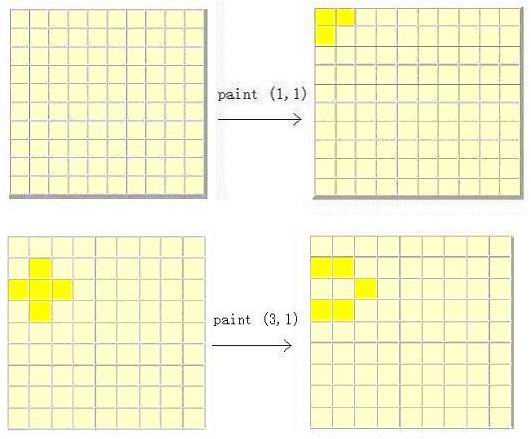
Input
Output
Sample Input
2 3 yyy yyy yyy 5 wwwww wwwww wwwww wwwww wwwww
Sample Output
0 15
题意:
刷墙每次刷一格会将上下左右中五个格子变色,求最少的刷方法使得所有的格子都变成yellow。
分析:
与POJ1185 炮兵阵地 有相似之处,状态枚举和位运算。同样从第一行开始枚举所有粉刷状态,然后后面每行每格paint[k][p]的粉刷情况要根据wall[k-1][p]经过paint[k-1][p]、paint[k-1][p-1]、paint[k-1][p+1]、paint[k-2][p]后的情况而定。若为1(即白色)则paint[k][p]=1。所有行处理完后,判断墙壁是否已经全为黄色,并记录下paint[i][j]为1的个数。循环至第一行枚举了0000 - 1111所有状态。
程序源代码如下:
#include <iostream>
using namespace std;
bool wall[18][18];
bool paint[18][18];
int count=0;
int mmin=300;
bool allYellow(int n)
{
int i,j;
count=0;
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
{
if(wall[i][j]^paint[i][j]^paint[i][j-1]^paint[i][j+1]^paint[i-1][j]^paint[i+1][j])return false;
if(paint[i][j])count++;
}
}
return true;
}
int main()
{
freopen("in.txt","r",stdin);
int t,n;
cin>>t;
int i,j,k,p;
char wy[16];
int mmax,tmp;
bool possible=false;
for(i=0;i<t;i++)
{
cin>>n;
memset(wall,0,sizeof(wall));
for(j=1;j<=n;j++)
{
cin>>wy;
for(k=0;k<n;k++)
{
if(wy[k]=='w')wall[j][k+1]=true;
}
}
mmax=1<<n;
mmin=300;
possible=false;
for(j=0;j<mmax;j++) //第一行的状态 0000 - 1111 枚举
{
memset(paint,0,sizeof(paint));
tmp=j;
for(k=1;k<=n;k++) //第一行的状态
{
paint[1][k]=tmp&1;
tmp=tmp>>1; //右移一位
}
for(k=2;k<=n;k++)
{
for(p=1;p<=n;p++) //根据wall[k-1][p]的paint后状态 决定paint[k][p]值
{
if(wall[k-1][p]^paint[k-1][p]^paint[k-1][p-1]^paint[k-1][p+1]^paint[k-2][p])paint[k][p]=true;
}
}
if(allYellow(n))
{
possible=true;
if(mmin>count)mmin=count;
}
}
if(possible)cout<<mmin<<endl;
else cout<<"inf"<<endl;
}
return 0;
}







 本文探讨了一种解决在给定约束条件下最小化刷墙次数的问题,通过位运算和状态枚举的方法来优化算法效率,确保所有墙面最终变为黄色。
本文探讨了一种解决在给定约束条件下最小化刷墙次数的问题,通过位运算和状态枚举的方法来优化算法效率,确保所有墙面最终变为黄色。
















 5626
5626

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








