矩阵乘法求斐波那契数列（快速幂）

首先介绍矩阵乘法：

定义：设A=(

   

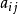)为

   

的矩阵，B=（

   

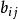)为

   

的矩阵，那么称

   

的矩阵C=（

   

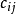)为矩阵A与B的乘积，记作

   

，其中矩阵C中的第

   

第

   

列元素为

由定义可知，

1：当矩阵A的列数等于矩阵B的行数时，A与B可以相乘。

2：矩阵C的行数等于矩阵A的行数，C的列数等于B的列数。

3：乘积C的第

   

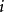行第

   

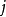列的元素

   

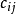等于矩阵A的第

   

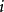行的元素与矩阵B的第

   

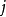列对应元素乘积之和。

c[i][j]=Σa[i][k]*b[k][j]。

例如：

 

，

 

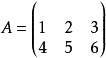
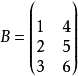
定义矩阵

 

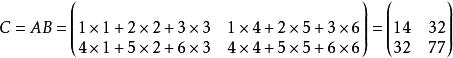
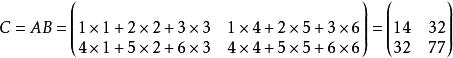
注意 矩阵乘法一般不满足交换律。即:

 

然后由该数列定义可知，

所以目的就是求出前面的系数，需要用到快速幂（当然，如果比较小的话就不需要了，其实如果比较小也不需要用矩阵。。。）

至于快速幂就是和普通的是一样的，只是相乘就需要用到矩阵相乘啦。

</pre><pre name="code" class="cpp">#include <cstdio>
#include <iostream>
using namespace std;
int T,n;
long long q;
struct aaaa{
   long long a[2][2];
}base,ans;
void get_f(void);
aaaa cheng(aaaa a,aaaa b);
int main()
{
    cin>>T;
	while(T--){
	   cin>>n>>q;
	   get_f();
	   cout<<(ans.a[1][0]+ans.a[1][1])%q<<endl;
	}
return 0;
}
void get_f(void)
{
    ans.a[0][0]=ans.a[1][1]=1;
	ans.a[0][1]=ans.a[1][0]=0;
	base.a[0][0]=base.a[0][1]=base.a[1][0]=1;
	base.a[1][1]=0;
	while(n>0){//特别说明，之前说是n-1次，那么我使用下面的f[(n+1)-1]就是f[n]了
	    if(n&1){
		    ans=cheng(ans,base);
		}
		base=cheng(base,base);
		n=n>>1;
	}
}
aaaa cheng(aaaa a,aaaa b)
{
    aaaa x;
	x.a[0][0]=a.a[0][0]*b.a[0][0]+a.a[0][1]*b.a[1][0];
	x.a[0][0]%=q;
	x.a[0][1]=a.a[0][0]*b.a[0][1]+a.a[0][1]*b.a[1][1];
	x.a[0][1]%=q;
	x.a[1][0]=a.a[1][0]*b.a[0][0]+a.a[1][1]*b.a[1][0];
	x.a[1][0]%=q;
	x.a[1][1]=a.a[1][0]*b.a[0][1]+a.a[1][1]*b.a[1][1];
	x.a[1][1]%=q;
	return x;
}