Homework1 of information basis II

The question1: what the normed linear space(赋范线性空间) is?

For sloving the question, I will divide it into two parts, which are norm and linear space!

what the distance is?There are three kinds of distance. 

condition 1:  Euclidean distance and that is 

condition 2 :

condition 3:   which is called manhattan distance

And no matter which kind distance, they all satisfy the three rules above.

We can add another rule so that we can get a more concrete idea that we call norm.

There are also three cases of norm corresponding to distance:

what is linear space?

The vector spaces which satisfiy the eight rules are linear space!

 A linear space that has a norm is called an normed linear space.

 

Question 2:The definition of a graph in computer science.

In the processing of finishing, I found a very good blog, which speaks very comprenhensive and I share it here:

https://blog.youkuaiyun.com/qq_35644234/article/details/57083107

 

Question 3:someting about activation functions

https://www.jiqizhixin.com/articles/2017-11-02-26

I can always find good articles which can solve my questions!

 

Question 4:compact supset of 

https://blog.youkuaiyun.com/foolely/article/details/1350785    LOL

 

Question5：Why can neural networks approach arbitrary continuous functions infinitely?

https://zhuanlan.zhihu.com/p/25590725

This is a article on www.zhihu.com and I think neural networks can solve nonlinear functions by increasing the numbers of neural cells and adjusting parameters.

 

Question6:Calculate the relationship between output y and input x in the condition of only one hidden layers

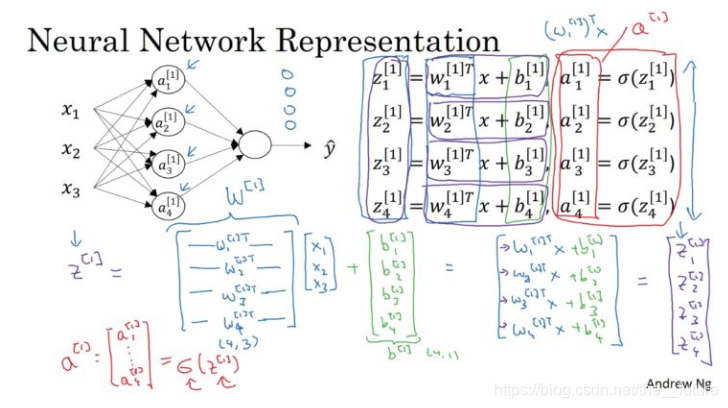
This slide is from Andrew Ng's courese called deep learing on coursehero. And it clearly shows the process of calculating.