1、Fibonacci Sequence - 斐波那契数列，第n项的值？

斐波那契数列（Fibonacci sequence），又称黄金分割数列、因数学家列昂纳多·斐波那契（Leonardoda Fibonacci）以兔子繁殖为例子而引入，故又称为“兔子数列”

问题如下：

有一对兔子，从出生后第3个月起每个月都生一对兔子，小兔子长到第三个月后每个月又生一对兔子，假如兔子都不死，问每个月的兔子对数为多少？

有如下序列 ：

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233，377，610，987，1597，2584，4181，6765，10946，17711，28657，46368…

可以发现这个数列从第3项开始，每一项都等于前两项之和；

有两种解决思路：

1、自底向上的分析，是从具体到抽象；依赖于“子问题”的求解；

2、自顶向下的分析，是从抽象到具体；

思路一：

从第三项起，将前面两项之和赋值给下一项，循环赋值迭代直到要求的第n项；

 static long fibonacciNum(int n){
        if(n <= 0) return 0;
        if(n == 1) return 1;
        long prev1=1,prev2=1;
        long current = 0;
        for(int i = 2; i < n; i++){
            current = prev1 + prev2;
            prev1 = prev2;
            prev2 = current;
        }
        return current;
    }

一个for循环，时间复杂度O(n);

思路二：

以递推的方法定义：F(1)=1，F(2)=1, F(n)=F(n-1)+F(n-2)（n>=3，n∈N*）；

根据递推公式，编写出求斐波那契数列的递归法：

  static long fibonacciNum(int n){
        if(n <= 0) return 0;
        if(n == 1) return 1;
        return fibonacciNum(n-2) + fibonacciNum(n-1);
  }

新的问题：递归法在求前面数值较小项时速度没有明显差别，但是随着n值的增大，递归的弊端也显现了出来，n为50时已经要30s计算出来，再往后难以想象。

虽然递归算法简洁，但是在这个问题中，它的时间复杂度却是难以接受的。除此之外，递归函数调用的越来越深，它们在不断入栈却迟迟不出栈，空间需求越来越大，虽然访问速度高，但大小是有限的，最终可能导致栈溢出。

借用一张图，地址：

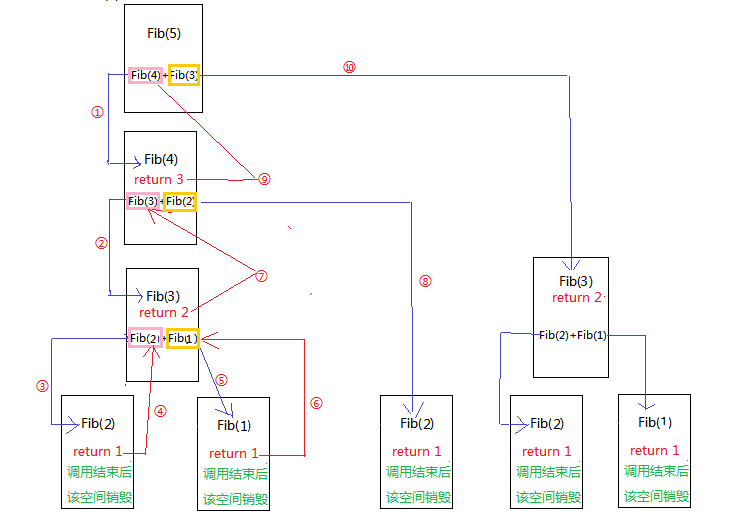
展示了递归调用的过程，可以看出来重复计算了很多相同的值，在时间上造成了很大的浪费，算法的时间复杂度随着n的增大呈现指数增长，时间的复杂度为O(2^n)，即2的n次方；

优化的方法是把计算过的结果存放起来，每次计算前查看是否已经存在相同的节点，如果有则直接返回，否则将此新节点添加至数组中；优化后代码：

 private static HashMap<Integer,Long> map = new HashMap<>();
    static long fibonacciNum3(int n){
        if(n <= 0) return 0;
        if(n == 1) return 1;
        if(map.containsKey(n)){
            return map.get(n);
        }else{
            long current = fibonacciNum3(n-2) + fibonacciNum3(n-1);
            map.put(n,current);
            return current;
        }
    }

优化后的程序相当于给之前的递归树做了剪枝操作，相同的节点仅执行一次，因此时间复杂度降为 O(n) 。