基于自然驾驶数据的RSS模型校准

使用自然驾驶研究数据对自动驾驶跟车操作的责任敏感安全模型进行校准与评估

摘要

安全性保障对于自动化车辆（AV）的可靠性至关重要，因此也是自动驾驶汽车工业和监管机构关注的重点。由Mobileye提出的责任敏感安全（RSS）是一种严格的数学模型，用于定义自动驾驶车辆相对于周围车辆需要保持的实时安全距离，并帮助自动驾驶车辆应对危险情况。然而，RSS的性能尚未通过真实驾驶数据进行测试。因此，本研究基于从上海自然驾驶研究中检测到的安全关键事件（SCEs）所构建的跟车场景，对RSS模型进行了标定和评估。SCEs通过触发方法从原始数据中识别出来，经过人工验证后，被转换为虚拟场景，在这些场景中，人工驾驶的试验车辆被替换为由嵌入RSS的基于模型预测控制的自适应巡航控制（ACC）系统控制的自动驾驶车辆。RSS模型的标定目标是实现最佳安全性表现，即在将自动驾驶汽车算法应用于安全关键场景后，使时间积分碰撞时间（TIT）最低。通过比较嵌入RSS的ACC、仅ACC以及无辅助的人类驾驶员的表现，本研究发现：1）在控制每个15秒事件的平均TIT为2.65秒²的情况下，嵌入RSS的ACC在消除潜在安全关键情况方面表现最优；2）嵌入RSS的ACC产生了最高的平均相对速度和相对距离，以及最低的速度标准差；3）平均而言，嵌入RSS的ACC能够比人类驾驶员提前2.31秒感知安全关键事件。

引言

自动驾驶车辆（AV）技术一直是交通工程领域的热门话题，因其有望成为解决当前交通问题的最佳方案，例如提升交通安全性和最大限度利用道路资源。然而，根据加州机动车管理局发布的最新自动驾驶汽车脱离报告，2018年在加州进行自动驾驶汽车试驾的28家公司平均脱离率为每1000英里163.79次脱离，即自动驾驶车辆需要手动恢复车辆控制的频率为每1000英里163.79次（自动驾驶汽车脱离报告，2018）。持续较高的脱离率引发了公众对自动驾驶车辆可靠性的质疑。近年来涉及自动驾驶汽车的碰撞事故，例如优步2018年在亚利桑那州发生的自动驾驶致命碰撞事故，加深了人们对于提升自动驾驶车辆安全性表现的紧迫感和必要性。另一个与自动驾驶车辆安全性相关的担忧是，当自动驾驶车辆卷入碰撞事故时，如何分配责任。由于保密性以及深度学习黑箱特性导致自动驾驶汽车算法缺乏透明度和可解释性，使得难以确定导致碰撞的真实因素，从而难以判定责任归属。

确保自动驾驶车辆’安全性和可靠性的一个重要手段是建立一个能够被行业和监管机构采纳的规范化安全模型。该模型应能够以广泛接受的方式定义在发生碰撞时的责任。2017年，Mobileye的研究人员提出了责任敏感安全（RSS）模型，旨在确保自动驾驶车辆足够谨慎，不会引发碰撞，并能够合理应对其他驾驶员的错误（Shalev‐Shwartz 等人，2017）。该模型用于计算自动驾驶车辆在纵向和横向必须保持的实时安全距离，并帮助自动驾驶车辆妥善应对危险情况。安全距离的定义基于最坏情况假设。也就是说，只要遵守RSS安全距离，即使周围车辆出现极端动作时自动驾驶车辆未施加全力制动，仍可保证安全。形象地说，RSS模型将自动驾驶车辆包裹在一个“安全包络”中。“安全包络”一旦该包络被其他交通参与者侵入，自动驾驶车辆应以预设的减速度减速。

RSS模型的优势可以总结如下：1) RSS是一个严谨的数学模型，涵盖了自动驾驶车辆的三个主要任务：感知、规划和执行；2) “最坏情况假设”消除了对其他交通参与者意图进行预测的需求；3) 当车辆之间的相对距离不再满足最小安全距离时，RSS模型能够根据各主体是否正确遵守RSS响应约束来确定碰撞责任方；4) 如先前研究所示，RSS模型能够覆盖美国国家公路交通安全管理局（NHTSA）研究中提出的全部多主体碰撞前场景，包括跟车、强行并线、偏离车道和超车（Shashua 等人，2018）。

迄今为止，对RSS模型的安全性表现的测试尚未包含使用真实驾驶数据创建的场景。以往的研究通过模拟自定义的危险测试场景来进行RSS评估工作，其中周围车辆的运动学参数（例如初速度和减速度）被设定为常数（李等人，2018；Zhao et al., 2019）。然而，近年来微观数据采集方法（如自然驾驶研究（NDS））的技术进步使得能够在真实驾驶中观测到安全关键场景。在NDS中，车辆配备车载数据采集系统（DAS），可在日常驾驶过程中持续记录视频数据和车辆运动学信息。DAS所收集的丰富且高精度的数据使得提取安全关键事件（SCEs）成为可能。NDS数据中包含的详细信息，如道路环境、车辆运动和驾驶员行为，对于在仿真平台中重建用于测试RSS模型的安全关键事件至关重要。

因此，本研究提出使用真实驾驶数据来评估RSS的性能。然而，在初步实验中发现，RSS安全距离对参数集较为敏感。每个参数的微小变化都会导致RSS安全距离的不同计算结果，从而产生完全不同的自动驾驶决策策略。因此，有必要探究在合理边界内是否存在一组最优参数，使RSS模型能够实现最佳安全性表现，以充分挖掘RSS在提升自动驾驶车辆安全性方面的潜力。为此，本研究以识别这些最优参数并基于真实驾驶数据开发测试场景为双重目标，利用来自上海自然驾驶研究（SH‐NDS）中安全关键事件（SCEs）提取的模拟安全关键跟车场景，对RSS模型进行了校准和测试。本研究的方法与流程如下：1）采用触发方法并结合人工验证，从 SH‐NDS数据中提取跟车场景下的安全关键事件；2）将这些跟车SCEs转换为仿真平台中的安全关键场景，并将人工驾驶的试验车辆替换为嵌入RSS模型的自动驾驶车辆；3）校准RSS，确保自动驾驶车辆在所有场景下均能实现最佳安全性表现；4）通过比较嵌入 RSS的ACC、仅ACC以及无辅助的人类驾驶员的表现，验证校准后的RSS模型所带来的安全性提升。

2. 文献综述

2.1. 安全性关键事件的识别

安全性–关键事件（SCE）是指目标车辆必须采取快速避险操作以避免发生碰撞的情况，即可能以碰撞或接近碰撞告终的事件。制动是最常见的避险操作或紧急措施。根据弗吉尼亚理工学院100辆车自然驾驶研究，丁古斯等人（2006）发现驾驶员在超过80%的安全关键事件中会执行制动操作；因此，异常的纵向减速度（例如大于− 0.5 重力加速度单位g）已被证明是识别安全关键事件最有效的指标。大多数先前的研究通过以下两个步骤从原始自然驾驶数据中识别有效的安全关键事件：1）设置车辆运动学触发器，2）人工验证由运动学触发器提取出的事件视频。现有文献中使用的触发标准摘要见表1。

需要注意的是，已有若干研究应用机器学习算法（例如图像识别、随机森林）来检测自然驾驶数据中的安全关键事件。与触发方法相比，这些算法将误报率控制在相对较低的水平，但同时漏报率几乎增加了20%（Dozza 和 Gonz´ález，2013；高等人，2018）。

为避免样本中丢失近20%的安全关键事件，本研究采用了触发方法进行安全关键事件的识别。

2.2. 责任敏感安全

已有研究对RSS模型进行了测试和改进。在跟车场景方面，李等人（2018）旨在弥补原始RSS模型在确定安全间距时的保守性，因为车辆选择过大的间距可能导致交通流效率降低。’研究人员对该模型进行了修改，使其适应三种不同的跟车状态：跟随、离开和接近，其中接近状态与本研究中的安全关键跟车场景类似。李等人（2018）的研究结果表明，应用多状态模型有助于减小所需的安全间距，从而更有效地利用道路资源。–赵等人（2019）提出了一种路权分配策略以提升RSS模型在变道场景中的性能。’具体而言，将路权协商阶段融入原始的RSS变道策略中，并定义了禁止区域和协商区域以支持自动驾驶车辆的决策。该新策略能够提高车辆间通信的效率，并增强对有限道路资源的利用。’

然而，现有RSS文献存在两个不足之处。第一，RSS模型的参数值是凭经验设定的，有必要探索一组能更好地平衡安全性表现与道路资源利用的参数集。第二，在仿真测试中，周围车辆的速度和加速度被设为常数，无法完全反映真实的驾驶环境。本研究通过基于自然驾驶数据对标定和测试RSS模型，解决了上述两个问题。

2.3. 自适应巡航控制

当当前情况不满足自动驾驶车辆所定义的安全距离时，RSS模型可为自动驾驶车辆提供适当的制动策略，但还需要第二种算法来支持RSS未激活时自动驾驶车辆的更常见决策。自适应巡航控制（ACC）算法就是此类算法之一。ACC借助车载传感器的反馈，帮助车辆自动响应前车驾驶行为的变化并保持安全距离（范德海登等人，2018）。研究表明，ACC在增强交通流稳定性、提高驾驶舒适性以及减少交通事故方面具有显著效果（里格等人，2005；马格迪奇和阿尔托夫，2017）。

然而，在前车紧急制动等危险情况下，自适应巡航控制需要显著更长的车头时距，导致自动驾驶车辆行为过于保守（普洛格等人，2013）。Milan´es 等人（2014）模拟了中等拥堵交通流中反复发生减速度的真实驾驶场景，并分析了配备自适应巡航控制车辆的速度曲线。结果表明，自适应巡航控制往往产生响应延迟和不舒适的制动。其他研究也得出了类似结论，即基于传统跟车控制器（如智能驾驶员模型（IDM））建模的ACC系统会导致车辆运动学不稳定（Milan´es 和 Shladover，2014；苏等人，2016）。

先前的研究表明，当前方车辆行为引发突然的驾驶波动时，自动驾驶车辆的ACC系统在感知和响应方面尚不足以达到理想效果。

正是这种缺陷，结合ACC系统的总体有效性，使其成为本研究的理想第二算法。它能够有效支持自动驾驶车辆的常规决策，同时其缺陷可通过集成RSS模型得到改善。

该秒的目的之一 研究旨在确定最优参数。自适应巡航控制设计参数，如期望时间间隔，必须假设用于诸如本研究中使用的 MATLAB Simulink 等仿真平台。采用了 MATLAB 模型预测控制工具箱TM 用户’指南 R2019a（ Bemporad 等，2019）中的参数，并回顾了其他文献以确保所采用的参数值为最广泛使用的值。参数如表2所示，但需注意，一些仅提供了期望时间间隔Tgap参考范围的研究未列出。同样需要注意的是，本研究中应用的 1.5秒 值满足相关文献中提到的所有范围（ ISO 15622，2018；Milanes等人，2014；Makridis等人，2018）。

2.4. 替代安全指标

本研究需要采用合适的替代安全指标（SSM）来评估自动驾驶车辆（AV）算法的安全性表现。由于碰撞事件相对罕见，替代安全指标（SSM）具有实用性，因其不仅考虑碰撞，还涵盖接近碰撞的情况。替代安全指标（SSM）能够建立与碰撞风险和微观车辆运动学之间的关联，并在一定程度上反映发生碰撞的概率（李等人，2017a,b）。以往的研究中已采用多种指标作为替代安全指标（ SSM），例如车头时距（Vogel，2003）、避免碰撞的减速度率（Meng和Weng，2011）以及碰撞时间（TTC）（Kiefer等人， 2005；Oh和Kim，2010；Meng和Qu，2012）。在这些替代安全指标（SSM）中，TTC客观且被广泛使用。它基于时间接近性，综合了空间接近性和速度差（Zheng等人，2014；Mahmud等人，2017）。先前的研究表明，TTC是识别交通冲突的有效指标，冲突事件中出现的最小TTC可直接用作衡量冲突严重程度和碰撞风险的依据（Gettman和Head，2003；Oh和Kim，2010）。

Morando等人（2018） 观察到，在涉及人工驾驶车辆的冲突（人对人及人对自动驾驶车辆）中，当TTC小于或等于1.5秒时，可能导致潜在的不安全情况。Gettman等人（2008） 进一步根据最小TTC将需要异常减速的冲突事件划分为三个严重等级：低度（1.0 秒 ≤ TTC ≤ 1.5 秒）、中度（0.5 秒 ≤ TTC ≤ 1.0 秒）和高度（TTC ≤ 0.5 秒）。

然而，TTC是一个瞬时值。TIT（时间积分TTC）是一种累积指标，用于评估TTC低于某一阈值的持续时间，反映一段时间内的追尾碰撞风险。现有文献中采用的该阈值（记为TTC*）在2至4秒之间变化（Minderhoud和Bovy，2001；Sultan等人，2002；Li 等人，2014；Mahmud等人，2017）。先前的研究表明，使用不同的TTC阈值在评估安全性效果时不会产生显著差异。Shi等人（ 2018）应用TIT来评估事故前的风险状况。当6个从1.5秒到4秒不等的TTC*值被

3. 数据准备

3.1. 安全关键事件提取

上海自然驾驶研究（SH‐NDS）是中国首个自然驾驶研究，由同济大学、通用汽车公司和弗吉尼亚理工交通研究所合作开展。共有57名驾驶员参与了该研究，其中包括45名男性和12名女性，年龄介于25至59岁之间，驾驶经验从1年至23年不等。参与者车辆配备了先进的数据采集系统，包括四个摄像头视角（向前、面部、手部、后向）、全球定位系统（GPS）、速度表、三维加速度计和雷达。

为期三年的SH‐NDS数据收集工作始于2012年12月，结束于2015年12月。该研究共收集了19,133次行程的数据，总行驶里程达 161,055公里。

SH‐NDS中收集的丰富运动学和视频数据—安全关键事件（SCEs）的有效提取。安全关键事件通常以异常的车辆运动学特征为标志，例如高横向和纵向加速度以及低碰撞时间（TTC）。在本研究中，初始的运动学触发标准参照了100辆车自然驾驶研究（丁古斯 等人，2006年），随后进行了轻微调整，以平衡误报率和漏报率。有关SCE提取过程的更多细节可参见我们之前的工作（王和徐， 2019），但最终的标准如下：
- 触发条件1：横向运动大于或等于0.7g；
- 触发条件2：纵向减速度大于或等于− 0.5g；
- 触发条件3：驾驶员在发生其认为关键的事件时按下仪表盘按钮，从而激活事件记录；
- 触发条件4：横向运动大于或等于0.5g，并且前向TTC小于或等于4秒；
- 触发条件5：纵向减速度大于或等于− 0.45g，并且前向TTC小于或等于4秒。

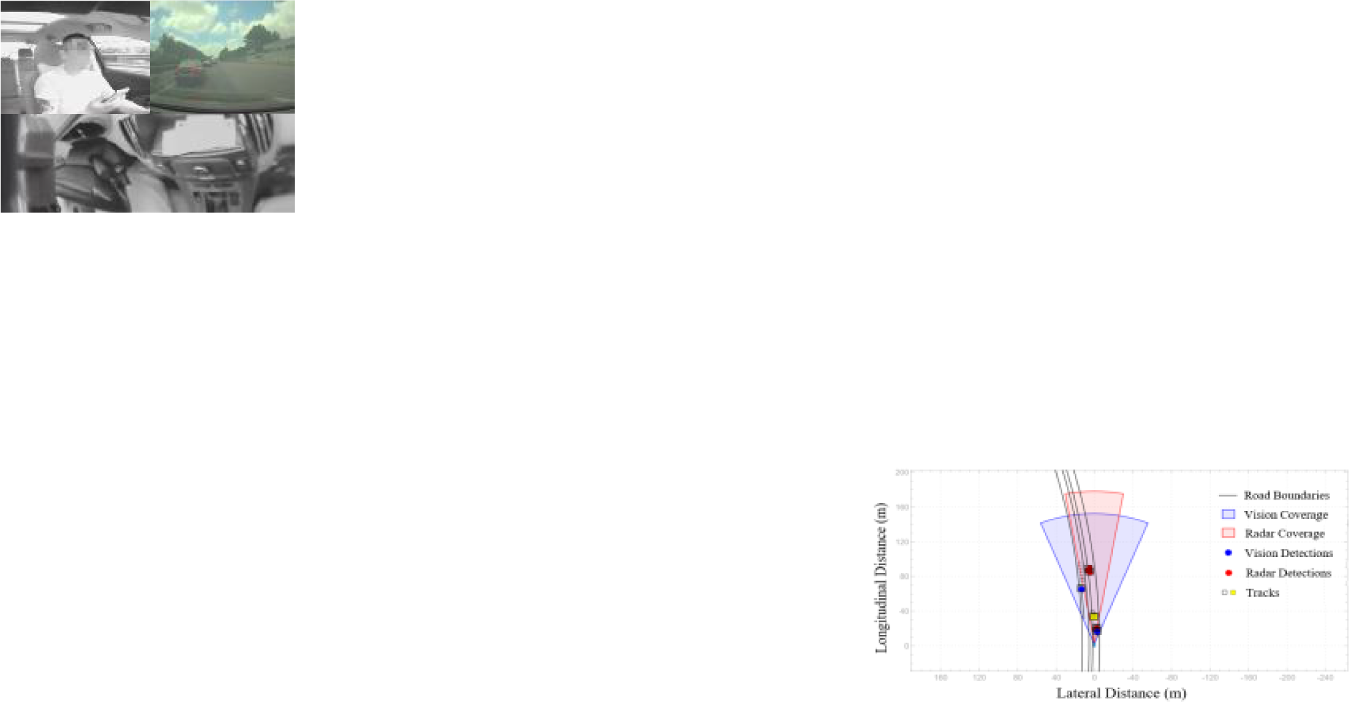
通过组合触发条件和人工验证，最终识别出591个安全关键事件，包括583个接近碰撞和8个碰撞。（见图1）

3.2. 安全性关键跟车事件分析

视频的人工验证显示，在591个安全关键事件中，有249个是由跟车场景中与前车（LV）发生冲突引起的。这类冲突在所有冲突类型中占比最高（42%）；作为参考，在100辆车自然驾驶研究中（丁古斯等人，2006年），与前车的冲突占48%（395/830），而在美国高速公路安全管理局’的两车碰撞前场景中占34%（纳吉姆等人，2007年）。由于此类事件发生频率较高，本研究选择了跟车安全关键事件进行分析。每个事件均在触发时刻前5秒至触发时刻后10秒的15秒时段内进行分析。在249个事件中，有26个因传感器对前车丢失超过10秒而被剔除，导致几乎无法追踪前车’的轨迹，进而难以进行后续的虚拟场景转换。剩余的223个安全关键事件中包含一次碰撞。这223个安全–关键跟车事件的环境条件，包括路面、天气、光照条件和道路类型，汇总于图2。

223个事件周期的车辆运动学分布以直方图和累积分布（红线）的形式显示在图3中。SV表示被试，即SH‐NDS车辆。SV的平均最大减速度为’s − 0.62 g，初速度为

4. 方法论

本研究利用从223起安全关键跟车事件中构建的场景，通过将人类驾驶的被试车辆替换为由嵌入RSS的ACC控制的自动驾驶车辆，对RSS模型进行了标定。我们的目标是找到RSS参数的最佳组合，以确保嵌入RSS的ACC在223个模拟跟车场景中实现最佳安全性表现。

4.1. 仿真平台

使用MATLAB中的自动驾驶系统工具箱TM创建了虚拟自动驾驶车辆和场景。场景创建所需的信息包括自动驾驶车辆的初始位置和速度、前车轨迹、道路中心和道路宽度。道路边界由工具箱自动推断，其余信息来自自然驾驶数据。

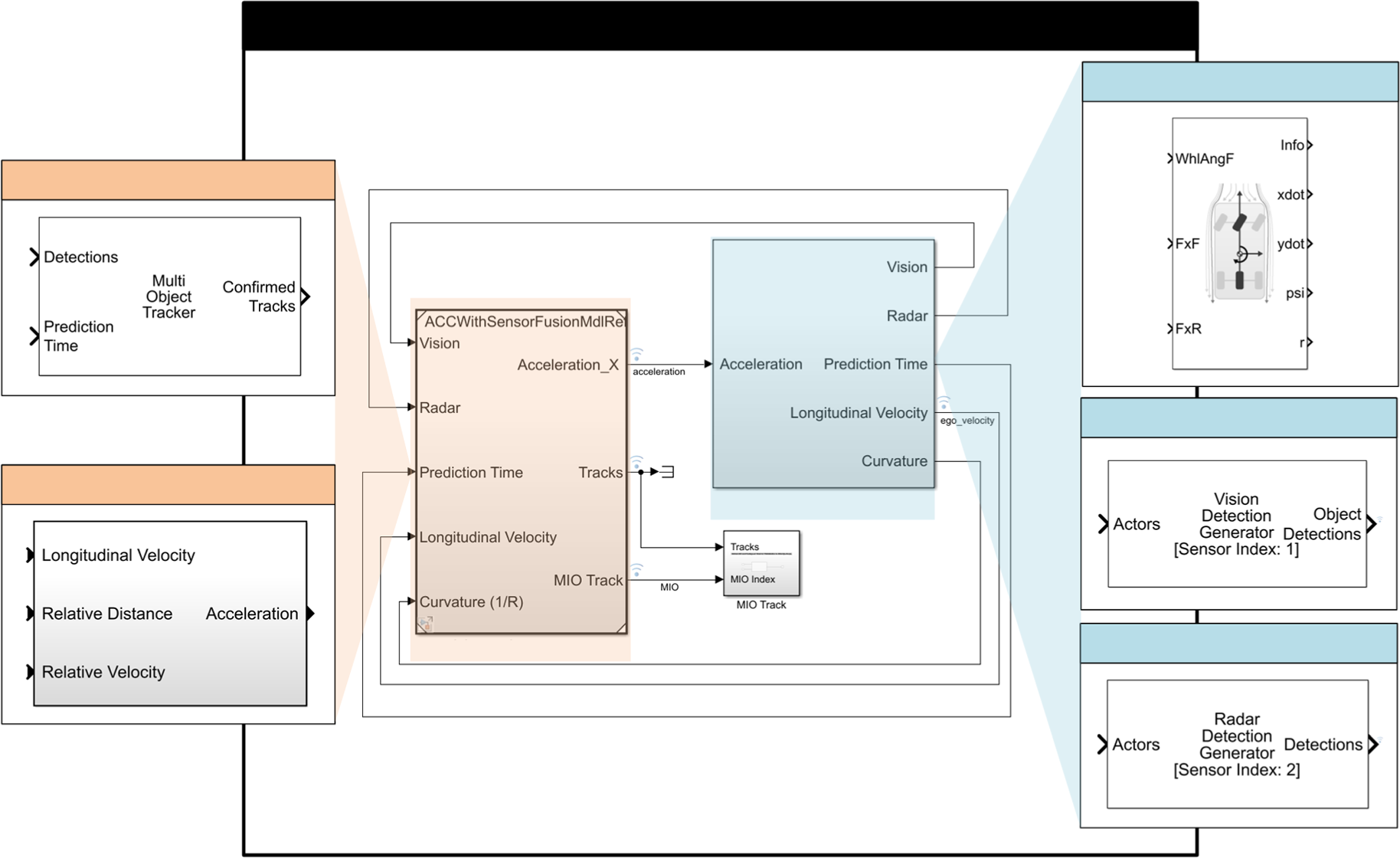
自动驾驶车辆的控制算法在MATLAB Simulink中实现。图4 展示了在Simulink中设计用于实现自适应巡航控制和责任敏感安全模型功能的模块。带RSS的ACC 模块负责将传感器信号处理为具有实际意义的数值（来自周围车辆的相对距离和速度），并根据自动驾驶车辆的当前纵向速度、与前车的相对距离和相对速度来确定自动驾驶车辆的加速度。’加速度。 车辆与环境 模块负责根据 带RSS的ACC 模块提供的加速度输入，计算车辆动力学和运动状态，同时检测驾驶环境中的物体和车辆，并向 带RSS的ACC 模块输出传感器信号。自行车模型用于建模车辆动力学系统。

4.2. 自动驾驶车辆控制算法

本研究中，测试的自动驾驶车辆由嵌入RSS的ACC进行控制。通过ACC算法，自动驾驶车辆使用模型预测控制（MPC）来保持与前车的

8.97 m/s；前车的平均最大减速度为− 0.67 g。被试车辆与前车的平均距离和初始相对速度分别为11.96 m和− 0.6 m/s（负号表示被试车辆速度更大）；平均最小TTC为1.31 s。

4. 方法论（续）

4.2. 自动驾驶车辆控制算法（续）

安全距离（范德海登等人，2018；普洛格等人，2013）。安全距离 $d_{safe}$ 定义如下：

$$
d_{safe} = d_{default} + T_{gap} \times V_x \quad (1)
$$

其中，默认间距 $d_{default}$ 和时间间隔 $T_{gap}$ 是自适应巡航控制的设计参数，分别设置为 5 米 和 1.5 秒；$V_x$ 表示自动驾驶车辆的纵向速度。考虑到自动驾驶车辆的运动能力，其纵向加速度被约束在 $[-3, 2]$ m/s² 之间。基于模型预测控制的自适应巡航控制算法通过求解一个有约束的优化问题来控制自动驾驶车辆的速度 $V_x$，以确保与前车的相对距离（$d_{relative}$）大于前方安全距离（$d_{safety}$）：

$$
\text{minimize } |V_x - V_{set}|^2 \
\text{subject to } d_{relative} - d_{safety} \geq 0 \quad (2)
$$

其中设定速度 $V_{set}$ 为设计参数，设定为 21.5 m/s。

对于责任敏感安全算法（RSS算法），其核心思想是：如果自动驾驶车辆（AV）与前车（LV）之间的纵向距离满足以下条件，则认为该距离是安全的：即使前车突然施加全力制动（$a_{max,brake}$），自动驾驶车辆在其响应时间（$\rho$）内以最大加速度（$a_{max,accel}$）加速，随后立即以至少最小合理制动力（$a_{min,brake}$）进行刹车，仍能避免碰撞，同时不会给乘客带来严重不适。最小安全纵向距离 $d_{min}$（类似于自适应巡航控制中的 $d_{safe}$）被计算为自动驾驶车辆速度 $v_a$、前车速度 $v_l$ 以及响应时间、最大加速度、最小和最大制动力（或减速度）等参数的函数。

$$
d_{min} = \left[ v_a \rho + \frac{1}{2} a_{max,accel} \rho^2 - \frac{(v_a + \rho a_{max,accel})^2}{2 a_{min,brake}} + \frac{v_l^2}{2 a_{max,brake}} \right]^+ \quad (3)
$$

其中 $[x]^+ = \max{x, 0}$；$\rho$，$a_{max,accel}$，$a_{min,brake}$ 和 $a_{max,brake}$ 为待标定的四个参数；$a_{max,accel}$ 为正值，而 $a_{min,brake}$ 和 $a_{max,brake}$ 为负值。

本研究基于以下策略将RSS模型集成到ACC系统中：1）在每个仿真步长，雷达传感器检测与前车的相对距离（$d_{relative}$）；2）同时计算RSS最小安全纵向距离（$d_{min}$）；3）如果 $d_{relative}$ 小于 $d_{min}$，自动驾驶车辆以最小减速度（$a_{min,brake}$）进行减速。否则，自动驾驶车辆由ACC算法控制。

4.3. 用于标定RSS模型的多目标函数

本研究旨在确保校准的RSS模型能够实现其最佳安全性表现的目标；即在将自动驾驶汽车算法应用于所有安全关键时段创建的场景后，目标是生成最低的时间积分TTC（TIT）。同时，应考虑模型的保守性，以防止其产生过大的相对距离。因此，多目标函数定义为：

$$
\Omega = (\max f_{Safety}, \min f_{Conservativeness})
$$

子目标一

$$
\max f_{Safety} = \min \sum_{i=1}^{N} TIT_i \
\sum_{i=1}^{N} TIT_i = \sum_{i=1}^{N} \sum_{t=1}^{T} [TTC^ - TTC_i(t)] \cdot \tau_{SC} \quad \forall 0 \leq TTC_i(t) \leq TTC^ \quad (4)
$$

其中，$N$ 是从自然驾驶数据中提取的安全关键跟车事件的总数，即 223。$TIT_i$ 以 s² 为单位，表示第 $i$ 个安全关键时段的 TIT 值，用于衡量安全性；$TTC^*$ 是 TTC 阈值，设定为 4 秒；$TTC_i(t)$ 表示在仿真步长 $t$ 时第 $i$ 个时段的 TTC 值；而 $\tau_{SC}$ 是两个仿真步之间的时间间隔，在本研究中等于 0.1 秒。

子目标二：

$$
\min f_{Conservativeness} = \min \sum_{i=1}^{N} \Delta d_i \
\sum_{i=1}^{N} \Delta d_i = \sum_{i=1}^{N} [d_{min}(t^{rss} i) - d {relative}(t^{rss}_i)] \quad (5)
$$

其中 $\Delta d_i$ 表示第 $i$ 个时间段内的保守性度量；$t^{rss} i$ 表示在第 $i$ 个时间段内 $d {min}$ 首次大于 $d_{relative}$ 的时刻。具体而言，$d_{min}$ 相对于 $d_{relative}$ 越大，RSS模型越早被激活，并迫使自动驾驶车辆在 $a_{min,brake}$ 处减速，从而使得模型更加保守。因此，当 $d_{min}$ 大于 $d_{relative}$ 时，$\Delta d_i$ 随之增大。需要注意的是，如果不存在 $d_{min}$ 大于 $d_{relative}$ 的时刻，则 $\Delta d_i$ 将被设为 0。

4.4. 校准方法

遗传算法（GA）被广泛用于寻找模型的’最优参数组合。GA能够求解有约束和无约束的全局优化问题，同时避免陷入局部最小值（朱等人，2018；赛富扎曼等人，2015），并可处理涉及不连续性、多模态、分离可行域以及噪声函数评估的复杂问题。然而，传统 GA 难以有效处理多目标优化问题，尤其是当各个目标函数之间存在冲突条件时。精英非支配排序遗传算法（NSGA‐II）已被广泛采用以解决此类多目标问题（德布等人，2002）。NSGA‐II’的优势在于：（1）引入快速非支配排序以降低计算复杂度；（2）采用精英策略以提升通用性能，并在进化过程中保留精英个体；以及（3）用拥挤距离比较法取代原始NSGA中的共享函数法，从而无需调整共享参数，同时保持种群多样性。

NSGA‐II的流程如下：（1）随机生成初始种群，种群中的每个个体对应RSS模型中的一个随机参数集；（2）对随机选择的个体对（父代）进行交叉操作，并对随机选择的个体进行变异操作，以生成子代个体；（3）将父代和子代合并；（4）通过快速非支配排序算法计算每个个体的适应度；（5）基于拥挤距离的计算进行选择；（6）获得下一代；（7）重复步骤2至6，直到满足停止准则。

本研究使用了MATLAB中的遗传算法工具箱。RSS校准的GA参数设置如下：种群大小300，最大代数300，停滞代数100。当满足以下任一条件时，校准过程终止：（1）在停滞代数内适应度函数值的平均相对权重变化小于函数容差（本研究中为10⁻⁶）；或（2）迭代次数达到最大代数。（参见图5）

5. 结果

5.1. 责任敏感安全模型参数的估计值

使用NSGA‐II算法对RSS模型进行了标定。需要注意的是，四个参数（响应时间、最大加速度、最小减速度和最大减速度）的边界作为优化问题的约束条件。上下限的定义考虑了以下原则：

(1) 所有参数均不应超过车辆动力学的限制。本研究在223起事件中最大减速度率的5%百分位数（图3中的‐0.8 g）作为 $a_{max,brake}$ 的下限。

(2) RSS模型中自动驾驶车辆的响应时间 ($\rho$) 与现有文献中的响应时间、感知‐反应时间和时间延迟概念一致，均指跟车场景中前车制动开始与自动驾驶车辆制动开始之间的时间间隔（王等人，2016；朱等人，2020）。表3列出了以往研究中仿真研究所采用的自适应巡航控制系统响应时间的汇总。参考文献中所应用的响应时间，本研究在校准过程中设定自动驾驶车辆响应时间的边界为 [0.1, 0.5] s，约为人类驾驶员的一半。

(3) 在安全关键事件中，自动驾驶车辆的减速度 ($a_{min,brake}$) 不应大于人类驾驶员的最大减速度，因为RSS旨在使自动驾驶车辆处于更安全、更舒适的驾驶状态。如图3所示，上海自然驾驶研究目标车辆的最大减速度最低值为− 0.4 g；因此，$a_{min,brake}$ 的上限被设定为− 4 m/s²。

多目标优化问题的解集，即帕累托前沿，如图6所示。帕累托前沿是参数空间中具有非劣解适应度函数值的一组点。换句话说，对于帕累托前沿上的每个点，只能通过降低另一个适应度函数来改进其中一个适应度函数。

由NSGA‐II算法生成的帕累托前沿包含105组参数集。由于本文主要关注自动驾驶车辆的安全性，因此选择了在子目标一（见公式(5)）中产生最低值的参数集。根据帕累托前沿的定义，没有其他参数集能够在子目标一达到相同低函数值的同时，在子目标二中获得更优的适应度函数值。换句话说，所选的参数集在具有相同保守性程度的参数集中实现了最佳的安全性表现，同时在产生相同安全性程度的参数集中是最不保守的。各参数的估计值及相应的目标函数值如表4所示。

如表4所示，子目标一的函数值为258.31 s²，表明在自动驾驶车辆参与的223个安全关键跟车场景中，所选参数组合能够在所有105个帕累托前沿参数集中产生最低的TIT总和；同时，由于将子目标二纳入多目标函数，RSS模型不会过于保守。校准的RSS模型定义的最小安全距离如下：

$$
d_{min} = \left[ 0.458v_a + 0.251 + \frac{(v_a + 0.978)^2}{4.272} - \frac{v_l^2}{15.250} \right]^+ \quad (6)
$$

5.2 校准RSS模型的安全性能

在Simulink中创建的安全关键场景下，测试了由嵌入校准RSS模型的自适应巡航控制（RSS‐embedded ACC）所控制的自动驾驶车辆（AV）。结果与原始自然驾驶研究事件中人类驾驶员的表现（无辅助的人类驾驶员）以及仅由ACC控制的自动驾驶车辆（ACC‐only）进行了比较。总体而言，自然驾驶研究数据中的223个安全关键事件（SCEs）包含1次碰撞，而ACC‐only和 RSS‐embedded ACC的模拟碰撞次数分别为22次和0次。由于RSS‐embedded ACC情况下未发生任何碰撞，进一步分析了TIT和最小TTC，以通过衡量潜在碰撞概率来评估自动驾驶车辆的安全性。

5.2.1 时间积分TTC（TIT）

图7 展示了TIT分布与人类驾驶员相比，自动驾驶车辆（仅ACC和嵌入RSS的ACC）的分布情况。横坐标表示按自动驾驶车辆与人类驾驶员之间TIT差异排序的223起事件，纵坐标表示自动驾驶车辆（蓝色点）和人类驾驶员（黑色点）的TIT值。连接各点的垂直线表示自动驾驶车辆与人类驾驶员TIT之间的差异程度，其颜色表示哪一方更大。具体而言，绿色表示人类驾驶员的TIT超过自动驾驶车辆的事件，即 TIT减少事件；红色表示TIT增加事件。

如图7a所示，对于仅ACC，TIT减少事件（119起）和TIT增加事件（104起）的数量相近。另一方面，嵌入RSS的ACC的TIT减少事件总数（如图7b所示的223起事件中的163起）明显多于TIT增加事件，这意味着嵌入RSS的ACC应能消除更多的安全关键事件。这一结论得到了所有事件TIT平均值的支持，人类驾驶员、仅ACC和嵌入RSS的ACC的TIT平均值分别为4.37秒、4.93秒和2.65秒：需要注意的是，仅ACC的TIT平均值为4.93秒，实际上比人类驾驶员的4.37秒均值表现出更低的安全性。两种自动驾驶车辆模型（仅 ACC和嵌入RSS的ACC）的TIT平均值在表5中被分别划分为TIT减少型和

表4 NSGA‐II算法生成的参数估计汇总。

参数（单位）	描述	边界	估计值	子目标1（s²）	子目标2（米）
$\rho$(s)	自动驾驶车辆的响应时间	[0.1，0.5]	0.458	258.31	4452.05
$a_{max,accel}$(米/秒²)	自动驾驶车辆的最大加速度	[1, 3]	2.389
$a_{min,brake}$(米/秒²)	自动驾驶车辆的最小合理制动力	[‐4, − 1]	− 2.136
$a_{max,brake}$(米/秒²)	有人驾驶车辆的完全制动力	[‐8, − 5]	− 7.625

表5 仅ACC与嵌入RSS的ACC的平均TIT与人类驾驶员TIT的对比，按TIT减少型和TIT增加事件分类。

	TIT减少事件		TIT增加事件
	人类	AV	人类	AV
仅ACC	5.175秒²	2.116秒²	3.457秒²	8.153秒²
嵌入RSS的ACC	4.754秒²	0.922秒²	3.340秒²	6.820秒²

TIT增加事件。可以看出，对于TIT减少事件，嵌入RSS的ACC将人类平均TIT从4.754秒²降低至0.922秒²，相比仅ACC（从5.175秒²降低至2.116秒²）实现了更大的降幅，表明嵌入RSS的ACC在降低潜在风险方面更具能力。

5.2.2. 最小TTC

除了TIT之外，最小TTC是本研究中另一个被调查的替代安全指标，因为它能更直观地反映交通冲突严重性。TTC小于或等于1.5秒被认为表示可能存在不安全的冲突（Morando et al., 2018；Gettman et al., 2008）。图8 显示了在人类驾驶员、仅ACC和嵌入RSS的ACC控制下，TIT减少型和TIT增加事件中的最小TTC分布情况。表6 列出了平均值。可以看出：

(1) 对于TIT减少事件，仅ACC和嵌入RSS的ACC均将人类驾驶员的平均最小TTC从低于1.5秒（分别为1.268秒和1.327秒）提高到了2.347秒和3.569秒，表明自动驾驶车辆成功缓解了潜在的不安全冲突。

（2）对于TIT增加事件，仅ACC的最小TTC集中在0秒至1秒之间，平均值为0.435秒，而人类驾驶员的最小TTC集中在1秒至2秒之间，平均值为1.348秒。与仅ACC类似，嵌入RSS的ACC的最小TTC也集中在0秒至1秒之间，但平均值较高，为0.495秒，而人类驾驶员的最小TTC集中在1秒至2秒之间，平均值为1.247秒。无论是仅ACC还是嵌入RSS的ACC，在TIT增加事件中均增加了冲突严重性，未能提升自动驾驶车辆相对于人类驾驶员的安全性。

5.2.3. 影响因素分析

Taking human drivers as a benchmark，建立了二元逻辑回归模型以探讨显著影响自动驾驶车辆’提升安全性的能力的解释变量，即场景相关因素。事件 $i$ 的因变量是二元变量 $y_i$，假设其服从伯努利分布。该变量定义如下：

$$
y_i = \begin{cases}
1 & \text{TIT- reduced events} \
0 & \text{TIT- increased events}
\end{cases} \quad (8)
$$

$p_i$ 被定义为 $y_i$ 等于1的可能性。因此，逻辑回归模型如下所示：

$$
p_i = P(y_i= 1|X_i) = \frac{\exp(\alpha+ \beta X_i)}{1+ \exp(\alpha+ \beta X_i)} \quad (9)
$$

其中 $X_i$ 是事件 $i$ 的解释变量矩阵；和 $\beta$ 是回归参数向量。表7列出了本研究中的解释变量。基于这些变量，模型估算了自动驾驶车辆安全性表现优于人类驾驶员的概率；即自动驾驶车辆的TIT不超过人类驾驶员TIT的概率。采用向后消除方法对用于变量选择。针对仅ACC和RSS的两个逻辑回归模型的输出 -

嵌入式自适应巡航控制进行总结 d 在 表8中。可以看出：

(1) 对于仅ACC，前车平均速度和标准差对自动驾驶车辆的安全性提升有显著影响。具体而言，在前车平均速度较高且标准差较低的场景中，仅ACC的表现可能优于人类驾驶员。比值比（OR）表示连续变量每增加一个单位时产生TIT减少型事件的相对几率。因此，前车速度标准差的比值比（=0.579）表明，每增加1米/秒

表6 仅ACC和嵌入RSS的ACC在TIT减少型和TIT增加事件中的平均最小TTC。

	TIT减少事件		TIT增加事件
	人类	AV	人类	AV
仅ACC	1.268秒	2.347秒	1.348秒	0.435秒
嵌入RSS的ACC	1.327秒	3.569秒	1.247秒	0.495秒

标准差的增加将使仅ACC降低人类驾驶员TIT的概率几乎减半，这表明在前车速度波动的情况下，仅ACC的表现不如人类驾驶员。

(2) 对于嵌入RSS的ACC，初始相对速度和前车平均速度与自动驾驶车辆的安全性提升呈正相关，而前车加速度的均值和标准差则具有负向影响。由于相对速度等于前车速度减去自动驾驶车辆速度，较高的值表示前车速度较高，意味着相对距离在增加，因此情况更安全。初始相对速度的比值比（=1.241）表明，初始相对速度每增加1米/秒，优于人类驾驶员的相对几率将增加0.241倍（1.241–1= 0.241）。前车加速度的均值和标准差每增加1米/秒²，产生TIT减少型事件的概率分别降低至0.326倍和0.616倍，这表明在面对前车加速度波动时，嵌入RSS的ACC不如人类驾驶员。

(3) 尽管通过NSGA‐II估计的前车最大减速度（‐7.625 m/s²）低于在部分223个安全关键事件中观察到的最大值，但嵌入RSS的 ACC的逻辑回归模型表明，前车最大减速度并未显著影响其安全性提升效果，这意味着当遇到减速度更大的前车时，嵌入RSS的 ACC并未表现出明显的不适应性。事实上，在总共54个前车减速度超过− 7.625 m/s²的安全关键事件中，嵌入RSS的ACC在其中 40个事件中成功提升了整体安全性。

5.2.4. 运动学统计

Also compared among 人类驾驶员、仅ACC和嵌入RSS的ACC各自事件的运动学统计，包括目标车辆加速度、速度、相对速度和与前车的相对距离的均值和标准差。’ s kinematic statistics, including the mean and standard deviation of the subject vehicle ’ s acceleration, speed, relative speed, and relative distance from LV. Distributions of each event ’的运动学统计分布以箱线图形式在图9 中展示。

采用方差分析（analysis of variance）来检验三个组的均值之间是否存在显著差异

表7 二元逻辑回归中解释变量的描述性统计。

解释变量	仅ACC		嵌入RSS的ACC
	TIT减少事件	TIT增加事件	TIT减少事件	TIT增加事件
自动驾驶车辆的初速度（m/s）	10.06	7.73	9.96	6.30
初始距离（m）	12.62	11.20	13.39	8.07
初始相对速度（m/s）	− 0.71	− 0.48	− 0.55	− 0.73
前车最大减速度（g）	− 0.64	− 0.68	− 0.65	− 0.68
LV的平均加速度 (m/s²)	− 0.09	0.10	− 0.08	0.20
前车加速度标准差（m/s²）	2.43	2.85	2.44	3.13
LV的平均速度（m/s）	6.57	5.07	6.42	4.38
LV的速度标准差（m/s）	2.69	3.37	3.09	2.78

注：解释变量的值是相应事件类型（TIT减少型或TIT增加事件）的平均值。

表8 逻辑回归模型的输出。

模型	解释变量	β estimate	Sig.	比值比	95%比值比置信区间
					下限	上限
模型1：仅ACC	前车速度标准差	− 0.547	0.000 **	0.579	0.467	0.716
	前车平均速度	0.414	0.000 **	1.513	1.294	1.769
	常数	− 0.513	0.072	0.599	/	/
模型2：嵌入RSS的ACC	初始相对速度	0.216	0.035 *	1.241	1.015	1.516
	初始距离	0.047	0.109	1.048	0.989	1.111
	前车平均速度	0.312	0.000 **	1.366	1.172	1.592
	前车加速度标准差	− 0.485	0.001 *	0.616	0.458	0.827
	LV的平均加速度	− 1.120	0.002 *	0.326	0.162	0.659
	常数	0.496	0.351	1.642	/	/

注： 表示差异在0.05水平上显著； *表示差异在0.001水平上显著。

运动学统计值。 表9 中的结果表明，在加速度的均值和标准差方面，人类驾驶员、仅ACC和嵌入RSS的ACC三组中任意两组之间均存在显著差异。然而，在相对距离的均值和速度标准差方面，人类驾驶员和仅ACC均与嵌入RSS的ACC存在显著差异，但两者之间无显著差异。

综合图9中的箱线图和表9中的方差分析结果可以看出：

(1) 与人类驾驶员或仅ACC相比，嵌入RSS的ACC产生的加速度和速度均值更低，这意味着在嵌入RSS的ACC控制下，自动驾驶车辆经历了更多的减速阶段，以避免卷入潜在危险的交通冲突。

(2) 嵌入RSS的ACC实现了比人类驾驶员或仅ACC更大的相对速度和相对距离。由于相对速度衡量的是前车比后随车辆快多少，较大的相对速度和相对（跟车）距离均值表明，嵌入RSS的ACC为自动驾驶车辆提供了更宽松、更舒适的驾驶条件。同时，更大的相对距离意味着嵌入RSS的ACC比其他组更为保守，可能导致道路资源利用不足。

(3) 嵌入RSS的ACC的相对速度标准差显著小于人类驾驶员，其速度标准差也显著小于人类驾驶员和仅ACC，表明嵌入RSS的ACC能够提高自动驾驶车辆的速度稳定性。

5.2.5. RSS激活时刻

To further investigate the RSS模型’用于提升自动驾驶车辆安全性的机制，分析了每个事件中人类驾驶员和嵌入RSS的自适应巡航控制的加速度曲线。图10 展示了四个随机选取的TIT减少型示例事件的曲线。自动驾驶车辆’的期望加速度是自动驾驶汽车算法计算出的当前目标加速度/减速度，可以看出其与自动驾驶车辆’的实际加速度存在差异：由于车辆性能的限制，自动驾驶车辆’的实际减速度曲线略有延迟且有所变化。

RSS激活时刻定义为自动驾驶车辆’的期望减速度达到 $a_{min,brake}$ 的时刻，而人类反应时刻则是自然驾驶研究驾驶员开始刹车的时刻。

在图10所示的四起事件中，RSS分别比人类驾驶员反应时刻提前了1.0 s、1.7 s、2.0 s和2.6 s被激活’，这表明嵌入RSS的ACC模型比人类驾驶员提前1.0 s、1.7 s、2.0 s和2.6 s感知到了潜在的安全性–临界情况，因此通过提前制动更有效地降低了安全性–临界水平。对于163起TIT减少型事件，RSS平均提前制动时间为2.60 s，而对于全部223起事件，平均时间为2.31 s。

6. 讨论与结论

为实现对跟车场景中RSS模型的标定与评估，本研究利用从上海自然驾驶研究（SH‐NDS）中提取的223个有效的安全关键跟车事件（SCEs），在Simulink中进行场景复现。在虚拟场景中，由集成RSS的自适应巡航控制（ACC）控制的自动驾驶车辆（AV）替代了NDS中人工驾驶的试验车辆，该自动驾驶车辆继承了原目标车辆的初速度及与前车的距离。在自动驾驶车辆完成所有安全关键事件的仿真后，对RSS模型进行了标定，以实现最佳安全性表现。

RSS校准的多目标函数同时考虑了安全性和保守性。对于每个事件，安全性通过所有安全关键事件中累积的碰撞时间积分（TIT）来衡量，而保守性则通过RSS定义的安全距离（$d_{min}$）在首次小于相对距离（$d_{relative}$）时超出该相对距离的程度来衡量。如果不引入保守性这一子目标，校准结果将完全可预见：根据公式(3)，最终选择的最优参数集将是$\rho$、$a_{max,accel}$、$a_{max,brake}$的上限以及$a_{min,brake}$的下限，因为它们会生成最大的安全距离（$d_{min}$）；也就是说，更大的 $d_{min}$ 更优，因为它意味着自动驾驶车辆必须与前车保持更长且因此更安全的距离。然而，尽管安全性表现可能得到增强，但道路资源会被极度浪费。因此，为了在模型的安全性表现和保守性之间取得平衡，有必要求解该多目标优化问题。

因此，使用NSGA‐II算法对RSS模型进行了标定。帕累托前沿共包含105个参数集，最终选择了子目标一中取值最小的参数集，即实现最佳安全性表现的参数集。RSS模型的校准后的参数估计值如下：自动驾驶车辆的响应时间（$\rho$）0.458 秒，有人驾驶车辆的完全制动力（$a_{max,brake}$） − 7.625 米/秒²，自动驾驶车辆的最大加速度（$a_{max,accel}$）2.389 米/秒²，以及自动驾驶车辆的最小合理制动力（$a_{min,brake}$） − 2.136 米/秒²。

对人类驾驶员、仅ACC以及标定后的嵌入RSS的ACC的安全性表现进行了检验和比较。嵌入RSS的ACC能够将每次事件中的平均 TIT从人类驾驶员的4.37 s²降低至2.65 s²，而仅ACC则产生了相反的效果，使平均值增加至4.93 s²。对于嵌入RSS的ACC，TIT减少的事件比例为73.1%（163/223），比仅ACC高出近20%。仅ACC未能改善近50%安全关键事件的安全性表现：逻辑回归结果表明，在前车速度标准差较大的情况下，仅ACC无法提升安全性。这些结果与以往研究发现一致，即在交通流不稳定等异常驾驶条件下，ACC的可靠性不足（Milanes等人，2014；Milan´es和Shladover，2014；苏等人，2016）。推断嵌入RSS的ACC在60个事件中未能提升自动驾驶车辆安全性’的主要原因如下：1）自动驾驶车辆成功检测到相对距离未满足RSS安全距离的关键情况，但场景过于紧急，施加 $a_{min,brake}$ （‐2.136 m/s²）不足以有效降低碰撞风险；2）由于RSS安全距离方程未考虑速度差和加速度在形成危险情况中的作用，自动驾驶车辆未能及时检测到潜在的关键情况。根据图9 和 表9所示的运动学统计结果，嵌入RSS的ACC在

表9 运动学统计的方差分析结果。

因变量	(I) 组	(J) 组	均值差异 (I‐J)	标准误差	Sig.	99%置信区间
						下限	上限
加速度均值	人类	仅ACC	0.114*	0.043	0.024	0.011	0.216
	人类	带RSS的ACC	0.272*	0.037	0.000	0.183	0.361
	仅ACC	带RSS的ACC	0.159*	0.056	0.014	0.025	0.292
速度均值	人类	仅ACC	− 0.835*	0.347	0.016	− 1.517	− 0.153
	人类	带RSS的ACC	0.119	0.347	0.732	− 0.563	0.801
	仅ACC	带RSS的ACC	0.955*	0.347	0.006	0.273	1.637
相对速度均值	人类	仅ACC	− 0.409*	0.121	0.002	− 0.698	− 0.120
	人类	带RSS的ACC	− 0.622*	0.127	0.000	− 0.926	− 0.317
	仅ACC	带RSS的ACC	− 0.212	0.107	0.136	− 0.469	0.044
相对距离均值	人类	仅ACC	0.488	0.610	0.809	− 0.974	1.949
	人类	带RSS的ACC	− 3.121*	0.725	0.000	− 4.859	− 1.383
	仅ACC	带RSS的ACC	− 3.608*	0.715	0.000	− 5.324	− 1.893
加速度标准差	人类	仅ACC	− 1.654*	0.025	0.000	− 1.714	− 1