优化模拟滤波器降低质子声探测剂量

用于提高质子声探测器精度的模拟滤波器设计

摘要

本文分析了如何通过优化模拟信号处理环节，特别是模拟滤波器，来提高离子声技术质子射程验证的精度。离子声技术能够对质子束在水吸收体中的穿透深度/射程进行空间检测，在强子治疗过程中的实时束流监测方面具有潜在的临床应用价值。现有技术采用非优化的探测器，导致信号质量较低，因而需要更高的总剂量，这与临床应用不相容。基于此，本文将全面分析声信号带宽、信噪比以及噪声功率/带宽。同时讨论这些信号质量参数与可达到的最大质子射程测量精度之间的相关性。特别地，使用优化滤波器相比非优化滤波器方法，可将实现特定精度所需的剂量降低高达98.4%。

关键词 ：核成像；粒子加速器；粒子束测量；声波；模拟电路；数字电路

1. 引言

离子声学测程验证是一种有前景的方法，用于实验测量质子束在吸收体中的射程。当粒子射程末端的布拉格峰（BP）区域发生能量快速沉积时，会产生声信号，该信号可通过专用传感器采集，并通过测量声波的飞行时间来确定布拉格峰的位置。这一技术在肿瘤学强子治疗领域具有诸多潜在应用，相比目前使用的核成像技术（如正电子发射断层扫描（PET）、瞬发伽马射线成像），它有望实现更精确的实时定位[1–4]。提高布拉格峰定位精度可实现实时监测治疗过程，确保辐射剂量准确施加于目标治疗体积内。离子声技术最早由Sulak于1979年提出，而Hayakawa于1995年首次在患者体内观测到离子声信号[5,6]。

近年来，已在临床前（<65MeV）和临床（65至250 MeV之间）能量下开展了大量实验[7–13]。在临床前场景中，布拉格峰定位精度可达数万微米级别，在临床能量下则约为毫米量级。然而，该技术在临床场景应用中的最大障碍是实现上述精度所需的高剂量，这与临床治疗要求不相容。事实上，在临床场景中，声信号极其微弱（处于毫帕量级）。现有技术采用非优化的通用电子设备，限制了可达到的信噪比，因而必须依赖后处理方法（对多次束流脉冲的声信号进行平均法处理），这显著增加了沉积剂量。

因此，本文分析了使临床场景至关重要的主要方面，并展示了优化的模拟滤波器如何显著降低获得特定精度（定义为测量焦点区位置的标准偏差）所需的剂量。

本文组织如下：第2节介绍了文献中临床前和临床场景的特点，特别关注所使用的仪器设备以及达到的信噪比。第3节提出了离子声学实验的跨领域模型，并评估了影响测量精度的主要因素。第4节展示了优化的模拟滤波器如何显著降低剂量。最后，在第5节中得出结论。

2. 离子声学实验装置及场景

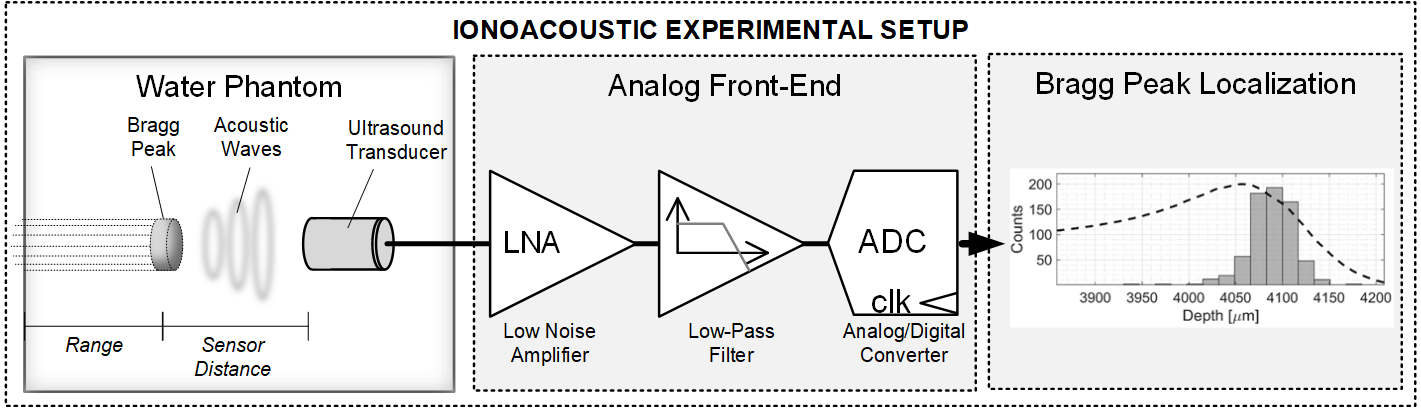
离子声学实验装置通常由脉冲粒子束流构成，该束流撞击水模体，在其中产生压力信号。随后，压力信号在水中传播，并由特定的声学传感器（AS）检测。信号被转换至电压域后，通过模拟前端（AFE）进行调理，并转换到数字域，在数字域中通过测量声波的飞行时间（ToF），确定焦点区（BP）相对于声学传感器的位置。典型的离子声学实验装置示意图如图1所示。

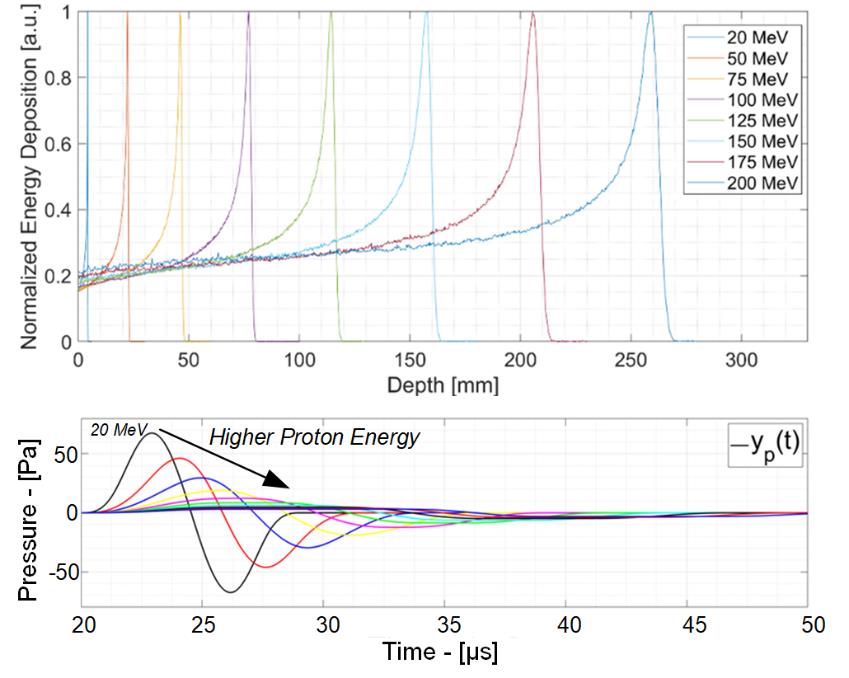
图2显示了布拉格曲线在不同束流能量下的变化情况。当处于亚临床能量时，射程仅为几毫米；而在临床能量下，射程可从几厘米到几十厘米不等，以到达位于不同深度的肿瘤。随着射程的增加，布拉格峰半高全宽 (焦点区FWHM) 和因此，布拉格峰体积相应增加。该体积确实不延伸线条随着能量的增加。因此，在高束流能量下，能量会下降。每单位假设质量单位（称为剂量，D）变低。由于预压的幅度确定信号是与剂量成正比，这意味着在临床前能量下压力标志在焦点区的压强为数十或数百帕斯卡，该值会下降到几帕或 P 的分数 a 在临床场景中，如图2底部所示。

考虑从焦点区到传感器的球面传播，在临床前场景中传感器获取的信号为几Pa，而在临床场景中该值下降到几毫帕斯卡。为了获取如此微弱的信号，现有技术通过严重依赖后处理算法（如平均法）来提高信号‐噪声比 (SNR)，以多次波束照射的方式实现。然而，这种信噪比的提升是以增加额外剂量为代价的。特别是在，th信噪比和剂量随平均法增加，如公式(1)和(2)所示，其中 SNR1sh 和 SNRavg 分别为单次照射，Nsh 为平均束流照射次数以及总剂量 Dtot 是单次照射剂量 D1sh 的 Nsh 倍。

$$
SNR_{avg} = SNR_{1sh} + 10 \log N_{sh} \tag{1}
$$

$$
D_{tot} = N_{sh} D_{1sh} \tag{2}
$$

增加布拉格峰体积的另一个影响是声信号频率的降低。特别是，20 兆电子伏特束流产生的信号主频率为 2 兆赫兹，而在临床能量下，该值下降到几十千赫兹。公式(3)显示了信号频率（fsignal）、水中声速 cW（30 摄氏度时为~1500米/秒）和布拉格峰半高全宽（BPFWHM）之间的关系。

$$
f_{signal} = \frac{c_W}{BPFWHM} \tag{3}
$$

质子束能量对频率的依赖性如图2（底部）所示。下一节将展示优化后的电离声探测器如何在保持相同精度的情况下减少额外剂量，突出探测器技术的进步如何使该技术更接近临床应用。

3. 影响电离声测量精度的因素

在文献中，探测器的精度通常是通过多次重复实验测量并观察收集的数据的方差来事后评估的。这种方法适用于评估达到的性能，但并未探究影响结果精度的因素。在缺乏信号特性与精度之间关系的精确信息的情况下，无法预先设计出能够实现特定期望精度的探测器。因此，本节研究了信号的主要特性与达到的精度之间的关系。向典型的电离声信号（双极脉冲）添加噪声。噪声具有给定信噪比和有限带宽。

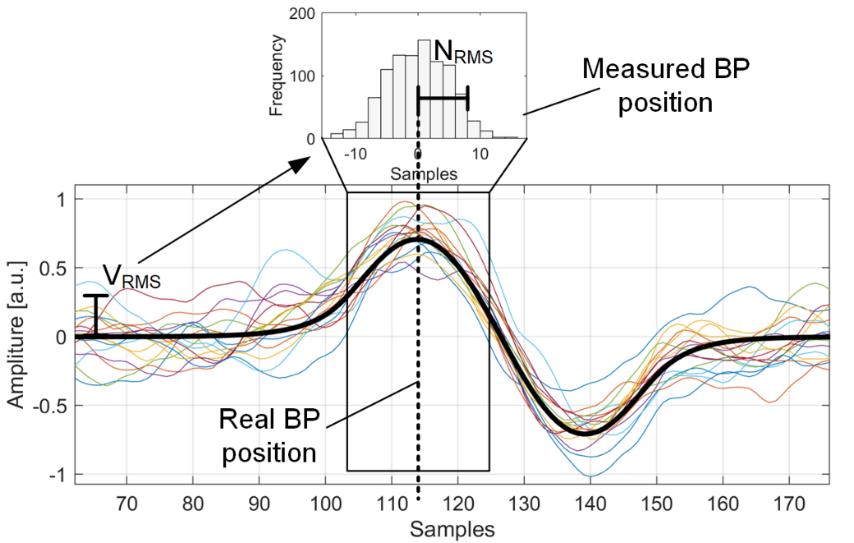
然后通过不同的噪声实现计算ToF，并通过评估ToF的方差来估计测量精度，如图3所示。接着评估三个不同参数对测量精度的影响。具体而言，这三个相关参数为信号频率、信噪比和噪声整形，其中噪声整形定义为信号带宽与噪声带宽的比率。

3.1. 信号频率

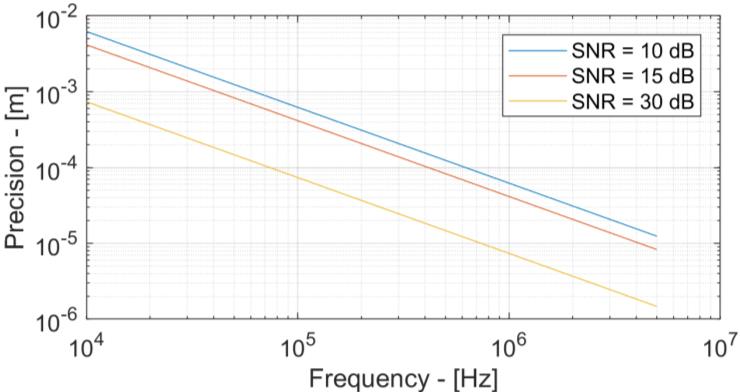
图4展示了在三个固定信噪比值下，测量精度对信号频率的依赖性。可以看出，随着信号频率的降低，精度以与1/f成正比的方式下降。当考虑到声学和光学系统中分辨率与波长之间众所周知的关系时，这种关系并不意外。然而，在离子声学实验中，这一效应解释了临床前和临床实验中性能差异的原因。特别是，在相同信噪比条件下，从20兆电子伏特束流（声信号为2兆赫兹）切换到200兆电子伏特束流（声信号为40千赫兹），将导致精度降低50倍。事实上，若在20兆电子伏特下10分贝信噪比可实现约10微米的精度，则在200兆电子伏特下相同的信噪比对应的精度仅为1.5毫米。同样地，对于50兆电子伏特束流（600千赫兹），要达到100微米的精度，15分贝信噪比已足够；而要使用150兆电子伏特束流（70千赫兹）达到相同精度，则需要30分贝信噪比。因此，临床场景不仅由于声信号弱而具有挑战性，还因为声信号的低频特性本质上损害了测量精度。

3.2. 信噪比

图5显示了在20兆电子伏特和200兆电子伏特两种情况下，精度与信噪比之间的关系。直观来看，在高信噪比下可实现的精度更高，但拥有一个能够量化该比率的分析工具，对于提取信噪比指标以设计达到期望精度的探测器至关重要。根据图4，由于信号频率的不同，20兆电子伏特下的精度高于200兆电子伏特下的精度。

为了验证本文所提出模型的结果，报告了精度结果 [13]已插入。事实上，本文报告了一项实验的精度结果 at 20兆电子伏特质子能量以及对信噪比的精确表征。它可以 s可以看出，此处提出 的模型与实验数据完全吻合。

最后，对数‐对数尺度下的线性趋势显示了精度与/SNRdB成正比。

3.3. 相对噪声带宽

除了信号频率和信噪比之外，还有一个对精度有重要影响的最终因素，那就是噪声的频率整形。事实上，这种应用 o低通滤波器会衰减高频噪声分量。这具有双重作用 e效应。首先，它提高了信噪比，降低了噪声功率。其次，减少高频的 f噪声的频率分量增加了相邻样本之间的相关性。在 f而白噪声（即在远大于信号带宽的带宽内具有平坦功率谱密度的噪声）是完全不相关的，在应用低通滤波器后 e消除了高 gh‐frequency comp分量并使噪声相关 为了分离信噪比和噪声频率整形的影响，我们引入了相对 a相对噪声带宽（RNBW），定义为噪声带宽BWnoise的比率 a和信号频率 .

$$
RNBW = \frac{BW_{noise}}{f_{signal}} \tag{4}
$$

对于较高的RNBW值，噪声带远高于信号的噪声带（白噪声，不相关）；而对于趋近于1的 RNBW值，噪声带始终更 s与信号（粉红噪声，相关）类似，如图6所示。为了 s隐式地，使用了一个二阶巴特沃斯低通滤波器，但更精确的 s可以通过改变滤波器的类型和阶数来进行研究。图7显示了在20兆电子伏特情况下不同RNBW值的影响。给定2兆赫兹的信号带宽，RNBW值从100（200兆赫噪声带宽，白色不相关噪声）变化到1 (相同的噪声和信号带宽）。值得注意的是，噪声带宽具有 a对精度有显著影响。例如，在信噪比为20分贝时，精度为 e在白噪声情况下（RNBW = 100）等于32微米，并可改善至6微米 i在RNBW = 1的情况下。这种影响可以通过考虑白噪声中的情况来解释， s后续样本之间几乎没有关联。我们称x M 为对应的样本

相反，在相关噪声（低频噪声）的情况下，相邻样本的值将相似（样本之间变化的统计值小于1西格玛），且变化发生在更大的时间尺度上。因此，更容易检测到真实最大点，从而在相同信噪比下提高精度。该影响突显了正确进行模拟滤波器尺寸设计的重要性，因其通过抑制高频噪声（提高信噪比）和使噪声相关来进一步提高精度。同样，模型结果与[14],高度一致，其中使用了RNBW为= 25的三阶巴特沃斯滤波器。

3.4. 电离声学相对精度

图8 包含并总结了前几节中显示的所有影响，可用作在任何场景下评估探测器性能的图表。事实上，纵轴（y轴）上报告的是相对于布拉格峰（BPFWHM）尺寸的相对精度，而非绝对精度。如第2节所述，BPFWHM 等于声信号波长的一半。因此，通过绘制相对精度，我们自动包含了图4 中所示信号频率的影响。因此，图8 是预测任何场景下测量精度的有用工具。特别是，图8 可用于推导任何实验场景的项目规格。例如，为了使用200兆电子伏特束流实现0.5毫米精度（相对于BPFWHM为2.5%）且在10毫帕0-peak传感器处的信号，图8显示，在等效噪声带宽为= 1时，需要达到17分贝信噪比。这意味着声学传感器的等效噪声必须比10毫帕低17分贝，即1毫帕RMS。通过这种方式，可以确定声学传感器的主要设计规格（共振频率和噪声底限）以及前端的主要设计规格（噪声系数、滤波器截止频率、模数转换器特性），以使探测器达到期望精度。

4. 200 兆电子伏特质子声探测器的模拟滤波器设计

第3节的结果表明，模拟滤波器是提高电离声探测器精度的基本环节。事实上，通过抑制带外噪声和干扰，模拟滤波器能够提高信噪比，从而提升精度，如图5所示。它还能衰减对精度有显著影响的高频噪声成分，如第3.3节所示。本节将应用前一节的结果，说明专用模拟滤波器如何改善电离声探测器的性能。

最坏情况场景已被考虑，对应于200兆电子伏特质子束，因为信号的低频和幅度使其更难实现高精度。该场景在文献中已有充分表征，典型特征如表1[7,10]所示。本节展示了针对此实验场景优化的二阶全差分劳赫低通滤波器设计，可实现RNBW= 1。该劳赫滤波器在给定频率$f_0 = 2\pi\omega_0$和品质因数Q处实现一对共轭复极点：

$$
\frac{V_{out}}{V_{in}} = \frac{\omega_0^2}{\omega_0^2 + \frac{\omega_0}{Q}s + s^2} \tag{5}
$$

参数	值
粒子束能量	200 兆电子伏特
每次照射的剂量	2 毫戈瑞
信号频率	13 kHz
布拉格峰处的信号幅度	200 毫帕
传感器处的信号幅度	2 毫帕
声学传感器距离	7.5 厘米
声学传感器灵敏度	4 毫伏/帕
声学传感器带宽	130 千赫
传感器噪声功率	4.5 µV RMS
传感器噪声功率谱密度	12 nV/√Hz
低噪声放大器通带增益	60 dB

滤波器方案如图9所示。

−3分贝频率（13 kHz）、品质因数（0.707，对应巴特沃斯滤波器）和增益（G = 1）可用于确定无源器件的元件值，如(6)–(9)[15]所示。主要滤波器参数和元件值列于表2中。

$$
R_1 = R_2 \cong \sqrt{\frac{IRN_{LPF}^2 - c \cdot IRN_{OpAmp}^2}{8kT(c + \sqrt{c})}} \tag{6}
$$

其中

$$
c = \left(1 + \frac{1}{G^2}\right)
$$

$$
R_3 = R_1 \cdot G \tag{7}
$$

$$
C_2 = \frac{1}{\omega_0 Q (R_2 + R_3 + G \cdot R_2)} \tag{8}
$$

$$
C_1 = \frac{1}{2 \cdot C_2 \cdot R_2 \cdot R_3 \cdot \omega_0^2} \tag{9}
$$

参数	值
−3 dB 截止频率	13 kHz
品质因数	0.707
输入参考噪声功率（0–13 kHz）	13 µV RMS
输入参考噪声功率谱密度 @13 kHz	100 nV/√Hz
相对噪声带宽（RNBW）	1
R1, R2, R3	44.2 kΩ
C1	294 皮法
C2	130 皮法

公式(5)允许对噪声源（运算放大器和电阻）进行设计，使其相对于传感器和低噪声放大器的噪声可以忽略不计。图10显示了模拟的低通滤波器频率响应。

5. 结果—模拟滤波器设计在200 MeV下的剂量减少

在最先进的实验中，很少关注滤波，其截止频率通常等于信号的10倍或更高（ RNBW > 10）。图11展示了前一节提出的最优滤波器（RNBW = 1）的影响，并可用于计算相对于现有技术的剂量减少。专用滤波器的影响如下：

• 噪声积分的频带受限于一个因子10，导致了噪声功率低 10 分贝，因此信噪比相应提高相同的量（图11的顶部）
• RNBW的减小使人们能够获得相同的测量精度（例如，0.5毫米 in the bottom of Figure 11) with an 8 分贝 lower 信噪比。

考虑到这两种结合的影响，使用优化滤波器相较于非专用的现有技术探测器，相当于实现了 18 dB 信噪比提升。

这种18 dB信噪比提升在考虑现有技术为达到优化滤波器性能所需额外剂量时尤为重要。事实上，现有技术提高信噪比的策略基于对束流多次连续照射进行平均。然而，平均法效率较低，因为噪声功率随照射次数的平方根而减小，而额外剂量则随照射次数线性增长。因此，为了匹配专用滤波器带来的18 dB信噪比提升，现有技术需要将束流照射63次，从而导致沉积剂量高出63倍。将这些性能与现有技术获得的性能进行比较，[7,10]分别报告在10 Gy和2 Gy剂量下实现了0.34 mm和2.2 mm的精度。使用专用模拟滤波器，可以将剂量显著降低至仅1.6%（1/63），分别仅需160 mGy和32 mGy即可实现相同的精度。

这一有希望的结果表明，离子声技术具有应用于临床场景的潜力，但也凸显出需要新一代专用电离声探测器。

6. 结论

本文展示了使用离子声技术进行质子射程测量时影响精度的主要因素。特别是，信号频率、信噪比和噪声带宽在设计新一代声学探测器时必须予以充分考虑。事实上，现有技术中的大多数实验旨在表征物理现象，使用的是通用电子设备，而非针对信号特性进行优化的设备。这导致需要大量后处理以在数字域中提高信号质量，但代价是额外剂量过高，无法满足临床应用的要求。本文表明，通过优化探测器尤其是模拟滤波器，可以显著降低剂量，从而使该技术更接近于临床应用。因此，下一代电离声探测器将需聚焦于优化且紧凑的仪器设备，而专用集成电路（ASICs）[14,15]的使用为此提供了可能。