基于耦合矩阵分割的滤波器设计

基于等效电路和耦合矩阵分割的先进滤波器设计技术

摘要

本文提出了一种利用等效电路分段技术高效设计通带波导微波滤波器的方法。该技术首先建立一个能够综合出期望传输函数的等效电路，然后通过对该等效电路进行分段，优化实际物理结构的不同部分。该技术最初是为同向滤波器开发的，而本文的主要贡献在于将该技术与耦合矩阵形式相结合。通过这种方式，我们首次将这种设计策略应用于复杂耦合拓扑结构的滤波器设计，突破了同向结构的限制。作为示例，采用全感性波导技术实现的一个复杂六阶双模滤波器，利用新提出的耦合矩阵分段技术进行了设计，验证了所提出理论的有效性。该滤波器的原型已被加工制造，并通过对实际原型的测量结果验证了该设计技术的精度。

关键词
电路分段，耦合矩阵，等效电路，微波滤波器，综合技术

1 引言

微波滤波器的设计对于地面和空间应用的各种通信系统的开发仍然是一项非常重要的工作。1,2由于滤波器响应对结构中的各个元件（谐振器和耦合元件）具有高度敏感性，这类器件的设计通常十分困难。这种高灵敏度使得优化技术不可靠，并且在实现最终期望响应的收敛时常常遇到困难。例如，在应用基于梯度的方法时，需要计算一个非常接近最终优化结构的初始结构。否则，这类方法通常会陷入局部最小值。3 ‐5

为了避免这一问题，进化算法也被用于滤波器优化问题。6‐9然而，这些方法通常需要进行大量全波分析，直到获得优化结构。其他方法通过使用计算成本低于全波技术的所谓代理模型进行优化步骤，从而提高算法的收敛速度。随后推导出特殊映射以关联精确空间模型。10‐14这些空间映射优化方法的主要缺点是需要两个模型（粗略与精细），并且当需要优化大量参数时，难以找到初始设计。此外，如果两个模型未充分对齐，则在粗略模型与精细模型之间找到非线性映射有时也很困难。

作为纯优化技术的一种替代方案，存在基于综合等效电路以满足最终期望指标的滤波器设计策略。然而，在传统滤波器设计技术中，滤波器结构中的各个耦合元件和谐振腔是分别进行尺寸设计的。因此，当所有元件组装成最终滤波器时，它们之间会出现相互作用和非期望耦合。这种效应在双模实现中更为显著，因为一个谐振腔容纳多个谐振模式。由于这些非期望效应，通常需要进行新的优化操作来校正整体响应。

对于这类滤波器，古列尔米和阿尔瓦雷斯‐梅尔孔提出了一种特别简单且有效的逐步设计方法21,22。该方法同样基于综合一个满足所需指标的初始等效电路。然而，后续的设计过程通过将电路分段，分多个步骤进行。通过这种方式，滤波器的设计从仅第一个谐振器开始，然后依次逐个添加其余谐振器，从而逐步得到完整的滤波器。采用这种方法，每一步仅涉及有限数量的参数。因此，可直接利用全波电磁仿真工具结合优化器非常高效地完成滤波器设计。该方法的另一个优点是，每一次优化步骤都考虑了相邻元件的存在及其相互作用。

古列尔米22所述的技术是为实现简单滤波功能的同向波导滤波器而开发的。然而，在许多应用中，需要具有例如传输零点或群延迟均衡等更复杂函数的功能。本文的目标和重要性在于，将古列尔米和阿尔瓦雷斯‐梅尔孔21,22提出的针对同向滤波器的设计技术，适配到耦合矩阵所确立的框架中。通过这种方式，我们首次开启了使用逐步分段技术来设计具有复杂耦合拓扑滤波器的可能性。

本文的结构如下。在第2节中，我们提出了一套完整的电路理论，可在耦合矩阵框架下应用逐步分段技术，以高效设计带通微波滤波器。该技术具有很强的通用性，可用于基于不同技术的滤波器设计。接着，在第3节中，我们给出了适用于矩形波导技术的具体方程，以实现所提出的技术。最后，在第4节中，通过设计一个复杂的六阶双模滤波器来演示该技术的应用，该滤波器在通带附近实现了3个传输零点。

该滤波器采用Guglielmi等人提出的双模全感性矩形波导技术实现24。此实例表明，所提出的设计技术在实现替代性和复杂耦合拓扑的波导滤波器尺寸设计方面非常有效。请注意，所介绍的设计技术也可用于具有其他耦合拓扑的滤波器设计，例如众所周知的四重结构25。然而，在本文中，我们选择了一个更为复杂的滤波器拓扑作为设计示例，以展示所提出设计技术即使在复杂场景下的性能表现。

基于耦合矩阵分割方法的设计过程的理论和精度通过实际制造的原型上设计的六阶滤波器的测量结果得到验证。

2 理论

为了应用逐步设计法，首先提取滤波器的等效电路。然后，该逐步设计法基于将等效电路及相应的滤波器结构分段，通过依次向初始结构中添加等效电路的不同元件（耦合元件和谐振器）来实现。21,22 将该设计技术应用于耦合矩阵背景下，需要对全局耦合矩阵进行分段，并从完整的矩阵中提取对应于滤波器各个独立部分的部分响应。通过从整体耦合矩阵中提取代表物理滤波器每一段的适当耦合元件和谐振器，实现耦合矩阵的分段。随后，可利用从等效电路各段获得的部分响应作为目标响应，以优化物理结构的每一部分。

将该技术应用于耦合矩阵形式，因此可以设计任何其拓扑可由以下广义耦合矩阵16,23表示的滤波器结构：

$$
M= \begin{bmatrix}
0 & M_{S1} & M_{S2} & \cdots & M_{SN} & M_{SL} \
M_{1S} & M_{11} & M_{12} & \cdots & M_{1N} & M_{1L} \
M_{2S} & M_{21} & M_{22} & \cdots & M_{2N} & M_{2L} \
\vdots & \vdots & \vdots & \ddots & \vdots & \vdots \
M_{NS} & M_{N1} & M_{N2} & \cdots & M_{NN} & M_{NL} \
M_{LS} & M_{L1} & M_{L2} & \cdots & M_{LN} & 0 \
\end{bmatrix}. \tag{1}
$$

在此矩阵中，元素 $M_{Si}= M_{iS}$ 表示从源到第 $i$ 个谐振器的输入耦合，元素 $M_{ij}(i≠j)$ 对应第 $i$ 个和第 $j$ 个谐振器之间的耦合，而 $M_{jL}= M_{Lj}$ 元素表示从第 $j$ 个谐振器到负载的输出耦合。最后，主对角线上的元素（$M_{ii}$）与频率不变电抗（FIR）元件相关。这些元件用于引入每个谐振器谐振频率相对于滤波器中心频率的频率偏移，在异步调谐拓扑中需要这些元件。

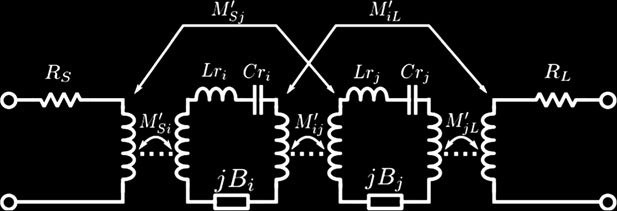
方程1中的广义耦合矩阵表征了图1A所示的低通网络，当所有电路元件均以如下形式归一化时：

$$
R_S= R_L= L_i= 1, B_i= M_{ii}, \tag{2}
$$

其中，$R_S$和$R_L$为滤波器的端接阻抗，$B_i$为FIR元件的值。因此，该归一化耦合矩阵给出了给定滤波器的总响应，其中源和负载阻抗已被缩放至单位值。然而，在应用逐步分割过程时，需要获得与滤波器结构特定部分相关的部分响应。可以证明，这些部分响应无法直接从归一化耦合矩阵中提取，因为内部耦合元件不能像外部耦合那样直接转换。因此，必须进行耦合矩阵缩放，以便能够对全局耦合矩阵进行分段，并获得正确的小部分响应。

缩放后的耦合矩阵仍将对应于图1A所示的低通原型。然而，低通电路中的电感器（$L_i$）、FIR元件（$B_i$）以及负载阻抗（$R_S,R_L$）将利用图1B所示带通原型中实际谐振器所提供的信息进行缩放，该带通原型是通过经典低通到带通变换获得的。26该缩放过程通过使用将在特定技术中实现的物理滤波器的实际谐振器所提供的信息来完成。在此缩放完成后，得到一个新的矩阵（$M’$），该矩阵可有效用于获取给定滤波器所需的部分响应。

当图1A所示低通原型中的电路元件与单位值不同时，耦合矩阵的缩放以常规方式进行。26对于输入和输出元件，我们得到

$$
M’ {Si}^2= R_S L_i M {Si}^2, \quad M’ {iL}^2= R_L L_i M {iL}^2. \tag{3}
$$

对于滤波网络内的所有其他逆变器，我们有

$$
M’ {ij}^2= L_i L_j M {ij}^2. \tag{4}
$$

上述关系对于谐振器间耦合（$i ≠j$）和自元件（$i=j$）均成立，其中自元件考虑了滤波器谐振器谐振频率的偏移为。了完成缩放任务，进而计算矩阵（$M’$），必须获得$R_S$、$R_L$和$L_i$的正确值。这些参数必须从物理结构中获取，并考虑所需带通滤波器将要实现的技术。

使用经典低通到带通变换，图1A所示的低通原型转换为图1B所示的带通电路。26通过该过程，低通网络中的每个电路元件（$L_i$）在带通域中被转换为具有斜率参数（$X_i$）的谐振器$L_{ri}C_{ri}$。两者之间的关系可表示为26

$$
L_i= \frac{FB}{\omega’ 1} X_i= \frac{FB}{\omega’_1} \frac{\omega_0}{L {ri}}, \tag{5}
$$

其中$\omega_0$表示带通滤波器的中心角频率，$FB= \frac{\omega_2-\omega_1}{\omega_0}$ 为分数带宽，$\omega_1’$为低通原型的归一化截止频率（通常取单位值），而($L_{ri}$)为带通原型中谐振器的集总电感。

带通原型中串联LC谐振器的电容值是通过以下方式获得的：

$$
C_{ri}= \frac{1}{L_{ri}\omega_0^2}. \tag{6}
$$

以类似的方式，FIR元件（$B_i$）可以重新定义为以下形式：

$$
B_i= -\frac{B_{ri}}{FB f_0} = -\frac{B_{ri}}{FB \omega_0 / 2\pi}. \tag{7}
$$

由于原始电路元件表示图1A所示的低通网络，因此无法从遵循图1B所示带通网络的最终滤波器结构直接计算得到。因此，首先从实际滤波器结构中获取图1B中带通原型的集总元件值，然后通过逆序应用低通到带通变换，得到图1A中的低通原型元件。

3 APPLICATION TO RECTANGULAR WAVEGUIDE TECHNOLOGY

接下来，我们将说明如何将前一节介绍的理论应用于采用矩形波导技术实现的带通滤波器。类似的方法也可应用于基于其他技术（如广泛使用的微带技术）的微波带通滤波器的设计。

首先，需要考虑波导技术中的合适谐振器以及正确的谐振模式（$TE_{mnp}$）或（$TM_{mnp}$）。该谐振器可以用图2所示的经典传输线等效电路（串联或并联）进行建模。

以串联等效电路为例，关键思想是建立物理波导滤波器中的实际谐振器与通用集总元件谐振器之间的等效关系，如图2所示。注意，谐振器的输入阻抗在谐振频率处恰好为零。为了使图2中所示的集总元件谐振器与传输线谐振器等效，将在接近谐振频率的另一频率处使两个谐振器的输入阻抗相等。这相当于强制传输线谐振器具有与集总（ LC）谐振器相似的斜率参数。为此，我们选择使用滤波器的上截止频率（$\omega_2$），对于窄带滤波器而言，该频率始终接近单个谐振器的谐振频率（$\omega_{ri}$）。

接下来，我们首先考虑传输线谐振器在滤波器上截止频率处的输入阻抗（$\omega_2$）

$$
Z_{IN,i} = j \frac{\omega_2 \mu}{\beta_{2,mn}} \tan\left(\beta_{2,mn} \frac{\lambda_{g,ri}}{2p}\right), \tag{8}
$$

其中我们使用了在第 $k$ 个频率 $(\beta_{kmn})$ 处相应模式的传播常数的定义

$$
\beta_{kmn}= \sqrt{(\omega_k \sqrt{\varepsilon\mu})^2 -\left(\frac{m\pi}{a}\right)^2 -\left(\frac{n\pi}{b}\right)^2}; \tag{9}
$$

在该方程中，$a$ 和 $b$ 分别是波导的宽度和高度。注意，导波波长 $(\lambda_{g,ri})$ 并非在滤波器的中心频率处计算，而是在谐振器的实际谐振频率 $(\omega_{ri})$ 处计算。因此，其计算方式如下

$$
\beta_{ri,mn}= \sqrt{(\omega_{ri} \sqrt{\varepsilon\mu})^2 -\left(\frac{m\pi}{a}\right)^2 -\left(\frac{n\pi}{b}\right)^2}, \quad \lambda_{g,ri}= \frac{2\pi}{\beta_{ri,mn}}. \tag{10}
$$

下一步是将波导谐振器在滤波器上截止频率处计算得到的输入阻抗与通用集总元件串联谐振器的输入阻抗相等。我们首先写出通用集总元件串联谐振器的输入阻抗表达式

$$
Z_{IN,eq,i} = j \frac{1}{\omega_{ri} C_{ri}}\left( \frac{\omega_2}{\omega_{ri}} - \frac{\omega_{ri}}{\omega_2} \right) = j\omega_{ri}L_{ri}\left( \frac{\omega_2}{\omega_{ri}} - \frac{\omega_{ri}}{\omega_2} \right). \tag{11}
$$

请注意，在前面的表达式中，再次强调，未使用滤波器的中心频率（$\omega_0$）。相反，重要的是使用谐振器的实际谐振角频率（$\omega_{ri}$）。

通用谐振器的实际谐振角频率可以从公式7所示的FIR元件中获取

$$
\omega_{ri}= \pi\left(B_{ri}+ \sqrt{B_{ri}^2+\left(\frac{\omega_0}{\pi}\right)^2}\right). \tag{12}
$$

将(11)与(8)结合，可得到集总元件谐振器的电感（$L_{ri}$）的表达式：

$$
L_{ri}= \frac{\omega_2 \mu}{\beta_{2,mn}} \tan\left(\beta_{2,mn} \frac{\lambda_{g,ri}}{2p}\right)\left[\omega_{ri}\left( \frac{\omega_2}{\omega_{ri}} - \frac{\omega_{ri}}{\omega_2} \right)\right]^{-1}. \tag{13}
$$

需要强调的是，这种等效性是在滤波器的上截止频率处强制实现的。这是因为在该频率下，谐振器表现出轻微的电感性行为，且电感（$L_{ri}$）占主导地位。当然，也可以通过在低通原型中使用并联电容以及在带通原型中使用并联谐振器来推导出对偶表达式。在这种情况下，过程类似，但更方便在下截止频率处强制实现两种谐振器模型之间的等效性，因为此时电容性行为占主导地位。

一旦获得集总谐振器的电感（$L_{ri}$），即可利用公式5计算图1A中低通原型电感器的缩放值。此外，源（$R_S$）和负载（$R_L$）阻抗也被缩放至用作接入端口的终端波导中主模的特性阻抗。在矩形波导中，这通常是模式（$TE_{10}$）：

$$
R_S= R_L= Z^{TE_{10}} 0 = \frac{\omega_k \mu}{\beta {k,10}}. \tag{14}
$$

注意，通过此步骤，耦合矩阵的所有元素都可以根据公式3和4进行缩放，从而得到完整的已缩放的（$M’$）矩阵。

4 示例说明

本文推导的理论的主要优势在于，首次在古列尔米和阿尔瓦雷斯‐梅尔孔21,22中提出的逐步分段设计技术可用于有效设计实现复杂耦合拓扑的实用滤波器16，而不仅限于较简单的级联结构。

为了展示所提出理论的有效性，本节包含了一个基于双模谐振腔的六阶复杂滤波器的设计，该设计遵循 Guglielmi等人提出的全感性波导技术24。通常情况下，由于需要优化的参数数量较多，并且响应对耦合和谐振器具有高度敏感性，双模滤波器的设计相当复杂。这种复杂性还源于一个物理谐振腔控制多个共振频率的事实。尽管存在这些困难，我们将证明本文推导出的设计方法非常有效，能够快速确定满足初始目标指标的整个波导结构的尺寸。

具有传输零点的其他较简单耦合拓扑，例如四重拓扑25，也可以使用本文提出的技术进行设计。然而，我们希望在论文中说明所推导的技术确实功能强大，可用于包含多个交叉耦合的复杂耦合拓扑滤波器的实际设计，如图4所示。

在我们的示例中，该结构由3个双模谐振腔组成，如图3所示，实现了图4所示的耦合拓扑。在图4中，通过虚线框标出了物理结构中的谐振腔与等效电路中的谐振器之间的对应关系。

需要注意的是，Cameron 等人27已证明图4中的耦合拓扑与图3中采用全感性波导技术的物理实现之间具有等效性。然而，目前尚无简单的设计流程可用于从初始指标出发，系统地对波导结构的各个部分进行尺寸设计。

设计示例所需的电气特性为中心频率（$f_0= 3.9$吉赫）、带宽（$BW=100$兆赫）和回波损耗（$RL= 15$分贝）。将在有限频率处实现三个传输零点，分别为（$f_{z1}= 3.825$吉赫、$f_{z2}= 3.958$吉赫和$f_{z3}=3.970$吉赫）。输入和输出端口采用标准 WR‐229 波导（58.17 × 29.083毫米）实现。根据 Martinez‐Mendoza 等人所述的综合技术，得到归一化耦合矩阵为

$$
M= \begin{bmatrix}
0 & -0.756 & -0.462 & 0 & 0 & 0 & 0 & 0 \
-0.756 & -0.365 & 0 & 0.512 & 0.306 & 0 & 0 & 0 \
-0.462 & 0 & 1.017 & -0.147 & -0.088 & 0 & 0 & 0 \
0 & 0.512 & -0.147 & 0.294 & 0 & -0.066 & 0.569 & 0 \
0 & 0.306 & -0.088 & 0 & -0.811 & 0.033 & -0.288 & 0 \
0 & 0 & 0 & -0.066 & 0.033 & -1.034 & 0 & 0.389 \
0 & 0 & 0 & 0.569 & -0.288 & 0 & 0.262 & 0.795 \
0 & 0 & 0 & 0 & 0 & 0.389 & 0.795 & 0 \
\end{bmatrix}. \tag{15}
$$

通过遵循上一节中描述的步骤，归一化耦合矩阵将被缩放，以获得逐步设计法中所需的（$M’$）矩阵。首先，必须根据公式13计算带通滤波器原型的电感。在该公式中，需要使用每个双模谐振腔中两个谐振模式对应的传播常数（公式(9)）。因此，需要预先计算双模腔体的初始尺寸。

为了计算孤立矩形谐振腔的初始尺寸，我们首先使用具有尺寸（$A_q,B_q,L_q$）的矩形腔谐振器的谐振频率公式

$$
\omega_{ri}= \pi \sqrt{\varepsilon\mu}\sqrt{\left(\frac{m_i}{A_q}\right)^2 +\left(\frac{n_i}{B_q}\right)^2 +\left(\frac{p_i}{L_q}\right)^2}, \tag{16}
$$

其中$m_i$、$n_i$和$p_i$为谐振腔内某一通用谐振模式（i）的索引。根据该方程，可计算出产生给定谐振角频率（$\omega_{ri}$）所需的第$q$个谐振腔的尺寸。求解$A_q$、$B_q$和$L_q$，可得

$$
A_q^2= \frac{m_i^2}{\varepsilon\mu\left( \frac{\omega_{ri}}{\pi} \right)^2 -\left(\frac{n_i}{B_q}\right)^2 -\left(\frac{p_i}{L_q}\right)^2}, \tag{17}
$$

$$
B_q^2= \frac{n_i^2}{\varepsilon\mu\left( \frac{\omega_{ri}}{\pi} \right)^2 -\left(\frac{m_i}{A_q}\right)^2 -\left(\frac{p_i}{L_q}\right)^2}, \tag{18}
$$

$$
L_q^2= \frac{p_i^2}{\varepsilon\mu\left( \frac{\omega_{ri}}{\pi} \right)^2 -\left(\frac{m_i}{A_q}\right)^2 -\left(\frac{n_i}{B_q}\right)^2}. \tag{19}
$$

利用这些方程，我们现在可以计算孤立的第$q$个谐振腔（$q= 1,2, 3$）的尺寸，使其同时支持两个谐振（ $\omega_{ri}$和 $\omega_{rj}$），这两个谐振由耦合矩阵的对角元素通过公式12给出。每个谐振腔中用于构建滤波器的两个模式是$TE_{m_i,0,p_i}$和$TE_{m_j,0,p_j}$。因此，可通过在两个谐振频率处令公式17和19相等，然后求解（$A_q$）和（$L_q$）得到谐振腔的尺寸。这一简单过程可得出

$$
A_q^2 = \frac{\pi^2}{\varepsilon\mu} \frac{(m_i p_j)^2 -(m_j p_i)^2}{(p_j \omega_{ri})^2 -(p_i \omega_{rj})^2}, \tag{20}
$$

$$
L_q^2 = \frac{\pi^2}{\varepsilon\mu} \frac{(p_j m_i)^2 -(p_i m_j)^2}{(m_i \omega_{rj})^2 -(m_j \omega_{ri})^2}. \tag{21}
$$

请注意，此过程中不需要方程18，因为每个谐振腔中使用的两个谐振模式具有$n_i= n_j= 0$。最后这两个方程特别有用，因为通过已知模式的模态指数以及第$q$个谐振腔所支持的两个相关角谐振频率（$\omega_{ri}$和$\omega_{rj}$），我们可以很容易地获得相应谐振腔的初始物理尺寸。

在应用缩放过程之前，需要解决的最后一个问题是如何将每个双模腔体中的正确谐振模式映射到图4所示耦合拓扑中对应的谐振器。这个问题可以通过注意到归一化耦合值到模式$TE_{102}$始终大于到模式$TE_{201}$的耦合值来轻松解决。例如，如果我们关注耦合矩阵的第一列，会发现$M_{S1}> M_{S2}$。因此，在第一个双模腔体中，正确的谐振模式映射应将模式$TE_{102}$对应于图4中的谐振器1，而模式$TE_{201}$对应于谐振器2。其余双模腔体也需遵循相同的规则，从而得到表1所示的映射关系。

一旦确定了每个谐振腔中的正确模式，就可以使用方程20和21计算初始尺寸。我们将通过详细说明滤波器示例中第一个腔体的步骤来展示该过程。根据表1，该腔体中两个模式的模态指数为（$m_i= 1$, $n_i= 0$, $p_i= 2$）和（$m_j= 2$, $n_j= 0$, $p_j= 1$）。接下来，我们需要使用方程7和12计算第一个腔体支持的两个谐振频率。前两个谐振器的 FIR元件取自耦合矩阵对角线上的前两个非零元素，即$B_i= -0.365,B_j= 1.017$。根据这些数据，得到两个角谐振频率为$\omega_{ri}= 24.62 \cdot 10^9$(rad/seg)（$f_{ri}= 3.92$吉赫）和$\omega_{rj}= 24.19 \cdot 10^9$(rad/seg)（$f_{rj}= 3.85$吉赫）。结合模态指数以及该第一个腔体所支持的两个谐振频率，现在可通过方程20和21计算出尺寸，得到$A= 87.7$毫米和$L= 85.1$毫米。

根据这些步骤，该滤波器示例的3个双模谐振腔的初始尺寸如表2所示。需要强调的是，表2中给出的独立腔体的初始尺寸用于两个主要目的：首先，它们用于计算不同波导段中各模式的传播常数，这是公式13所需要的；其次，它们作为接下来将详细介绍的结构各段优化的初始点。

表1 每个双模谐振腔中各谐振器与各谐振模式的对应关系
谐振器
1
2
3
4
5
6

| 表2 作为示例的六阶滤波器中双模谐振腔的初始尺寸，具有3个传输零点 |
|—|
| | 第一个腔体 | 第二型腔 | 第三型腔 |
| | A2(毫米) | L2(毫米) | A4(毫米) | L4(毫米) | A6(毫米) | L6(毫米) |
| | 87.7 | 85.1 | 84.7 | 86.7 | 84.4 | 86.8 |
一旦已知谐振腔的初始尺寸，现在就可以通过公式13计算带通电路原型中电感器的值。接下来，使用公式5计算低通原型中的电感器值。最后，利用公式3和4计算缩放后的耦合矩阵的各个元素。我们将通过计算缩放后的$M_{S1}’$和$M_{11}’$元素来说明该过程。第一个元素表示从源到第一个腔体第一模式的耦合。根据表1，这对应于模态指数 ($m= 1$, $n= 0,p= 2$)。利用此前计算得到的该腔体的初始尺寸（$A= 87.6$ mm），我们可以根据上截止频率 $(\beta_{2,mn})$以及谐振器的谐振频率$(\omega_{ri}= 24.62 \cdot 10^9$(rad/seg)，$f_{ri}= 3.92$吉赫)使用公式9和10计算传播常数$(\beta_{ri,mn})$，得到 $\beta_{2,mn}= 74.63$(弧度/米)和 $\beta_{ri,mn}= 73.90$(弧度/米)。于是，谐振频率下的导波波长变为 $\lambda_{g,ri}= 85$毫米。

根据这些信息，我们现在可以使用公式13计算带通域中谐振器电感的值，得到$L_{ri}= 66.16$nH。低通原型中电感的值通过公式5计算得出，

表3 基于图5所示集总元件等效电路的谐振器值($Z_{port1}= Z_{port2}= 501.89\Omega$)
谐振器1
谐振器2
谐振器3
谐振器4
谐振器5
谐振器6

为$L_i= 41.56$H。方程3表明，要缩放元件$M_{S1}$，需要源阻抗。在我们的滤波器结构中，这是指由波导标准 WR‐229（$a= 58.17$ mm，$b= 29.083$mm）构成的输入端口内基本模式 $TE_{10}$ 的特性阻抗。该阻抗可通过方程14 在滤波器的中心频率（$\omega_0$）处简单计算得到，结果为$R_S= 501.89\Omega$。随后可使用公式3和4计算缩放后的耦合矩阵的相应元素，最终得到$M_{S1}’= -109.18$，$M_{11}’= -15.16$。

可以对第一个腔体支持的第二谐振模式采用类似的过程。在这种情况下，根据表1，该谐振模式的模态指数为 $(m= 2,n= 0$, $p= 1)$。此模式将涉及矩阵中表示从源到第二个谐振器的耦合的元素$(M_{S2}= -0.462)$，以及第二个谐振器的谐振频率$(M_{22}= B_2= 1.017)$，$(\omega_{rj}= 24.19 \cdot 10^9$(弧度/秒)，$f_{rj}= 3.85$吉赫)。重复相同的计算可得到 $\beta_{2,mn}= 41.48$(弧度/米)， $\beta_{rj,mn}= 37.1$(弧度/米)，和 $\lambda_{g,rj}= 169.4$毫米。第二个谐振器的电感变为$L_{rj}= 235.79$纳亨，低通原型中的电感为$L_j= 148.15$亨。最终的缩放值则为$M_{S2}’= -125.68$，$M_{22}’= 150.10$。

通过对滤波器结构的所有谐振腔重复相同的过程，最终得到缩放后的耦合矩阵（$M’$）

$$
M’= \begin{bmatrix}
0 & -109.18 & -125.68 & 0 & 0 & 0 & 0 & 0 \
-109.18 & -15.16 & 0 & 21.79 & 26.07 & 0 & 0 & 0 \
-125.68 & 0 & 150.10 & -11.78 & -14.09 & 0 & 0 & 0 \
0 & 21.79 & -11.78 & 12.79 & 0 & -5.80 & 24.81 & 0 \
0 & 26.07 & -14.09 & 0 & -141.65 & 5.87 & -25.09 & 0 \
0 & 0 & 0 & -5.81 & 5.87 & -184.49 & 0 & 116.60 \
0 & 0 & 0 & 24.81 & -25.09 & 0 & 11.41 & 117.65 \
0 & 0 & 0 & 0 & 0 & 116.60 & 117.65 & 0 \
\end{bmatrix}. \tag{22}
$$

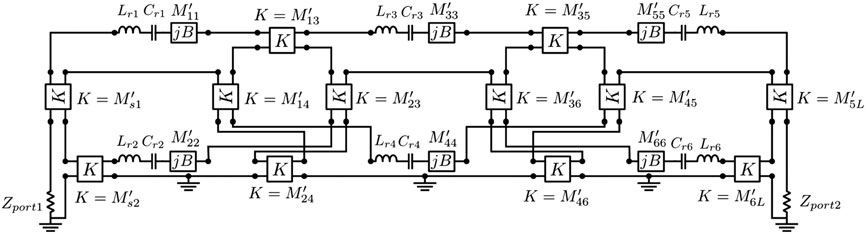
基于图1所示通用电路，该滤波器拓扑对应的集总元件等效电路如图5所示。在此电路中，变压器和交叉耦合通过理想阻抗倒相器实现。该电路中各元件的值列于表3中。其中，FIR元件（$B$）的值为缩放后矩阵（22）对角元素 （$M’ {ii}$），而阻抗逆变器（$K$）的值为矩阵的非对角元素（$M’ {ij}$），如图5所示。该电路的响应满足初始指标，这将在设计过程结束时予以验证。

一旦耦合矩阵被缩放，逐步设计方法便可开始。缩放后的耦合矩阵的第一段是

$$
M’ 1(\text{Mode } TE {10}) =\begin{bmatrix} 0 & -109.18 \ -109.18 & 0\end{bmatrix}, \tag{23}
$$

$$
M’ 1(\text{Mode } TE {20}) =\begin{bmatrix} 0 & -125.68 \ -125.68 & 0\end{bmatrix}. \tag{24}
$$

注意，该段包含两个子矩阵。这是为了从输入端口提取到前两个谐振器的耦合（第一个子矩阵对应$M_{S1}$，第二个子矩阵对应$M_{S2}$）。此外，在构建该段时，全局矩阵（22）中的元素（$M_{11}$和$M_{22}$）在相应的子矩阵中被设为零。这是必要的，因为第一个谐振器变为非谐振节点，充当中间输出端口。

该段对应的物理波导结构如图6所示。从图6可以看出，该段中的输出波导（参数$A_2$）已设置为先前为第一个谐振腔获得的初始宽度（如表2所示为87.7毫米）。此外，孔径宽度（$A_1$）也被固定。原因是这类双模腔体需要具有相等宽度的输入和输出孔径（$A_1$ 和 $A_3$），以保持腔体内两种模式的场分布正交。如果两个孔径的宽度存在显著差异（$A_1 \ne A_3$），则无法利用现有的几何参数独立调节两个谐振频率。因此，在设计中，所有孔径宽度（$A_1, A_3, A_5,$ 和$A_7$）都将固定为一个给定值。在此情况下，每个双模腔体中对两个谐振模式的耦合量将仅通过调节孔径的厚度和偏移来实现。在本示例中，我们选择了$A_1=A_3=A_5=A_7= 27$毫米，因为该值可使所有孔径的最小厚度保持在约2毫米左右（有利于制造工艺）。

连接两个输入/输出波导的窗口充当渐逝波导段。因此，通过其厚度($L_1$)可以调节到$TE_{10}$和$TE_{20}$的耦合（见图6）。此外，由于对称性，使用居中窗口时不会激励模式$TE_{20}$。因此，该模式的激励主要依赖于引入一个偏移量($T_1$)，如图6所示。

因此，第一段的优化包括调节第一个孔径的厚度（$L_1$）和偏移量（$T_1$）（见图6），以获得由公式23和24中的子矩阵给出的与模式$TE_{10}$和$TE_{20}$所需的耦合。本文中，使用FEST3D29,30对所有波导结构进行全波分析，并且其基于梯度技术的优化引擎被用于所有的优化操作。

第一个优化任务非常简单，因为它仅涉及两个参数（$L_1$ 和 $T_1$）。结果如图7所示。水平线表示耦合矩阵(23)和(24)预测的到作为输出端口的波导中模式$TE_{10}$和$TE_{20}$的耦合水平。红色（圆圈）和蓝色（菱形）线条表示图6所示波导结构的全波响应。可以观察到，在滤波器的中心频率处，对这两个模式的耦合水平均被准确复现。该优化阶段后获得的相关尺寸汇总于表4中。

第一段优化完成后，第二步是将下一段添加到结构中，如图8所示。可以看出，第二段是通过在前一阶段增加一个额外的耦合孔和谐振腔而得到的。注意，此时第二型腔在此第二段中充当输出端口。为了定义输出端口，第二个谐振腔的宽度（$A_4$）被固定为表2中给出的初始值（$A_4= 84.7$毫米）。此外，在此阶段，第一个谐振腔的长度（$L_2$）仍未知。在开始优化过程之前，该长度将被固定为表2中给出的初始值（$L_2= 85.1$毫米）。

现在可以从公式22中的缩放后的耦合矩阵提取该第二段的响应。同样，必须考虑2个子矩阵，以计入图8中间输出波导中与$TE_{10}$和$TE_{20}$模式的耦合，从而得到

$$
M’ 2(\text{Mode } TE {10})= \begin{bmatrix}
0 & -109.18 & -125.68 & 0 \
-109.18 & -15.16 & 0 & 21.79 \
-125.68 & 0 & 150.10 & -11.78 \
0 & 21.79 & -11.78 & 0 \
\end{bmatrix}, \tag{25}
$$

$$
M’ 2(\text{Mode } TE {20})= \begin{bmatrix}
0 & -109.18 & -125.68 & 0 \
-109.18 & -15.16 & 0 & 26.07 \
-125.68 & 0 & 150.10 & -14.09 \
0 & 26.07 & -14.09 & 0 \
\end{bmatrix}. \tag{26}
$$

请注意，子矩阵对角线的最后一个元素必须设为零。这是因为在最终结构中，第二段的第二个谐振器充当输出端口。为了便于说明，我们在图9中给出了代表该设计流程第二段中对应这两个子矩阵的耦合拓扑的子电路。可以看出，这些拓扑包含了第一型腔的前两个谐振器。第二型腔的第一模式作为第一个子电路（式(25)中的耦合矩阵）的输出端口，而第二模式则作为第二个子电路（式(26)中的耦合矩阵）的输出端口。

这两个子矩阵的响应现在被用作图8所示波导结构优化的目标响应。

表4 图6所示第1段获得的初始和优化尺寸
参数
$L_1$
$T_1$

该段的优化由两个步骤组成。在第一步中，仅调整与新段相关的参数，即第一个谐振腔的长度（$L_2$）、第二个耦合孔的厚度（$L_3$）以及与该第二个耦合孔相关的偏移（$T_2$和$T_3$）。该优化过程涉及4个参数，可获得接近优化值的几何尺寸，这些尺寸将作为第二步的起始点。在第二步中，将对结构的所有相关参数进行重新优化（$A_1, L_1, L_2, L_3, T_1, T_2,$和$T_3$），以精确匹配由表示该第二段的两个子矩阵给出的目标响应的形状（见公式25和(26)）。

该优化过程的结果如图10所示。我们可以观察到两个子矩阵的响应，以及图8所示结构的全波响应。可以看出，该优化过程是非常有效的，且目标响应的形状和水平都得到了非常精确的还原。设计过程中此阶段提取的结构相关尺寸汇总于表5。

目前优化的两段对应滤波器的前半部分。然而，由于该滤波器不对称，必须从滤波器末端开始，对后半部分重复相同的步骤，并考虑表1中所示的模式与谐振器之间的映射关系。具体操作方法与前述滤波器前半部分的处理方式完全相同，因此不再赘述。滤波器后半部分最终优化得到的尺寸列于表6中。

在对滤波器的前半部分和后半部分的前两段完成尺寸设计后，唯一未知的参数是中心腔的宽度和长度（如图3所示的$L_4$和$A_4$）。为了计算这些参数，例如可在滤波器的前半部分增加第三段，如图11所示。构建该段时，最后一个谐振腔的几何参数（$L_5,A_6, T_4, T_5$）取自上一步后半段优化过程中计算得到的值。对于中心腔的初始尺寸（$L_4, A_4$），即唯一剩余的未知参数，其初始值来自表2中计算的结果。从公式22的全局缩放矩阵中提取出的、表示图11结构的两个子矩阵为

$$
M’ 3(\text{Mode } TE {10})= \begin{bmatrix}
0 & -109.18 & -125.68 & 0 & 0 & 0 \
-109.18 & -15.16 & 0 & 21.79 & 26.07 & 0 \
-125.68 & 0 & 150.10 & -11.78 & -14.09 & 0 \
0 & 21.79 & -11.78 & 12.79 & 0 & 24.81 \
0 & 26.07 & -14.09 & 0 & -141.65 & -25.09 \
0 & 0 & 0 & 24.81 & -25.09 & 0 \
\end{bmatrix}, \tag{27}
$$

$$
M’ 3(\text{Mode } TE {20})= \begin{bmatrix}
0 & -109.18 & -125.68 & 0 & 0 & 0 \
-109.18 & -15.16 & 0 & 21.79 & 26.07 & 0 \
-125.68 & 0 & 150.10 & -11.78 & -14.09 & 0 \
0 & 21.79 & -11.78 & 12.79 & 0 & -5.81 \
0 & 26.07 & -14.09 & 0 & -141.65 & 5.87 \
0 & 0 & 0 & -5.81 & 5.87 & 0 \
\end{bmatrix}. \tag{28}
$$

此时需要强调的是，在最后这一优化步骤中，只需调整参数$L_4$和$A_4$，因为它们与滤波器结构其余部分的相互作用极小。这使得在最后阶段的优化过程非常简单。最终优化后的参数汇总于表7。

表5 第二段获得的初始和优化尺寸
参数
$L_1$
$T_1$
$L_2$
$A_2$
$T_2$
$L_3$
$T_3$

表6 滤波器后半部分获得的初始和优化尺寸
参数
$L_7$
$T_6$
$L_6$
$A_6$
$T_5$
$L_5$
$T_4$

表7 中心腔获得的初始和优化尺寸
参数
$L_4$
$A_4$

经过最后一步后，从期望的耦合矩阵出发，应用设计技术得到的初始尺寸汇总于表4‐6和表7。

在使用所述的逐步设计法获得滤波器的所有尺寸后，将整个滤波器组装起来，结果如图12A所示。在图中，给出了从耦合矩阵（公式(15)）或图5所示的等效电路获得的理想响应，展示了滤波器的预期行为。

使用FEST3D对波导结构在组装后的全波仿真结果也已给出，用于对比。可以看出，设计的滤波器与目标响应非常接近。事实上，三个传输零点均位于精确位置，且带宽已完美恢复。此外，响应中显示了所有反射零点，尽管回波损耗是滤波器响应中最敏感的参数。由于设计结果已非常接近目标响应，因此可以很容易地进行最终全局优化，而无需担心陷入局部最小值。FEST3D29中实现的简单基于梯度的方法提供了最终优化后的滤波器，其响应如图 12B所示。该最终全局优化步骤后的结构最终尺寸列于表8中。

该滤波器已制造并测试，以验证新提出的设计技术的实际可行性。为了对设计的滤波器进行实验验证，选用了带有10个孔（UDR‐40）的矩形标准平焊法兰用于输入/输出矩形波导（WR‐229）。该滤波器由铝制成，通过精度优于 20 μm的计算机控制铣削工艺加工完成，加工由航空航天公司Forestal执行。在图13中，我们给出了用于测试原型的测量系统，该系统包括一个矢量网络分析仪以及先前的直通、反射、负载（TRL）校准。

表8 最终全局优化后得到的滤波器尺寸
参数
$A_1$
$A_2$
$A_3$
$A_4$
$A_5$
$A_6$
$A_7$
参数
$T_1$
$T_2$
$T_3$

图14显示了FEST3D仿真结果与实际硬件测量结果的对比。仿真与测量结果之间表现出极好的一致性。可以看出，实测滤波器的通带内和带外性能非常接近目标指标，即$f_0= 3.893$吉赫，$BW= 104.8$兆赫，$f_{z1}= 3.834$吉赫， $f_{z2}= 3.957$吉赫，以及 $f_{z3}= 3.965$吉赫。测得的插入损耗在中心频率处为0.32 dB，通带内的回波损耗低于14.3 dB。

5 结论

本文提出了一种高效设计实现复杂耦合拓扑的波导滤波器的新策略。该方法基于一种分段技术，通过优化多个简单阶段来完成整个结构的设计。本文的主要贡献是将该技术适配到耦合矩阵形式的框架中。因此，本文首次实现了将此设计技术用于具有复杂耦合拓扑的滤波器。该策略通过设计一个采用全感性双模谐振腔实现的复杂六阶带通滤波器进行了验证，该滤波器在通带附近具有3个传输零点。全波仿真结果表明，所提出的策略对该结构的设计确实非常有效。此外，理论结果和全波仿真结果已通过实际制造的原型的测量结果成功验证。只要相关复杂耦合拓扑能够用经典的耦合矩阵方法表示，所提出的这项技术预计将在这些滤波器的设计中具有广泛应用价值。