NOIP2023模拟2联测23 分神

矩形移动操作的二维前缀和查询解决方案,

最新推荐文章于 2025-12-12 16:37:00 发布

原创最新推荐文章于 2025-12-12 16:37:00 发布 · 453 阅读

0 ·

CC 4.0 BY-SA版权

文章标签：

#题解 #c++

题解同时被 2 个专栏收录

348 篇文章

订阅专栏

好题

52 篇文章

订阅专栏

文章描述了一个涉及矩形移动和查询的问题，利用差分和线段树技术实现高效的二维前缀和计算，以解决包含特定点的矩形数量问题。

题目大意

有 $n$ 个矩形，每个矩形的四条边都平行于坐标轴。对于一个矩形，它的左下角坐标为 $x_1,y_1)$ ，右上角坐标为 $x_2,y_2)$ ，包含了所有满足 $x1≤x≤x2,y1≤y≤y2x_1\leq x\leq x_2,y_1\leq y\leq y_2$ 的点 $(x, y)$ 。

接下来要对这些矩形进行 $m$ 次移动操作。每次移动会选择一个矩形，具体的移动可以用方向和距离表示。方向分别为，上、下、左、右、左上、左下、右上、右下，方向向量分别为 $(1, 0), (1, 1), (0, 1), (- 1, 1), (- 1, 0), (- 1, - 1), (0, - 1), (1, - 1)$ ，距离为一个正整数 $d$ 。

假设矩形的左下角的坐标为 $(a, b)$ ，方向向量为 $(d x, d y)$ ，那么矩形的左下角会移动到位置 $(a+d×dx,b+d×dy)(a+d\times dx,b+d\times dy)$ ，右上角也同理。同时，这个矩形在移动的过程中，会把中间过程都保留下来。也就是说，矩形移动到位置 $(a+d×dx,b+d×dy)(a+d\times dx,b+d\times dy)$ ，会产生 $d$ 个新的矩形，左下角为 $(a+i×dx,b+i×dy)(a+i\times dx,b+i\times dy)$ ，其中 $0≤i≤d−10\leq i\leq d-1$ ，大小和原矩形相同。

$m$ 次操作之后，有 $q$ 次询问，每次给你一个点 $(p x, p y)$ ，问有多少个矩形包含这个点。

$0≤n,m,q≤2500000\leq n,m,q\leq 250000$ ，所有坐标范围在 $1$ 到 $250000$ 之间。

这里的坐标范围指矩形在所有时间的坐标都在这个范围内，并且查询的点也在这个范围内。

时间限制 $3000 m s$ ，空间限制 $512 MB$ 。

题解

考虑差分，对于一个矩形，我们可以将其差分成坐标系上的四个带权的点，那么矩形的移动就可以差分成若干条带权的边。于是，每次查询就是求差分后的图的二维前缀和。

对于方向相反的操作我们可以看作同一种，也就是说，线段只会有横着、竖着、左斜和右斜两种。

对于横着的线段，我们竖着跑扫描线，边修改边查询，注意同一位置的修改应在查询前面。

对于竖着的线段，我们可以将坐标轴翻转，然后就可以按处理横着的线段的方法来处理了。

对于左斜的线段，我们发现每条线段上的点的 $x + y$ 是相同的，于是我们可以右斜着跑扫描线。对于每次修改，我们在 $x$ 方向和 $y$ 方向上都做修改。对于每次查询，设查询的点为 $(x, y)$ ，我们观察图像。

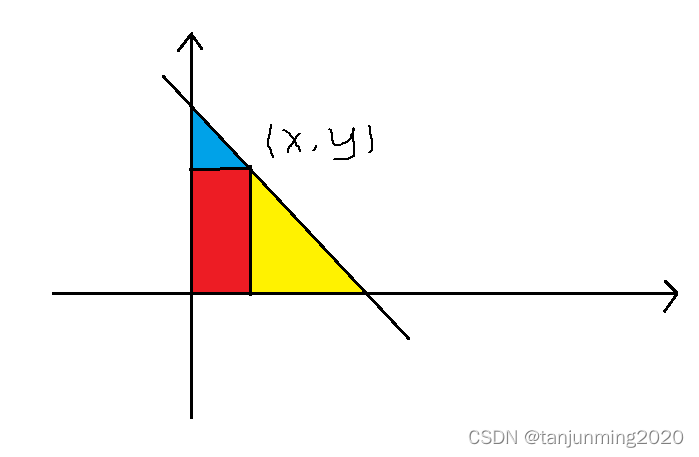
在这里插入图片描述
我们查询 $x$ 方向上 $1$ 到 $x$ 的权值和，那么我们求出的部分是红色部分和蓝色部分。然后，我们减去 $y$ 方向上 $y + 1$ 到 $x + y$ 的权值和，也就是蓝色部分，这样即可得到红色部分，也就是点 $(x, y)$ 的二维前缀和了。

对于右斜的线段，我们发现每条线段上的点的 $y - x$ 是相同的，于是我们左斜着跑扫描线。对于每次修改，我们在 $x$ 方向和 $y$ 方向上都做修改。对于每次查询，设查询的点为 $(x, y)$ ，我们观察图像。

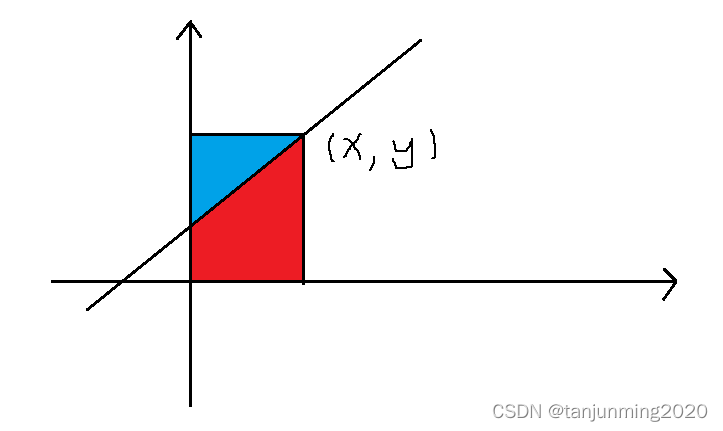
在这里插入图片描述
我们先按 $y - x$ 从小到大来操作，将修改存储在 $x$ 方向上，每次查询 $x$ 方向上 $1$ 到 $x$ 的权值和，即可得到红色部分。然后，再按 $y - x$ 从大到小来操作，将修改存储在 $y$ 方向上，每次查询 $y$ 方向双上 $1$ 到 $y$ 的权值和，即可得到蓝色部分，两者相加就是点 $(x, y)$ 的二维前缀和了。

注意在第二次操作时，对于相同的位置，要先查询再修改。因为相同位置的修改在第一次操作时已经被计算过贡献了，第二次就不需要再算贡献了。

修改和查询可以用线段树维护，时间复杂度为 $O((n+m+q)log⁡v)O((n+m+q)\log v)$ ，其中 $v$ 为坐标范围的大小。

注意

因为没有移动的矩形也算贡献，所以可以在一开始将所有矩形都算一次贡献，每次移动就不用算最开始的矩形的贡献。算一开始每个矩形的贡献可以看作矩形从它左边一个单位的位置往右移一个位置到原来的位置，这样统计的就是矩形原本的位置
虽然坐标范围是 $1$ 到 $250000$ ，但差分时会有一些点超出坐标范围，然而不会超出太多，所以我们只需要再线段树上将范围开大一点点，比如 $1$ 到 $250005$

code

#include<bits/stdc++.h>
#define lc k<<1
#define rc k<<1|1
using namespace std;
const int N=250005;
int n,m,q;
int dx[8]={1,1,0,-1,-1,-1,0,1},dy[8]={0,1,1,1,0,-1,-1,-1};
long long ans[N+5];
struct vt{
	int dx,dy,ux,uy;
}w[N+5];
struct line{
	int x,y,t,z,que;
};
struct tree{
	long long tr[4*N+5],ly[4*N+5];
	void build(int k,int l,int r){
		tr[k]=ly[k]=0;
		if(l==r) return;
		int mid=l+r>>1;
		build(lc,l,mid);
		build(rc,mid+1,r);
	}
	void down(int k,int l,int r){
		int mid=l+r>>1;
		tr[lc]+=ly[k]*(mid-l+1);
		tr[rc]+=ly[k]*(r-mid);
		ly[lc]+=ly[k];
		ly[rc]+=ly[k];
		ly[k]=0;
	}
	void ch(int k,int l,int r,int x,int y,long long z){
		if(l>=x&&r<=y){
			tr[k]+=(r-l+1)*z;ly[k]+=z;
			return;
		}
		if(ly[k]) down(k,l,r);
		int mid=l+r>>1;
		if(x<=mid) ch(lc,l,mid,x,y,z);
		if(y>mid) ch(rc,mid+1,r,x,y,z);
		tr[k]=tr[lc]+tr[rc];
	}
	int find(int k,int l,int r,int x,int y){
		if(l>=x&&r<=y) return tr[k];
		if(ly[k]) down(k,l,r);
		int mid=l+r>>1;
		long long re=0;
		if(x<=mid) re+=find(lc,l,mid,x,y);
		if(y>mid) re+=find(rc,mid+1,r,x,y);
		return re;
	}
}tx,ty;
vector<line>v[4];
bool cmp1(line ax,line bx){
	if(ax.x!=bx.x) return ax.x<bx.x;
	return ax.que<bx.que;
}
bool cmp2(line ax,line bx){
	if(ax.x+ax.y!=bx.x+bx.y) return ax.x+ax.y<bx.x+bx.y;
	return ax.que<bx.que;
}
bool cmp3(line ax,line bx){
	if(ax.y-ax.x!=bx.y-bx.x) return ax.y-ax.x<bx.y-bx.x;
	return ax.que<bx.que;
}
void add(int p,int x,int y,int t,int z){
	if(p==0) v[p].push_back((line){y,x+1,t-1,z,0});
	else if(p==1) v[p].push_back((line){x+1,y+1,t-1,z,0});
	else if(p==2) v[p].push_back((line){x,y+1,t-1,z,0});
	else if(p==3) v[p].push_back((line){x-1,y+1,t-1,z,0});
	else if(p==4) v[p-4].push_back((line){y,x-t,t-1,z,0});
	else if(p==5) v[p-4].push_back((line){x-t,y-t,t-1,z,0});
	else if(p==6) v[p-4].push_back((line){x,y-t,t-1,z,0});
	else v[p-4].push_back((line){x+t,y-t,t-1,z,0});
}
void pt(int p,int id,int t){
	vt &k=w[id];
	add(p,k.dx,k.dy,t,1);
	add(p,k.dx,k.uy+1,t,-1);
	add(p,k.ux+1,k.dy,t,-1);
	add(p,k.ux+1,k.uy+1,t,1);
	k.dx+=t*dx[p];k.ux+=t*dx[p];
	k.dy+=t*dy[p];k.uy+=t*dy[p];
}
void solve1(vector<line>v1){
	sort(v1.begin(),v1.end(),cmp1);
	tx.build(1,1,N);
	for(int i=0;i<v1.size();i++){
		if(!v1[i].que) tx.ch(1,1,N,v1[i].y,v1[i].y+v1[i].t,v1[i].z);
		else ans[v1[i].que]+=tx.find(1,1,N,1,v1[i].y);
	}
}
void solve2(vector<line>v1){
	sort(v1.begin(),v1.end(),cmp2);
	tx.build(1,1,N);
	ty.build(1,1,N);
	for(int i=0;i<v1.size();i++){
		if(!v1[i].que){
			tx.ch(1,1,N,v1[i].x-v1[i].t,v1[i].x,v1[i].z);
			ty.ch(1,1,N,v1[i].y,v1[i].y+v1[i].t,v1[i].z);
		}
		else{
			ans[v1[i].que]+=
				tx.find(1,1,N,1,v1[i].x)-ty.find(1,1,N,v1[i].y+1,v1[i].x+v1[i].y);
		}
	}
}
void solve3(vector<line>v1){
	sort(v1.begin(),v1.end(),cmp3);
	tx.build(1,1,N);
	for(int i=0;i<v1.size();i++){
		if(!v1[i].que) tx.ch(1,1,N,v1[i].x,v1[i].x+v1[i].t,v1[i].z);
		else ans[v1[i].que]+=tx.find(1,1,N,1,v1[i].x);
	}
	ty.build(1,1,N);
	for(int i=(int)v1.size()-1;i>=0;i--){
		if(!v1[i].que) ty.ch(1,1,N,v1[i].y,v1[i].y+v1[i].t,v1[i].z);
		else ans[v1[i].que]+=ty.find(1,1,N,1,v1[i].y);
	}
}
int main()
{
	scanf("%d%d%d",&n,&m,&q);
	for(int i=1;i<=n;i++){
		scanf("%d%d%d%d",&w[i].dx,&w[i].dy,&w[i].ux,&w[i].uy);
		--w[i].dx;--w[i].ux;pt(0,i,1);
	}
	for(int i=1,p,id,t;i<=m;i++){
		scanf("%d%d%d",&p,&id,&t);
		pt(p,id,t);
	}
	for(int i=1,x,y;i<=q;i++){
		scanf("%d%d",&x,&y);
		v[0].push_back((line){y,x,0,0,i});
		v[1].push_back((line){x,y,0,0,i});
		v[2].push_back((line){x,y,0,0,i});
		v[3].push_back((line){x,y,0,0,i});
	}
	solve1(v[0]);solve1(v[2]);
	solve2(v[3]);solve3(v[1]);
	for(int i=1;i<=q;i++){
		printf("%lld\n",ans[i]);
	}
	return 0;
}