用真值表与卡罗图设计电路

目录

【1】真值表的建立

【2】真值表转卡罗图

【3】卡罗图演化为与非门的逻辑表达式

【4】逻辑表达式构成逻辑电路图

---

【1】真值表的建立

真值表的建立依靠你想的得到的结果。例如该题：当四个输入端中有三个或四个为“1”时，输出端才为“1”。根据该题的要求，我们可以得到下图1真值表：

图1

D	0	0	0	0	0	0	0	0	1	1	1	1	1	1	1	1
A	0	0	0	0	1	1	1	1	0	0	0	0	1	1	1	1
B	0	0	1	1	0	0	1	1	0	0	1	1	0	0	1	1
C	0	1	0	1	0	1	0	1	0	1	0	1	0	1	0	1
Z	0	0	0	0	0	0	0	1	0	0	0	1	0	1	1	1

                                                                                                 

【2】真值表转卡罗图

根据图1真值表，按照Z为“1”处所对应的A、B、C、D值建立下图2塔罗图：

图2

↓BC\DA→	00	01	11	10
00
01			1
11		1	1	1
10			1

【3】卡罗图演化为与非门的逻辑表达式

按照画圈法将图2中所有的“1”包裹，包裹的大小为2^n，n为自然数，包裹的圈数量越少越好。按照该题我们就可以画出以下4个圈：

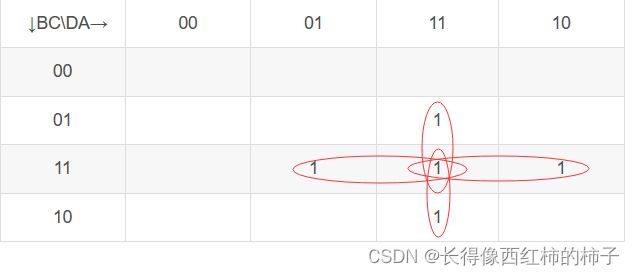
然后再相同保留，不同舍去，得到

接着再将该逻辑表达式化成与非门的形式

【4】逻辑表达式构成逻辑电路图

最后根据逻辑表达式用“与非门”构成逻辑电路图：     

                    

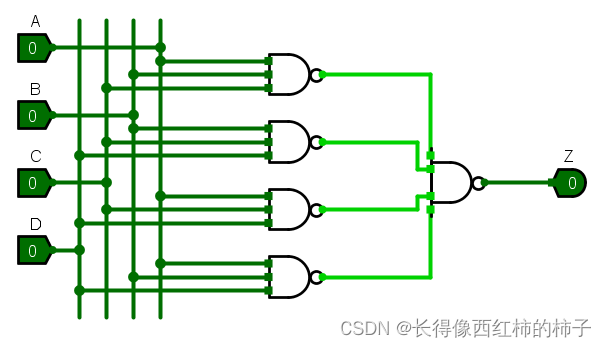
接着再设计成我们实际用的：

         

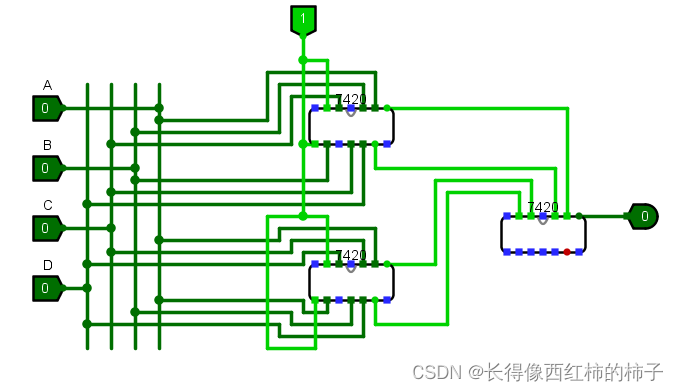
接着就可以按照这个逻辑电路图实际操作我们的器材，验证正确性。