链接中的Youtube频道对统计相关的各种概念有很好的讲解,强烈推荐。本篇简单摘要记录一下常见的分布。
这些常见分布Excel都是支持的。
Binomial
- 2 outcomes per trial, proba p or (1-p)
- Trials are independent
- Number of success/failure follows binomial distribution
Negative Binomial
“负二项分布”与“二项分布”的区别在于:“二项分布”是固定试验总次数N的独立试验中,成功次数k的分布;而“负二项分布”是所有到r次成功时即终止的独立试验中,失败次数k的分布。
Geometric
Similar to Binomial Distribution but concerns the number of trials to get the first success.
Binomial: 抓10次牌,每次抓完放回去,抓到2次红桃的概率
Geomitric:抓7次牌才遇到红桃的概率
Hypergeometric
- Just like Binomial Distribution but without replacement. 事件之间不是独立的。
Binomial: 抓10次牌,每次抓完放回去,抓到2次红桃的概率
Hyper:抓10张牌,抓到2张红桃的概率
Poisson
- Discrete
- Number of events occuring in a fixed time interval or region of opportunity (不仅仅适用于时间!)
- Events are independent
- One parameter : lambda
- >= 0
Exponential
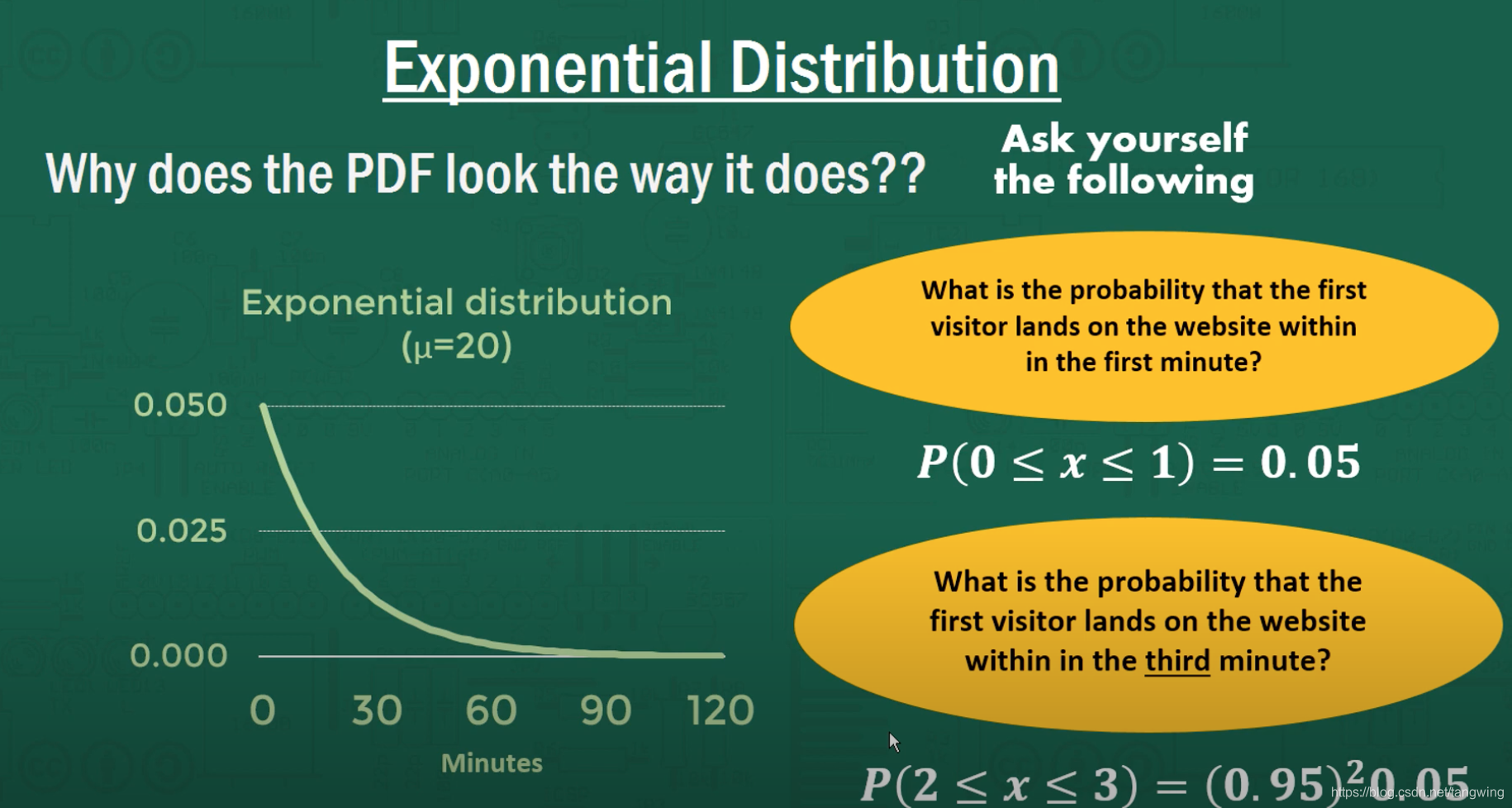
The reverse of Poisson : 相邻两次events的间隔时间。注意,需要理解为什么曲线是单调下降而不是在均值附近凸起。例如,每两辆公交车之间的等待时间符合均值为十分钟的Exponential Distribution但是曲线仍是单调的。原因可以参考下图,大意就是,公交车在第二个时间点到来的概率,隐含了公交车之前没有到来这个事实,所以需要乘上这个概率。于是有了exponential terms
Normal
这个不必多说,多样本,连续分布
T distribution/test
主要用来处理小样本的统计。数据的背后是normal distribution不过拿到的样本很少,不知道variance。
此时可以根据样本的统计值来得出对应的t distribution,以近似背后的normal distribution
更需要知道的是t-test:用来测试两个分布的mean是否相同。
F test
测试两个分布的variance是否相同。https://zhuanlan.zhihu.com/p/139151375
方差分析与ANOVA:例如在检验一个因素x的不同取值是否对指标有影响,分别令x={1,10,100},每个取值实验n次,然后看指标y的值是否有差异。此时如果x=100时y普遍比较大,我们就能得出x的取值对y比较有影响吗?不一定,由于样本的偏差,这一结果可能是偶然的,于是就需要进行方差分析,判断在当前的方差观测下,不同x的y结果是否差异显著
Chi-Square distribution
首先,可以认为是N个正态分布的平方和。符合自由度为N的卡方分布。
然后要知道卡方检验的两个主要用途:
- 拟合优度的测试:两组样本是否符合同一个distribution
- 独立性测试:一个joint distribution的多个变量是否相关





 本文介绍了统计学中的几种常见分布,包括二项分布、负二项分布、几何分布、超几何分布、泊松分布、指数分布、正态分布、T分布、F分布及卡方分布,并解释了它们的应用场景及特点。
本文介绍了统计学中的几种常见分布,包括二项分布、负二项分布、几何分布、超几何分布、泊松分布、指数分布、正态分布、T分布、F分布及卡方分布,并解释了它们的应用场景及特点。
















 2万+
2万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








