卡方分布

最新推荐文章于 2022-02-18 13:23:44 发布

翻译最新推荐文章于 2022-02-18 13:23:44 发布 · 8.3k 阅读

统计分布专栏收录该内容

5 篇文章

订阅专栏

本文深入探讨了卡方分布，包括中心卡方分布的概率密度函数及其与标准正态分布的关系，伽玛函数的概念，以及当k=2时转化为指数分布的情况。此外，还介绍了非中心卡方分布，解释了非中心参数λ的意义，并提供了随机变量的概率密度函数表达式。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

1、中心卡方分布

如果我们有 $k$ 个独立的标准正态分布随机变量 $x_1,x_2,\ldots,x_k$ ，则其平方和 $Z=\sum_{i=1}^kx_i^2$ 满足自由度为 $k$ 的卡方分布，概率密度函数为
$\tag{1} p_Z(z)=\left\{\begin{aligned} \frac{z^{\frac{k}{2}-1}e^{-\frac{z}{2}}}{2^{\frac{k}{2}}\Gamma(\frac{k}{2})}&,&z>0\\ 0&,&{\rm otherwise}. \end{aligned} \right.$
其均值为自由度 $k$ ，方差为 $2 k$ 。
下面我们首先来看看伽玛分布。

2、伽玛函数

下面我们来看看Gamma函数的定义。
$\Gamma(\alpha)=\int_{0}^{+\infty}x^{\alpha-1}e^{-x}dx,$ 如果我们令 $x=t^2$ ，则有
$\Gamma(\alpha)=\int_{0}^{+\infty}2t^{2\alpha-1}e^{-t^2}dt。$ 进一步，我们有
$\begin{aligned} &\Gamma(1)=1\\ &\Gamma(\frac{1}{2})=\sqrt{\pi}\\ &\Gamma(\alpha+1)=\alpha\Gamma(\alpha)\\ &\Gamma(n+1)=n\Gamma(n)=n! \end{aligned}$ 推荐一个关于Gamma函数的视频（https://www.youtube.com/watch?v=ixaz8-q90L8）。

3、中心卡方分布的概率密度函数曲线

//下面我们用MATLAB看下卡方分布的概率密度函数曲线。
clear;
for k=1:12
    for z1=1:1400
        z=z1/100;
        pdf(k,z1)=power(z,k/2-1)*exp(-z/2)/power(2,k/2)/gamma(k/2);
    end
end
x=0.01:0.01:14;
plot(x,pdf(1,:),'r')
hold on;
plot(x,pdf(2,:),'y')
plot(x,pdf(4,:),'g')
plot(x,pdf(6,:),'b')
plot(x,pdf(11,:),'k')

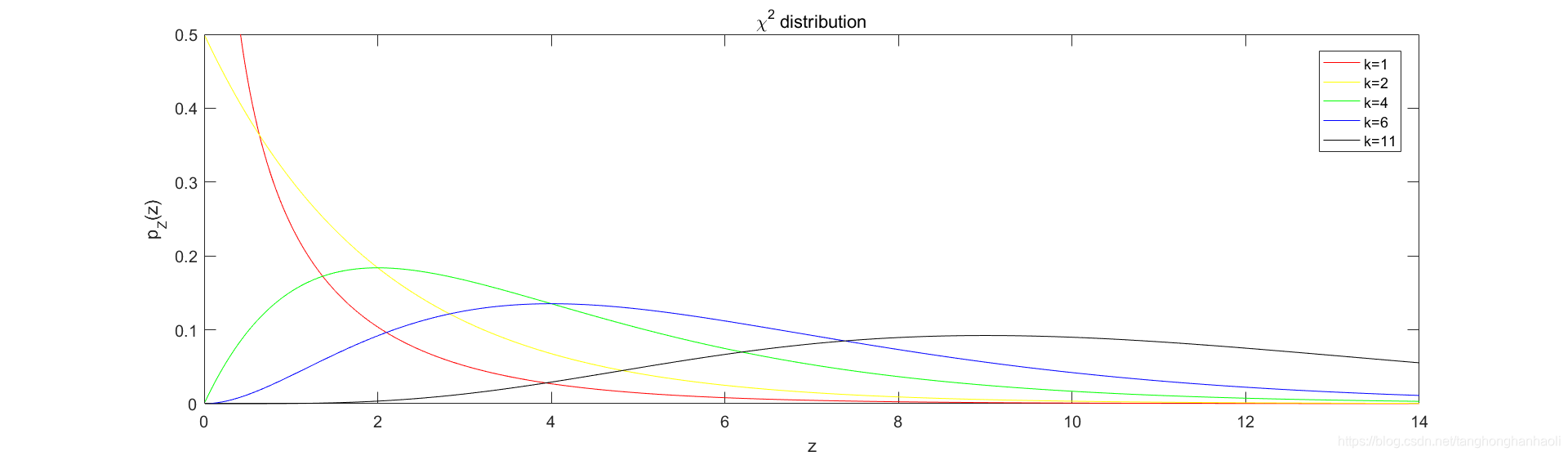
当然也可以调用MATLAB里面的函数chi2pdf(Z,k)。图1为卡方分布的概率密度函数曲线。
在这里插入图片描述

图1 卡方分布概率密度函数

4、指数分布

若 $k = 2$ ，则 $Z$ 满足指数分布，即
$\tag{2} p_Z(z)=\left\{\begin{aligned} \frac{1}{2}e^{-\frac{z}{2}}&,&z>0\\ 0&,&{\rm otherwise}. \end{aligned} \right.$

5、非中心卡方分布

令 $X_1,X_2,\ldots,X_i,\ldots,X_k$ 为 $k$ 个独立且正态分布的随机变量，其中 $X_i$ 的均值为 $\mu_i$ ，方差为1，这里 $i=1,2,\ldots,k$ ，则随机变量
$Z=\sum_{i=1}^{k}X_i^2$ 满足非中心卡方分布，它有两个参数，一个是自由度 $k$ ，另外一个参数 $\lambda$ 与随机变量 $X_i$ 的均值有关，即
$\lambda=\sum_{i=1}^{k}\mu_i^2.$ $\lambda$ 有时也被称为非中心参数。非中心卡方分布随机变量 $Z$ 的概率密度函数为
$p_Z(z)=\sum_{i=0}^{\infty}\frac{e^{\frac{-\lambda-z}{2}}(\frac{\lambda}{2})^iz^{\frac{k+2i}{2}-1}}{2^{\frac{k+2i}{2}}\Gamma(\frac{k+2i}{2})i!},$ 其均值和方差分别为
$\begin{aligned} {\rm E}(Z)&=\lambda+k\\ {\rm Var}(Z)&=2(k+2\lambda). \end{aligned}$