基于简化有序二叉决策图的组合电路多固定故障可测性分析
1 引言
当前的测试策略通常考虑单固定故障(SSAF)覆盖率。其假设是,SSAF测试集将能以满意覆盖率检测其他类型的故障,如多个固定故障和桥接故障。多固定故障模型能够捕捉未建模缺陷。若考虑除SSAF之外的独立故障模型,则会导致较长的测试计算时间。
一个包含 $n$ 条 nets 的电路可能产生 $3^n - 1$ 多 stuck-at 故障(MSAFs)。要为这些故障生成测试是不现实的。已有许多方法被提出,以实现对无扇出电路、无冗余两级电路以及内部无扇出电路的完整的多故障固定故障覆盖。但实际上,电路确实存在内部再汇聚扇出。其他研究侧重于通过映射单固定故障测试来评估多固定型故障测试。由于单固定故障测试模式 readily 可用,将其映射以检测 MSAFs 将显著减少测试生成工作量。藤田等人最新的研究涉及基于SAT的电路自动测试模式生成公式,适用于具有大量故障的电路。阿格拉瓦尔等人[2]使用分支定界算法来检测那些未被单固定故障测试检测到的多 stuck-at 故障。
然而,[7]和[2]中的方法具有指数级的测试生成复杂度。雅各布等人 [11]提出了一种方法,用于给出基于单固定型故障测试集可检测的多重故障的下限,该方法基于可保证检测或可保证检测故障(GTBD faults)。如果一个故障的检测不会因其他一个或多个故障的存在而被屏蔽,则该故障是可保证检测的。如果一个多重故障组合中的某一个故障是可保证检测的,则该多固定型故障(MSAF)也是可保证检测的。在一个具有n条线路的电路中,若可保证检测故障的数量为k,则多故障故障覆盖率的下限可推导如下:
$$
C_{\text{comb}} \geq 1 - \frac{1}{3^k}
\quad (1)
$$
这需要将单个固定故障分类为可保证检测故障和非可保证检测故障,而这反过来又需要进行多 stuck-at 故障仿真。然而,对所有多 stuck-at 故障组合进行仿真是不可能的。此外,由于覆盖率仅取决于k而与n无关,因此该指标所显示的覆盖率可能会产生严重误导。
金等人[12]提出了一种用于生成多重故障测试的另一种算法。该方法提供了一种将任意多固定故障建模为单个固定故障的流程。该方法需要插入n+3个建模门,其中n表示目标故障的重数。这使得可以通过单固定故障自动测试图生成来检测多重故障。然而,其缺点在于多重故障的故障覆盖率非常低。
对被测电路进行穷尽测试将覆盖包括多 stuck-at 故障和桥接故障在内的复杂故障,然而这并不现实。麦克卢斯基等人在[15, 16]中提出了一种称为伪穷尽测试的实用方法。该提议旨在用于内置自测试架构。伪穷尽测试策略可应用于本质上具有模块化的基于ROBDD的结构。
基于BDD的可测性综合由贝克尔[3]提出。在此工作中,大多数节点被替换为 2×1多路复用器。针对特定类别的节点提出了电路变换方法。已证明,对于某些特定类别的节点,所有路径都是强健可测的,并且仅对于这些节点,完全单个固定故障覆盖率意味着完全多固定故障覆盖率。内部电路变换有可能在电路的其余部分引入冗余。这一缺陷在德雷施勒[6]的工作中得到克服。在此工作all中,所有节点都被替换为 2×1 mutiplexers,并添加了一个额外控制输入。这使得电路具有完全的强健可测性。马特罗索娃提出了一种消除附加输入同时保持所有路径强健可测性的方法。et al. 在[14]中提出,此处将ROBDD节点替换为基于异或的子电路。尽管所有路径都是强健可测的,但 ROBDD节点深度的增加导致路径长度显著增加。在我们之前的工作[18],中,我们将异或门替换为或门,仅对连接到叶节点的节点进行电路变换。虽然失去了完全的强健可测性,但证明了存在可验证的非强健测试的条件。可验证的非强健测试与强健测试同样有效。我们已经证明所有路径均可通过强健测试或可验证的非强健测试进行测试。
在当前工作中,我们研究了基于ROBDD的综合[18]中的多固定型故障(MSAF)可测性。由于生成的电路具有结构化特性,因此可以在设计时推导出测试向量,从而无需在综合阶段之后进行自动测试模式生成(ATPG)。我们在[20]中报告了MSAF可测性分析,证明了多 stuck-at故障的可测性,并给出了测试模式数量的估计值。在[19]中我们提出了从DSOP项推导测试向量的替代方法的初步工作。在[19]中展示的方法产生了冗余测试向量 (即未能产生可区分输出的向量)。在当前的工作中,该问题已被解决并进行了详细讨论。我们还报告了几种基准电路的MSAF测试数据量和面积(门数)。
本文的主要贡献是,证明基于简化有序二叉决策图的多路复用器实现组合电路综合的完全多-stuck-at-故障可测性,并提供生成测试集的算法。
本文组织如下:第2节介绍基于ROBDD的综合。第3节对基于ROBDD的电路进行多固定型故障可测性分析。从一个 2×1多路复用器开始,建立了多固定型故障可测性的条件。扩展到整个电路,研究了多固定型故障的可测性,并提供了测试向量生成的算法。第4节给出了基于ROBDD的电路与普通电路相比的面积。列出了一组组合和时序基准电路的多固定型故障测试的测试数据量。第5节总结全文。
2 基于ROBDD的综合
描述布尔函数的方法之一是一种称为二叉决策图或 BDD的数据结构。在BDD中,每个节点都有两个后继节点,分别对应值1和0,也称为高后继和低后继。当BDD中的同构子图被合并后,得到的结果即为简化有序二叉决策图或ROBDD。每个ROBDD节点v可用公式2中的香农展开式表示。
$$
f_v = \bar{x}
i \cdot f
{\bar{x}
i}^v + x_i \cdot f
{x_i}^v
\quad (2)
$$
 简化有序二叉决策图示例
简化有序二叉决策图示例
对于简化有序二叉决策图,由于变量序是固定的,布尔函数的表示形式是规范形式。一个具有m个输出的电路将具有包含m个根节点和两个终端或叶节点(叶节点 0和叶节点1)的简化有序二叉决策图。如果内部节点被共享,则称为共享约简有序二叉决策图。在当前工作中,我们考虑单输出函数,因此采用如图1所示的单输出约简有序二叉决策图。
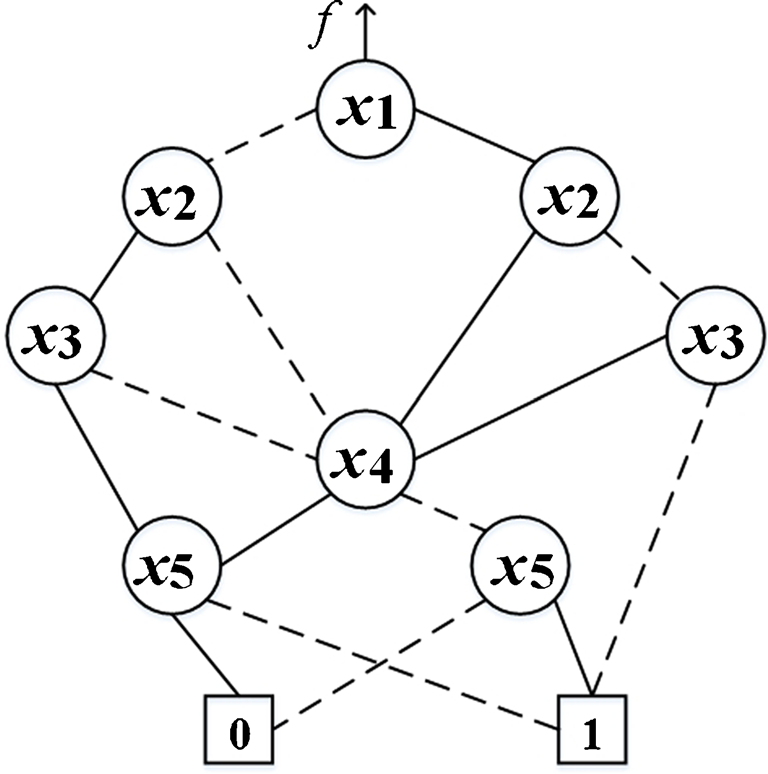
基于ROBDD的综合涉及使用决策电路实现每个节点。直观上,可以使用 2×1 mux
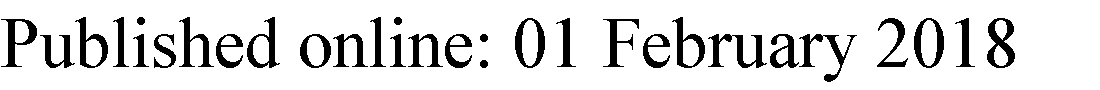 公式 $ f_v = \bar{x}
i \cdot f
{\bar{x}
i}^v + x_i \cdot f
{x_i}^v $ 的门实现
公式 $ f_v = \bar{x}
i \cdot f
{\bar{x}
i}^v + x_i \cdot f
{x_i}^v $ 的门实现
来替换每个ROBDD节点。或者,也可以使用基于异或的电路。提出了一种基于多路复用器的实现方法,旨在实现完全 PathDelay Fault可测性,如[6]所述。在该方法中,表示叶节点的附加输入t作为控制输入,用于生成信号跳变。
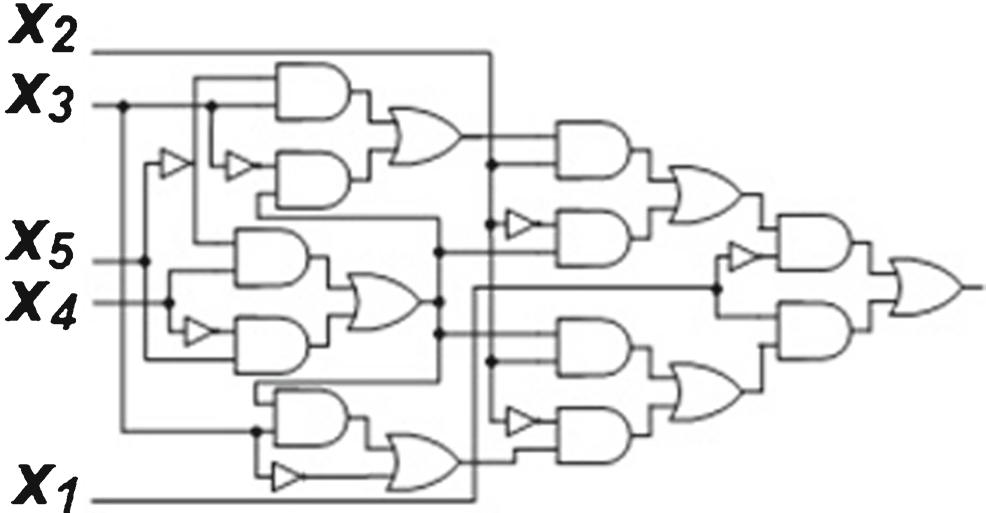
为了消除[6],连接到叶节点的节点的额外控制输入,采用了一种经过轻微修改的电路来替代 2×1多路复用器。所有中间节点均由反相-与-或子电路(2×1多路复用器)构成,如图2所示。图1中简化有序二叉决策图的复合电路如图3所示。该架构在[18]中提出,旨在实现完全路径延迟故障可测性。鲁棒和可验证的非鲁棒延迟测试能够覆盖所有路径。
在简化有序二叉决策图中,从根节点到叶节点1的每条路径对应一个积项。将从根节点到叶节点1的所有单独路径组合而成的布尔表示具有规范形式。该布尔表达式也是一种不相交积之和或DSOP[5]。因此,对于由简化有序二叉决策图表示的逻辑函数,所有单独路径构成一个不相交积之和。函数f、电路C(图3)的不相交积之和如下所示:
$$
F = x_1\bar{x}_2\bar{x}_3 + x_1\bar{x}_2x_3\bar{x}_4x_5 + x_1\bar{x}_2x_3x_4\bar{x}_5 + x_1x_2\bar{x}_4x_5 + x_1x_2x_4\bar{x}_5 + \bar{x}_1\bar{x}_2\bar{x}_4x_5 + \bar{x}_1\bar{x}_2x_4\bar{x}_5 + \bar{x}_1x_2\bar{x}_3\bar{x}_4x_5 + \bar{x}_1x_2\bar{x}_3x_4\bar{x}_5 + \bar{x}_1x_2x_3\bar{x}_5
\quad (3)
$$
不相交积之和在多重固定故障(MSAFs)的测试生成中起着关键作用。
3 多重固定故障可测性
3.1 两级与或电路的多重固定故障可测性
对电路进行穷尽测试具有两个优点:一是涵盖了包括多重固定故障、桥接故障在内的故障模型,二是测试生成工作量可以忽略不计。这将
 电路 C 对应于函数 f 在图 1
电路 C 对应于函数 f 在图 1
随着电路复杂性的增加,这种方法变得极不可行。在当前的电路C示例中,输出是5个变量的函数。由于输入变量数量非常少,包含 $2^5 = 32$ 个向量的穷尽测试集即可检测所有MSAFs。然而,当较大电路的输入数量增加时,测试向量数量急剧增长。
或者,可以将较大的电路划分为输入较少的分区,以便对这些输入进行穷尽测试[22]。这是伪穷尽测试的原理。ROBDD中的每个节点都使用一个子电路实现,这使得基于ROBDD的电路天生具有分段性。整个电路由 2×1多路复用器构成,使多路复用器成为自然的分区候选。需要敏感化从主输入到多路复用器输入以及从多路复用器输出到电路输出的路径[16]。这些路径将允许多路复用器进行穷尽测试。文献[18]已证明该电路是完全路径延迟可测的。这表明故障敏感化和传播路径易于获得。为每个多路复用器生成的测试向量驱动主输入,以敏感被测分区(一个 2×1多路复用器 对应一个节点)的故障,并将划分输出传播到电路输出。
每个ROBDD节点v的表达式为
$$
f_v = \bar{x}
i \cdot f
{\bar{x}
i}^v + x_i \cdot f
{x_i}^v
$$
由于输入为 $x_i$, $f_{\bar{x} i}^v$ 和 $f {x_i}^v$,因此需要八种组合来穷尽地测试多路复用器。$f_{\bar{x} i}^v$ 和 $f {x_i}^v$ 的值由输入变量 $x_{i+1}$ 到 $x_n$ 的组合生成。$x_i$ 是可直接驱动的主输入。对于每个ROBDD节点,以下条件中仅有一个成立。这些条件源于简化有序二叉决策图本身的结构。具体条件如下:
- $f_{\bar{x} i}^v = 0$, $f {x_i}^v = 1$ 以及 $f_{\bar{x} i}^v = 1$, $f {x_i}^v = 0$ 可以传递到该节点,或
- 仅 $f_{\bar{x} i}^v = 0$, $f {x_i}^v = 1$ 可以传递到该节点,或
- 仅 $f_{\bar{x} i}^v = 1$, $f {x_i}^v = 0$ 可以传递到该节点
已证明,如果简化有序二叉决策图的所有节点满足条件1,则电路中单重固定故障的完全可测性意味着多重固定故障的完全可测性(贝克尔 [3])。当满足 $f_{x_i}^v \not\subset f_{\bar{x} i}^v$、$f {\bar{x} i}^v \not\subset f {x_i}^v$ 和 $f_{x_i}^v \cap f_{\bar{x} i}^v = 0$ 时,存在条件1。当满足 $f {\bar{x} i}^v \subset f {x_i}^v$ 时,存在条件2;对于节点v,当满足 $f_{x_i}^v \subset f_{\bar{x}_i}^v$ 时,存在条件3。在简化有序二叉决策图中,可能存在属于这三种情况之一的节点。
这意味着无法应用全部8个值的输入组合。因此,电路中的任何多路复用器都无法进行穷尽测试。尽管无法向节点施加穷尽的值,但每个节点肯定可以施加四个值。
我们需要采用不同的方法来检测多路复用器中的所有多重故障。21 多路复用器电路是一种两级无冗余 AND-OR电路。对于无冗余的两级AND-OR网络,能够检测网络输入端所有多重固定故障的测试向量集,也将能够检测该网络的所有MSAF组合[13]。因此,如果施加到节点的四个值能够检测多路复用器输入 $x_i$, $f_{\bar{x} i}^v$ 和 $f {x_i}^v$ 处的所有多重故障,则该多路复用器的所有MSAFs都将被测试。
由于图2中的电路是两级无冗余AND-OR电路,每个乘积项都是一个质蕴涵项。如果其中一个变量固定为0,则整个项消失,产生消失故障或a-故障 [13]。如果一个变量固定为1,它将从乘积项中消失,产生收缩或b-故障 [13]。
引理1 连接到 $x_i$ 的门输入上的单个固定故障等效于 2 × 1 mux 子电路的多个 a,b-故障
证明
对于 2×1 mux(如图2所示),输入 $x_i$ 上的固定为1故障对应于多个a,b-故障 ,原因如下:
1. 方程1的第一个乘积项由于文字 $\bar{x}_i$ 变为常数0而消失(a-故障)。
2. 文字 $x_i$ 在公式的第二个乘积项中消失,因为它是常数1(b-故障)。
类似地,输入 $x_i$ 处的固定为0故障也对应于多重a,b-故障 ,如下所示:
1. 公式中第一个乘积项中的文字 $\bar{x}_i$ 消失。
2. 由于 $x_i$ 被强制为常数0(a-故障),第二个乘积项消失。
因此得证。
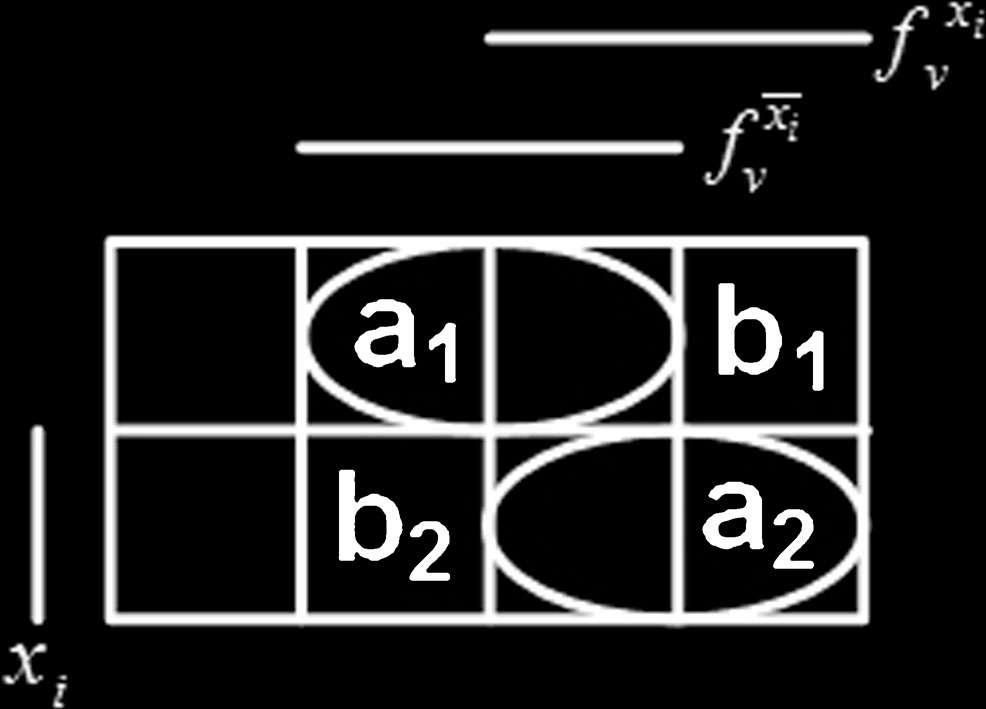
 a,b测试 用于条件1
a,b测试 用于条件1
引理2 一个能够检测子电路输入($x_i$,$f_{\bar{x} i}^v$,$f {x_i}^v$)处所有 a,b故障的测试向量集将能够检测该子电路的所有多重故障。
证明 由引理1可知,单个固定故障会导致文字的消失 (b-故障)或乘积项的消失(a-故障)。由于式(1)表示一个非冗余和积式,所有项均为质蕴涵项。要测试乘积项是否消失,只需测试该本身为质蕴涵项的乘积项即可。因此,式(1)中的两项将检测与门输入处的所有s-a-0故障(称为a-测试)。如果乘积项中的某个文字因s-a-1故障而消失,则该乘积项在缺少该文字的情况下实现。紧邻该乘积项且具有该文字补值的子立方体将检测此故障(b-测试)。集合a,b-测试 将检测子电路输入处的所有多stuck-at故障。因此,该子电路的所有多stuck-at故障均被检测到[13]。
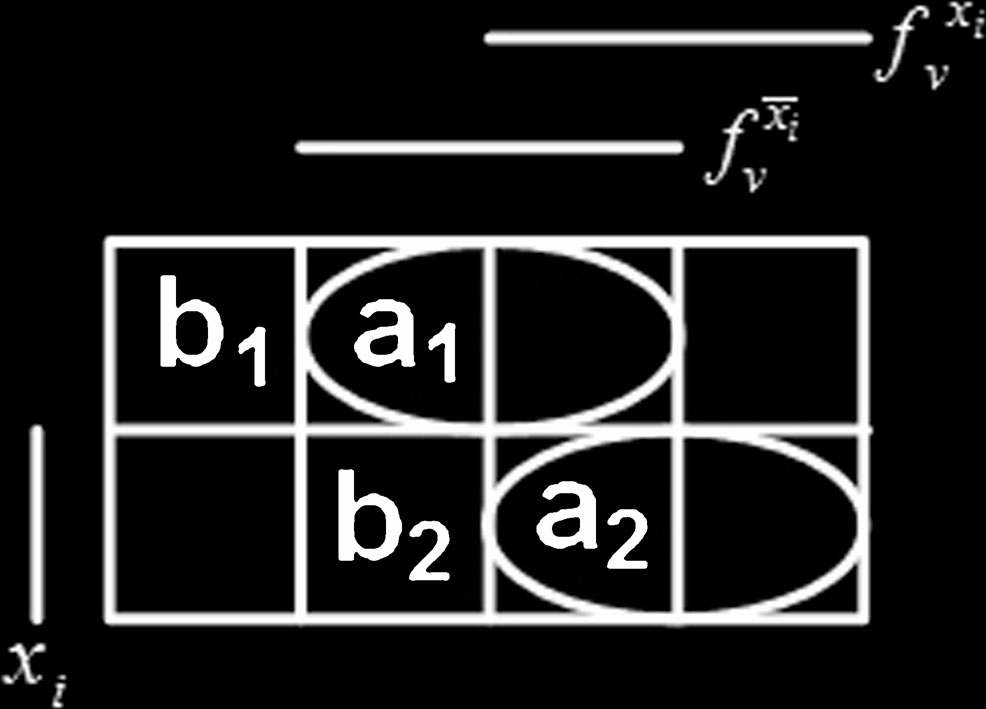
 a,b测试 用于条件2
a,b测试 用于条件2
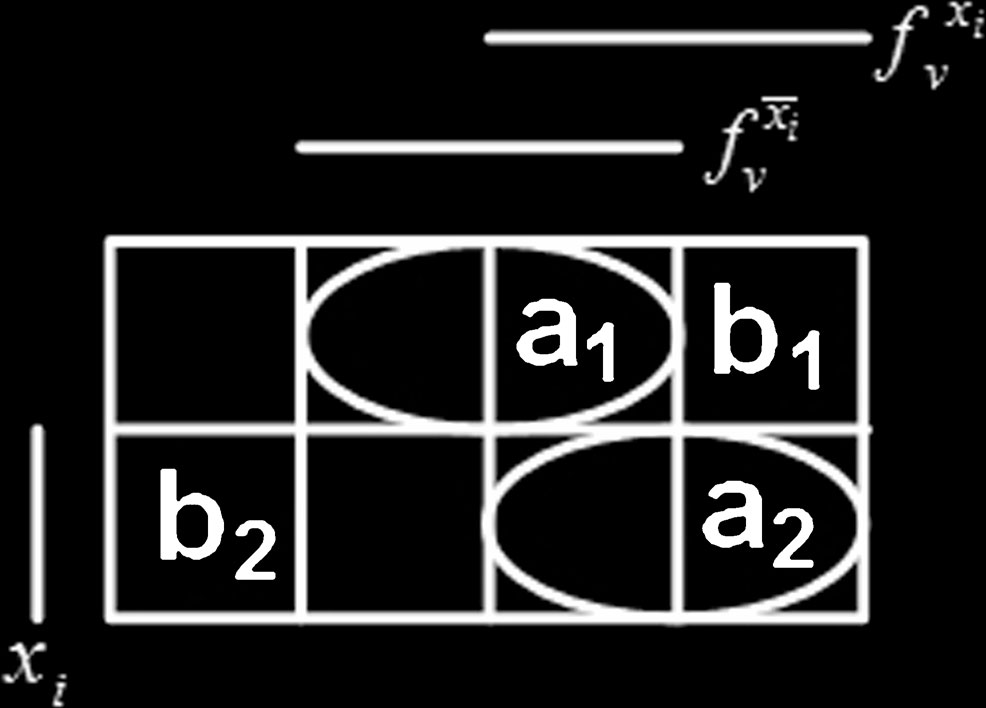
 a,b测试 用于条件3
a,b测试 用于条件3
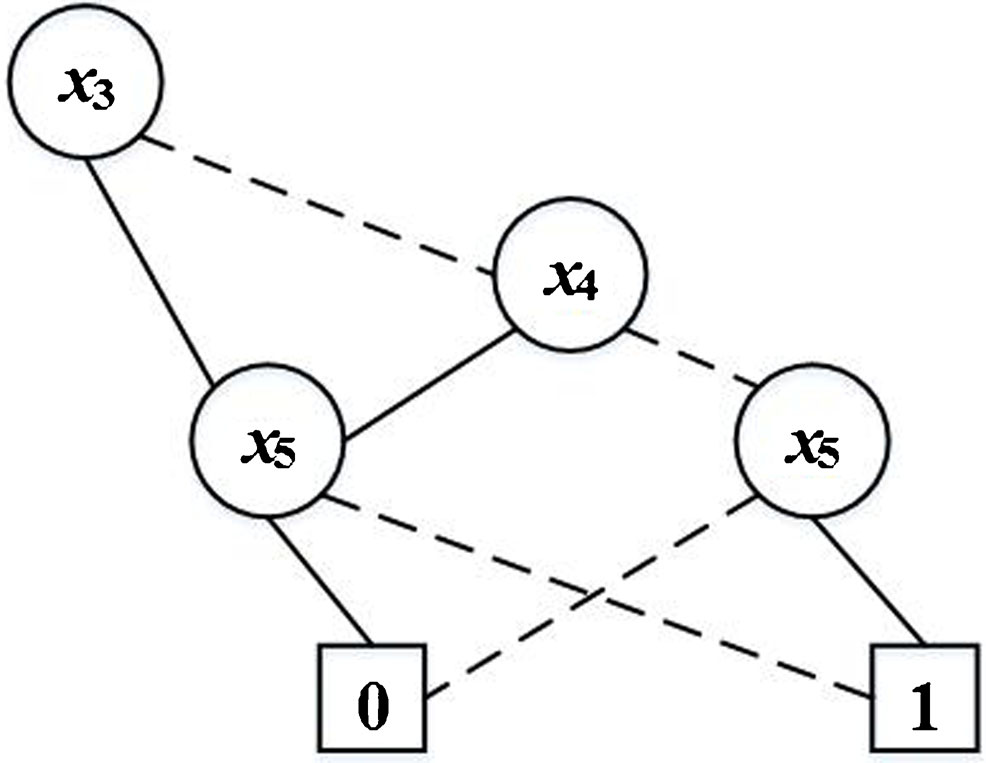
 用于 $x_3$ 的简化有序二叉决策图
用于 $x_3$ 的简化有序二叉决策图
3.2 为每个节点推导多固定型故障测试集
根据第3.1节讨论的条件,每种情况的a,b-测试集如下:
- 当 $f_{\bar{x} i}^v = 0$、$f {x_i}^v = 1$ 以及条件 $f_{\bar{x} i}^v = 1$、$f {x_i}^v = 0$ 成立时,a,b测试集为 $(x_i, f_{x_i}^v, f_{\bar{x}_i}^v) = {001, 010, 101, 110}$,如图4所示。
- 仅当条件 $f_{\bar{x} i}^v = 0$、$f {x_i}^v = 1$ 成立时,a,b测试集为 $(x_i, f_{x_i}^v, f_{\bar{x}_i}^v) = {000, 001, 101, 111}$,如图5所示。
- 仅当条件 $f_{\bar{x} i}^v = 1$、$f {x_i}^v = 0$ 成立时,a,b测试集为 $(x_i, f_{x_i}^v, f_{\bar{x}_i}^v) = {010, 011, 100, 110}$,如图6所示。
接下来的两个小节描述了两种为多 stuck-at 故障推导测试向量集的方法。
3.3 方法1:基于BDD操作的算法为每个划分推导测试向量集
这里讨论的方法与贝克尔[3]中描述的方法类似,其中针对细胞故障模型进行测试生成。我们详细阐述了 MSAF测试的一般方法。
每个ROBDD节点对应一个包含一个 2×1 mux的划分。一个有效的测试向量K必须包含
| 测试向量图号 | 所需简化有序二叉决策图 |
|---|---|
| a 2 | 图 4和 6 简化有序二叉决策图 ( $f_{x_i}^v$ ) |
| a 2 | 图 5 简化有序二叉决策图 ( $f_{\bar{x}_i}^v$ ) |
| a 1 | 图 4和 5 简化有序二叉决策图( $\bar{f} {\bar{x}_i}^v$ )*简化有序二叉决策图( $\bar{f} {x_i}^v$ ) |
| b 2 | 图 6 简化有序二叉决策图 ( $\bar{f} {\bar{x}_i}^v$ ) *简化有序二叉决策图 ( $\bar{f} {x_i}^v$ ) |
– 一个产品术语Kα,用于激划分输入。– 一个产品术语Kε,通过路径 ε将划分输出传播到电路输出。– 表示该划分的主输入 $x_i$
设 $K_\alpha x_i)\bar{x} i)K \varepsilon$ 为在多路复用器输入处的多重故障在电路C输出端表现出的复合测试模式。使该乘积变为1的布尔向量必须包含在该多路复用器的划分测试中。
当 $f_{\bar{x} i}^v = f {x_i}^v$ 恒为真时,查找分区测试向量的步骤如下。设有两个向量 γ 和 δ,使得 $f_{\bar{x} i}^v( \gamma ) = 0 $, $x_i = 1 $, $f {x_i}^v( \delta ) = 1 $, $x_i = 0 $, $ \delta \subseteq \gamma $, ${,}K_\alpha$。
从多路复用器输出函数到电路输出可能存在多条路径,即从表示分区的节点到根节点。$K_\varepsilon$ 是所有此类路径的集合。可从中选择任意一条路径。
获取 γ 以生成测试向量a2和b1的算法如图4所示:
-
ROBDD($f_{x_i}^v$) 表示针对给定内部节点 v 的函数 $f_{x_i}^v$ 的简化有序二叉决策图。其根节点是粗边($x_i = 1$) 所指向的内部节点 v。
简化有序二叉决策图($f_{\bar{x} i}^v$)的根是虚线边($\bar{x}_i$)从v出发所指向的内部节点。简化有序二叉决策图($f {x_i}^v$)和简化有序二叉决策图($f_{\bar{x}_i}^v$)的终端节点与函数f在电路 C相应输出上的简化有序二叉决策图的终端节点重合。 -
为获得 ROBDD($\bar{f} {\bar{x}_i}^v$),交换 ROBDD($f {\bar{x}_i}^v$) 的终端节点,即将叶节点0替换为叶节点1,反之亦然
-
将 ROBDD($f_{x_i}^v$) 与 ROBDD( $\bar{f}_{\bar{x}_i}^v$) 相乘,令 ROBDD R* 表示结果。
-
如果 ROBDD R 非空,则从 R 根节点到其终止节点1的路径由乘积 γ 表示。
注意,满足条件 $f_{\bar{x} i}^v(\delta)=1$ 和 $f {x_i}^v(\delta)= 0$ 的向量 δ 以类似方式计算,即通过将 ROBDD($f_{\bar{x} i}^v$) 与 ROBDD( $\bar{f} {x_i}^v$) 相乘得到。因此,图 4 中所示的所有测试模式,对应于条件 $f_{\bar{x} i}^v( \gamma ) = 0 $, $x_i = 1 $, $f {x_i}^v(\gamma)$ 和 $f_{x_i}^v(),f_{\bar{x}_i}^v()$,均可由此导出。
示例 让我们考虑图x3 1的左侧中标记的节点。1。该节点对应的 $x_3$ 的简化有序二叉决策图如图7所示。对于此节点,条件1成立。
使用上述算法为标记为$x_3$的节点(相对于图4)推导出的测试向量集如下:
$$
{a2, b1, a1, b2} = {\bar{x}_1x_2x_3\bar{x}_4\bar{x}_5, \bar{x}_1x_2\bar{x}_3\bar{x}_4\bar{x}_5, \bar{x}_1x_2\bar{x}_3\bar{x}_4x_5, \bar{x}_1x_2x_3\bar{x}_4x_5}
\quad (4)
$$
表 1 显示了计算包含条件 $f_{x_i}^v \subset f_{\bar{x} i}^v$ 和 $f {\bar{x} i}^v \subset f {x_i}^v$ 的剩余测试向量所需的 ROBDDs。对于每个条目,从根节点到终端1节点的路径表示对应的测试向量。
测试集 ${a1,a2,b1,b2}$ 是划分(伪穷尽)测试集。该测试集足以检测被测分区中所有非冗余多重故障(2×1 mux)。该方法的测试生成复杂度为$O(|C|^3)$[3],,其中 C是BDD电路规模。
 函数 f 的卡诺图
函数 f 的卡诺图
(a) (b)
 为一条路径生成b-测试集
为一条路径生成b-测试集
基于简化有序二叉决策图的组合电路多固定故障可测性分析(续)
3 多重固定故障可测性(续)
3.4 方法2:基于不相交积之和操作的测试向量集推导方法
从根节点到终止节点1的每条路径构成了不相交积之和或ROBDD的DSOP表达式的2列出了图1中ROBDD以及图3中相应电路的DSOP项。这些项可以通过卡诺图进行图形化表示,如图8a和b所示。
根据图4、图5和图6,b‐测试仅仅是a‐测试的单比特取反。有效的b‐测试需要与所有a‐测试正交。为了获得b‐测试,我们需要逐一对每个DSOP项中的比特进行取反。这可以通过矩阵来实现。对于具有n个文字的电路,我们创建一个大小为n × n的b‐测试生成矩阵 G,如图9所示。这是一个单位矩阵,其每一行在递增的位置上有一个取反的比特。D是由一个DSOP项组成的一个列矩阵。对G和D进行按位异或操作将得到对应于每个文字的b‐测试,如图10所示。
总共ab-测试=所有a-测试,即所有DSOP项 + 所有b-测试,即每个DSOP项生成的b-测试之和。
例1 让我们考虑表2中第8项中的不相交积之和项,即 $\bar{x}_1x_2\bar{x}_3\bar{x}_4x_5$。b测试的生成如图11所示。b测试列表中最后两个条目对应于某些其他的a‐测试。这可以通过图8a的卡诺图来验证。
这意味着该不相交积之和项无法为 $\bar{x}_1x_2$ 生成b‐测试。由于项 $\bar{x}_1x_2$ 存在于第9项和第10项中,因此可以从中生成有效的b-tests。此例表明,每次生成一组 b-tests时都必须检查冗余。
一种用于推导无冗余积之和的最小b-测试的方法在 [13]中被提出。针对基于ROBDD的DSOP表示电路所推导出的b-测试并非最小,因为每个变量代表一个子电路。在基于ROBDD的系统中,需要额外的步骤来消除冗余。
设P表示DSOP项集合。推导基于ROBDD的设计的 b‐测试b-tests B的步骤如下:
- 对于P中的每一项,推导出 $B^*_{jk}$ ∀j = 1, 2, · · · , m 和 k = 1, 2, · · · , r_j,其中m是不相交积之和项的数目,r_j是每项中文字的数目。这通过将每个不相交积之和项与n × n单位矩阵进行异或操作完成,n为电路的输入文字数目。
- 对于每一个 $B^ _{ab} \supseteq B^ {jt}$,从列表中移除 $B^ _{ab}$。每个对 $B^ {jt}$ 的测试都是对 $B^*_{ab}$ 的测试,但其逆命题不成立。这给出了有效b‐测试的数量。
- 在更新后的 $B^ _{jk}$ 中,用所有组合填充无关项,得到 $B^ _x$。
- 对于 $B^ _y \subset P$ 中的每一项,从 $B^ _y$ 中删除 $B^ _x$。这将消除 $B^ _x$ 中与任何不相交积之和项匹配的项。
- 对于 $B^ _{jk}$ 中的每一项,从 $B^ x$ 中保留一项,使得 $B^ _{jk} \supset B^ {ab}$。这将成为完全指定的有效b‐测试的列表。
这可以在设计周期的早期阶段完成,因为DSOP项在设计时即可获得。需要注意的是,这种测试生成策略仅适用于基于ROBDD的设计。
示例2 考虑DSOP列表中的项10,即 $\bar{x}_1x_2x_3\bar{x}_5$,即 011‐0。该术语的b‐测试在图12中得出。
在Bx矩阵中,以粗体突出显示的项是与其他 DSOP项匹配并被消除的项。在Bx(更新后)矩阵中,以斜体突出显示的项是对应于同一变量的测试,因此可以保留其中任意一个。该DSOP项本身的a测试 = 为 01100 或 01110。ab测试 集对于此DSOP项是 {01100,01101, 01000, 00100, 11100}。
 b测试 针对一个不相交积之和项的测试集
b测试 针对一个不相交积之和项的测试集
该方法的测试生成复杂度为$O(m×n)$,其中m是 DSOP项的数量,n是主输入的数量。
步骤1后导出的测试集也可用于获取检测延迟故障所需的测试向量对。在[18]中表明,检测路径延迟故障所需的转换是通过电路输入产生的,不需要附加输入。在基于ROBDD的设计中,控制路径的文字是输入变量。可以通过应用一个包含该路径的产品术语以及相关文字取互补值的测试向量对,来测试从某一文字开始的子路径[18]。路径延迟测试集是MSAF测试的超集。
通过合并所有部分测试集并消除冗余而得到的完整测试集能够检测所有多重固定故障。单重固定故障是多 stuck-at 故障的一部分,可被自动覆盖。
具有N个节点的简化有序二叉决策图将有N个分区,因此需要4N个测试向量来测试整个电路。生成测试向量所需的ROBDD或DSOP操作可以在多项式时间内完成。注意,实际所需的测试向量数量少于4N。
假设每个子电路的测试集为{a1, a2, b1, b2},测试向量a1, a2表示 $\bar{x} i·f {\bar{x} i}^v + x_i·f {x_i}^v$。这些项是不相交积之和(DSoP)的子集。每个DSoP项对应于一条单独路径,并且将包含该路径上所有节点的a‐测试之一。
设路径 p 表示一个 DSoP 项。设在路径 p 上遇到的节点数量为 m。一个 a测试对所有p中的节点而言是共通的。每个节点位于两条路径上,一条由 $x_i$ 控制,另一条由 $\bar{x}_i$ 控制。这意味着对于每个节点,还存在另一个DSoP项(即另一个a-测试)。因此,对于路径p,测试向量的数量为2m + m = 3m,其中2m是b-测试的数量,而m是a-测试的数量。这对电路中的所有节点均成立。因此,最多需要施加3N个测试向量来检测所有MSAFs,其中N为ROBDD节点计数。
3.5 所提方法的MSAF检测
已在第3.1节中指出,基于ROBDD的实现中的每个子电路被视为一个分区,并且可使用敏感化分区方法 [16] 对多重故障进行测试。每个分区的ab测试集可通过第3.3节中描述的方法或第3.4节中描述的方法获得。
在ROBDD中,文字的秩是已知且固定的。由于每个节点对应一个主输入,因此主输入的秩是已知的。不失一般性,输入变量的秩取为 $x_1,....,x_{n−1},x_n$,其中 $x_1$ 是根节点,且秩最高。
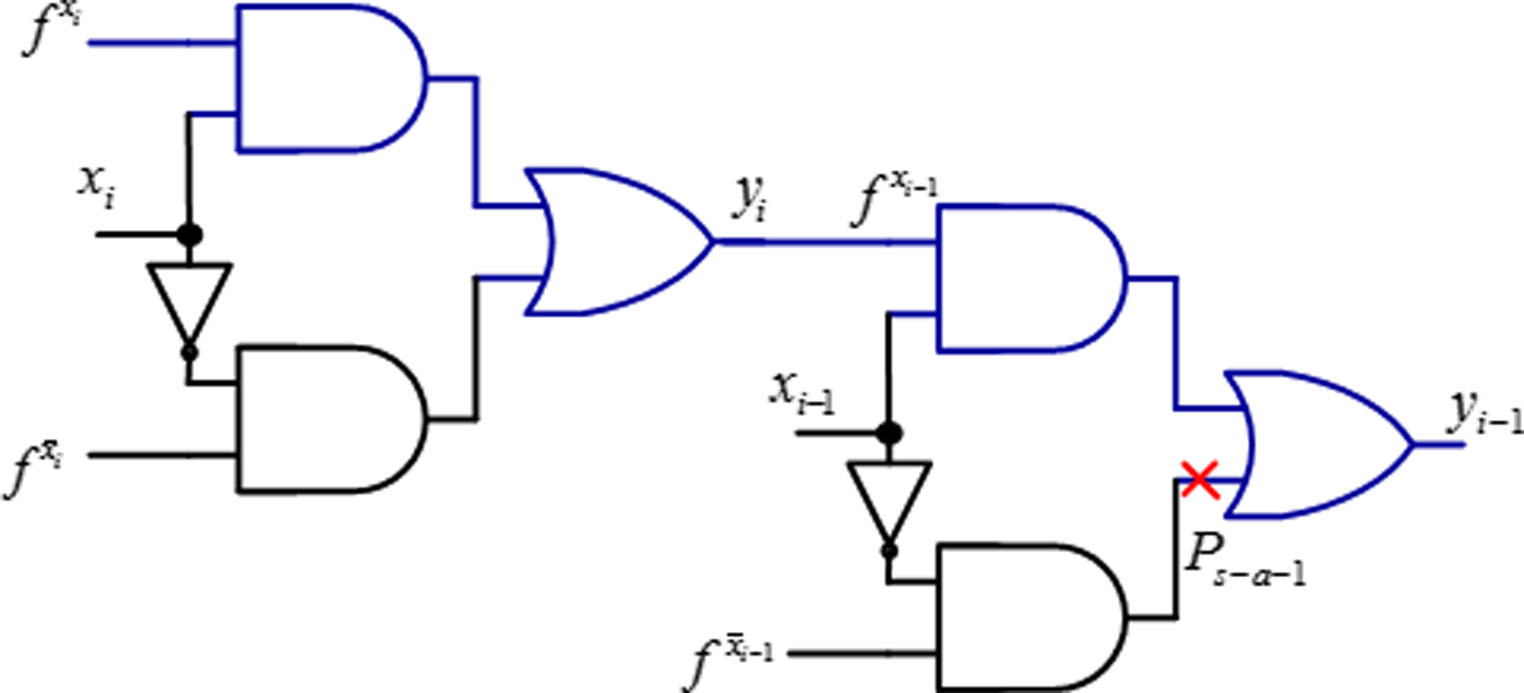
定理1 一个由秩为i的变量控制的多路复用器的b-测试向量能够检测所有由秩大于i的变量所控制的分区的关断路径上的固定为1的故障。
证明 考虑如图13中的一个通用电路。设h为穿过由 $x_i$ 和 $x_{i−1}$ 分别控制的多路复用器的路径。我们假设该电路按照从低秩到高秩的变量顺序进行测试。仅当 $x_i$ 处的多路复用器被发现无故障时,才会测试由 $x_{i+1}$ 控制的多路复用器。因此,概括地说,所有由秩小于i的变量控制的多路复用器均被假定为无故障。
由针对受 $x_i$ 控制的多路复用器生成的分区测试集中的任何测试向量都将在多路复用器输出 $y_i$ 处产生 D 或 $\bar{D}$。该测试向量还通过向 $x_{i−1}$(本例中为1)施加必要值,确保 $y_i$ 根据路径h的秩传播到下一级电路。如果由 $x_{i−1}$ 控制的多路复用器是无故障的,则D或$\bar{D}$将被传播到 $y_{i−1}$。位置P位于关断路径上。此处可能存在固定为1故障,该故障可能是由于实际的固定故障,或是由于表示 $\bar{x} {i−1}$ 的电路中的多重故障所致。$f {\bar{x}_{i−1}}$。当 $\bar{y}$ 的值为 $y_i$ 时为D或$\bar{D}$的情况下可能出现的情况如表3所示。
对于由变量 $x_i$ 标记的电路,当应用a测试时,$y_i$ 处的输出将为D。这将被P s−a−1故障所屏蔽。然而,一个b测试将生成$\bar{D}$。在这种情况下,P s−a−1将通过其中一个测试在输出端传播,电路将被检测为存在故障。因此,针对由变量 $x_i$ 控制的子电路的测试向量将能够检测到所有由秩大于i的变量所控制的多路复用器在其关断路径上存在的固定为1故障,这些变量位于路径h上。该结论适用于路径 h上的所有关路径上的固定为1故障。因此,应按照变量秩从低到高的顺序对所有多路复用器进行测试。此测试策略将检测电路中的所有故障。证毕。
如果线路P固定为0,则它对或门起到非控制值的作用。D或$\bar{D}$值将从上一级电路在变量等级递增的情况下传播到下一级电路。当应用专为该故障所在分区设计的a测试时,此P s−a−0故障将被检测到。
引理3 对于基于ROBDD的实现,如果按照ROBDD变量顺序 $x_n,x_{n−1}$,....$x_1$, 提供划分测试,则可以检测被测电路的所有非冗余多重故障。
证明 设当前正在测试的分区由 $x_i$ 控制,其中 $n > i > 1$。秩小于j($i > j > 1$)的变量所对应的多路复用器的故障可能会影响秩为i的多路复用器的故障传播至电路输出。此时可能产生故障输出,也可能因故障被屏蔽而产生无故障输出。若产生故障输出,则测试将停止。如果秩为i的多路复用器的故障传播被另一个秩更高的多路复用器的故障所屏蔽,则秩j的测试将继续进行。由于测试是按照变量秩从低到高进行的,因此在变量秩j处的故障最终将由其对应的a,b测试进行测试并被检测到。因此,按照ROBDD变量顺序 $x_n, x_{n−1}, · · · , x_1$ 施加的测试将检测电路中的所有非冗余多重故障。
4 面积与测试向量计算
对于基于ROBDD的实现,需要指导综合工具避免优化,以保持结构。我们使用ABC工具[4]生成基于BDD 的电路并进行综合。为了进行面积比较,采用了 gscl45nm库。
A Python程序用于实现推导部分测试向量集(方法2)和完整MSAF测试向量集的算法。ROBDD设计的未优化综合和SSAF仿真通过ABC完成。针对若干组合基准电路,表4给出了有关测试向量和逻辑门数量的数据。第一列指明了所考虑的基准电路。下一列指明了电路的原始输入(PIs)和输出(POs)。第3列和第4列分别列出了ROBDD项和对应的DSOP项。第5列列出了SSAF测试数量,第6列列出了MSAF测试。
需要注意的是,推导出多 stuck-at 故障的电路具有多个输出。所有输出在其扇入锥中并非包含所有输入。如果为所有输出考虑全部输入,则第3.4节中步骤3的x填充过程可能呈指数级增长,特别是对于时序电路。因此,在生成b-测试时,每次仅考虑一个输出及其对应的输入。该过程对所有输出重复进行。
由于无法对多 stuck-at 故障(MSAFs)进行故障仿真,因此无法实现测试压缩。结果,对于大多数电路而言,MSAF的测试数据量比单固定型故障(SSAF)的测试数据量更大。然而,如果对基于 ROBDD的设计进行未优化的综合,则在设计时生成的测试是综合后电路的有效MSAF测试。
| 组合的 | 输入端口/输出端口 | ROBDD节点 | DSOP项 | SSAF测试 | MSAF测试 | 基区域 (逻辑门) | BDD面积 (逻辑门) |
|---|---|---|---|---|---|---|---|
| b1 | 3/4 | 6 | 6 | 5 | 10 | 13 | 12 |
| C17 | 5/2 | 9 | 7 | 7 | 6 | 6 | 8 |
| 解码 | 5/16 | 80 | 16 | 17 | 48 | 22 | 46 |
| rd53 | 5/3 | 21 | 35 | 12 | 34 | 32 | 45 |
| xor5 | 5/1 | 5 | 16 | 10 | 32 | 16 | 26 |
| cm138a | 6/8 | 48 | 48 | 10 | 7 | 17 | 22 |
| 5xp1 | 7/10 | 83 | 74 | 21 | 81 | 75 | 126 |
| con1 | 7/2 | 16 | 9 | 11 | 15 | 9 | 23 |
| rd73 | 7/3 | 35 | 147 | 28 | 132 | 141 | 121 |
| z4ml | 7/4 | 28 | 59 | 15 | 55 | 20 | 52 |
| f51m | 8/8 | 58 | 78 | 40 | 94 | 43 | 150 |
| misex1 | 8/7 | 61 | 33 | 18 | 28 | 32 | 66 |
| mm4a | 8/4 | 439 | 508 | 184 | 1203 | 146 | 911 |
| rd84 | 8/4 | 50 | 294 | 28 | 273 | 256 | 157 |
| sqrt8 | 8/4 | 39 | 42 | 22 | 49 | 93 | 64 |
| 9sym | 9/1 | 24 | 148 | 29 | 138 | 43 | 74 |
| clip | 9/5 | 141 | 150 | 66 | 191 | 167 | 182 |
| ldd | 9/19 | 142 | 61 | 42 | 38 | 117 | 93 |
| alu2 | 10/6 | 177 | 156 | 131 | 322 | 335 | 386 |
| x2 | 10/7 | 46 | 28 | 21 | 28 | 42 | 53 |
| sao2 | 10/4 | 116 | 75 | 43 | 173 | 58 | 154 |
| cm85a | 11/3 | 50 | 48 | 19 | 118 | 38 | 55 |
| cm151a | 12/2 | 36 | 17 | 24 | 43 | 111 | 22 |
| alu4 | 14/8 | 760 | 635 | 480 | 1425 | 681 | 850 |
| cu | 14/11 | 78 | 22 | 32 | 64 | 48 | 57 |
| misex3 | 14/14 | 871 | 1306 | 272 | 1972 | 1848 | 1034 |
| cm163a | 16/5 | 35 | 27 | 21 | 29 | 42 | 52 |
| cmb | 16/4 | 48 | 26 | 18 | 30 | 41 | 43 |
| pdc | 16/40 | 4706 | 6062 | 230 | 2026 | 2406 | 3772 |
| pm1 | 16/13 | 62 | 37 | 17 | 45 | 104 | 52 |
| t481 | 16/1 | 30 | 481 | 51 | 630 | 2072 | 110 |
| 表5 | 17/15 | 1819 | 551 | 308 | 1247 | 733 | 1651 |
| tcon | 17/16 | 24 | 24 | 17 | 21 | 41 | 33 |
| vda | 17/39 | 1161 | 573 | 125 | 322 | 585 | 1101 |
| pcle | 19/9 | 107 | 45 | 29 | 90 | 68 | 84 |
| sct | 19/15 | 124 | 73 | 35 | 92 | 162 | 88 |
| cc | 21/20 | 88 | 45 | 26 | 50 | 47 | 62 |
| cm150a | 21/1 | 32 | 17 | 24 | 52 | 69 | 33 |
| duke2 | 22/29 | 642 | 201 | 143 | 357 | 87 | 527 |
| cordic | 23/2 | 90 | 1180 | 57 | 6604 | 102 | 128 |
| ttt2 | 24/21 | 243 | 138 | 59 | 227 | 200 | 183 |
| i1 | 25/13 | 59 | 27 | 26 | 44 | 46 | 62 |
| vg2 | 25/8 | 269 | 110 | 155 | 293 | 434 | 154 |
| lal | 26/19 | 146 | 102 | 60 | 115 | 114 | 136 |
| pcier8 | 27/17 | 153 | 61 | 51 | 100 | 84 | 112 |
| c8 | 28/18 | 116 | 79 | 43 | 102 | 164 | 119 |
| frg1 | 28/3 | 103 | 119 | 96 | 172 | 105 | 49 |
| 术语1 | 34/10 | 227 | 255 | 122 | 780 | 358 | 178 |
| 计数 | 35/16 | 200 | 184 | 73 | 209 | 143 | 224 |
| 未注册 | 36/16 | 96 | 48 | 48 | 68 | 97 | 116 |
| b9 | 41/21 | 220 | 138 | 84 | 176 | 125 | 111 |
| seq | 41/45 | 2536 | 1467 | 424 | 2472 | 2951 | 2150 |
| cht | 47/36 | 181 | 81 | 71 | 110 | 229 | 119 |
| x1 | 51/35 | 671 | 304 | 337 | 817 | 285 | 310 |
| e64 | 65/65 | 2144 | 65 | 97 | 2082 | 65 | 805 |
| example2 | 85/66 | 746 | 367 | 237 | 796 | 277 | 377 |
| x4 | 94/74 | 628 | 526 | 270 | 1008 | 369 | 368 |
| o64 | 130/1 | 130 | 65 | 69 | 81 | 65 | 129 |
| x3 | 135/99 | 1070 | 657 | 393 | 1737 | 715 | 723 |
| i6 | 138/67 | 613 | 238 | 220 | 214 | 340 | 524 |
时序电路由于存在触发器,除了主输入和主输出外,还有伪主输入(PPIs)和伪主输出(PPOs)。时序电路中的ROBDD构建会考虑PPIs和PPOs。表5列出了某些时序基准电路的数据。
| 时序 | 输入端口/输出端口 | PI+PPI/PO+PPO | Robdd节点 | DSOPs | SSAF测试 | MSAF测试 | 基区域 (逻辑门) | BDD面积 (逻辑门) |
|---|---|---|---|---|---|---|---|---|
| s298 | 3/6 | 17/20 | 114 | 70 | 48 | 48 | 75 | 121 |
| s382 | 3/6 | 24/27 | 213 | 167 | 64 | 191 | 99 | 170 |
| s400 | 3/6 | 24/27 | 213 | 167 | 67 | 191 | 106 | 170 |
| s526 | 3/6 | 24/27 | 195 | 144 | 79 | 128 | 141 | 198 |
| s27 | 4/1 | 7/4 | 22 | 18 | 11 | 9 | 8 | 20 |
| s444 | 4/6 | 25/27 | 220 | 167 | 75 | 190 | 119 | 175 |
| s386 | 7/7 | 13/13 | 198 | 51 | 51 | 114 | 118 | 144 |
| s1488 | 8/19 | 92/79 | 632 | 339 | 155 | 217 | 550 | 597 |
| s1494 | 8/19 | 14/25 | 632 | 283 | 153 | 215 | 558 | 594 |
| s344 | 9/11 | 24/26 | 135 | 249 | 49 | 276 | 101 | 178 |
| s208 | 11/2 | 19/10 | 76 | 30 | 53 | 68 | 66 | 80 |
| s1196 | 15/14 | 33/32 | 1149 | 1136 | 378 | 1906 | 388 | 1076 |
| s1238 | 15/14 | 33/32 | 1200 | 1136 | 382 | 1928 | 428 | 1103 |
| s953 | 16/23 | 45/52 | 653 | 235 | 165 | 331 | 311 | 543 |
| s420.1 | 18/1 | 34/17 | 206 | 169 | 114 | 252 | 140 | 193 |
| s820 | 18/19 | 23/24 | 377 | 127 | 107 | 195 | 256 | 312 |
| s510 | 19/7 | 25/13 | 229 | 110 | 85 | 85 | 179 | 246 |
| s1512 | 29/21 | 86/78 | 980 | 1948 | 446 | 17040 | 413 | 757 |
| s641 | 35/24 | 54/43 | 1157 | 925 | 421 | 1246 | 107 | 382 |
| s713 | 35/23 | 54/42 | 1130 | 912 | 387 | 1208 | 139 | 382 |
| s838 | 35/2 | 67/34 | 352 | 114 | 209 | 567 | 349 | 300 |
需要注意的是,综合是未优化的,以保持基于多路复用器的电路设计。表4的第7列和表5的第8列显示了基准电路的逻辑门数量。表4的第8列和表5的第9列显示了BDD实现后(根据gscl45nm库)的逻辑门数量。基于BDD的综合是非最小化的,因此在大多数情况下观察到门数量增加。 gscl45nm库中提供了2×1 mux作为单元,这使得许多电路在基于BDD综合后的门数量与原始门数量相当;例如clip, alu2, cmb。在某些情况下甚至更小;例如cm150a, tcon, cht。
需要注意的是,本文提出的测试方法仅适用于可由ROBDD表示的电路。对于路径数量非常多且生成 ROBDD日益困难的电路,本文的测试生成方法不再适用。
随着ROBDD节点深度的增加,路径长度随之增加,导致工作速度下降。未来可以研究一种将两级可测性综合与基于ROBDD的综合相结合的方法。这将有助于限制路径长度,并解决为大型电路构建二叉决策图的问题。
5 结论
在综合阶段之后,通过自动测试模式生成(ATPG)产生的单固定故障测试集可能无法覆盖逻辑电路中所有多固定型故障的组合。目前很少有综合方法能够为多 stuck-at 故障(MSAFs)提供良好的易于测试性。本文研究了一种基于简化有序二叉决策图(ROBDD)的综合方法,其中将 ROBDD的每个中间节点替换为一个 2×1 mux,以实现对 MSAFs的检测。首先,利用伪穷举测试和两级与或门( AND-OR gates)的MSAF检测原理,推导出一组可检测 2×1 mux内所有MSAFs的测试向量集。每个mux需要四个测试向量,即可充分检测该mux内部的所有MSAFs。进一步证明,当所有MSAF测试集合并后,能够检测整个电路的全部MSAFs。本文提出了两种用于MSAF检测的测试向量生成算法:一种基于BDD操作,另一种基于DSOP操作。由于设计和综合所对应的电路结构相同,因此可在设计阶段进行测试生成,从而消除了综合阶段后对ATPG的需求。尽管本研究中的MSAF可测性分析是针对基于多路复用器(mux)的电路开展的,但其同样适用于基于异或门的ROBDD实现。




















 671
671

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








