P1002 [NOIP 2002 普及组] 过河卒 c++题解

原创已于 2025-08-07 14:12:03 修改 · 2.1k 阅读

52 ·

CC 4.0 BY-SA版权

文章标签：

#c++ #代理模式 #开发语言

于 2025-08-06 21:21:22 首次发布

题解专栏收录该内容

5 篇文章

订阅专栏

P1002 [NOIP 2002 普及组] 过河卒 c++题解

题目链接

P1002 [NOIP 2002 普及组] 过河卒

题目描述

棋盘上 $A$ 点有一个过河卒，需要走到目标 $B$ 点。卒行走的规则：可以向下、或者向右。同时在棋盘上 $C$
点有一个对方的马，该马所在的点和所有跳跃一步可达的点称为对方马的控制点。因此称之为“马拦过河卒”。

棋盘用坐标表示， $A$ 点 $(0, 0)$ 、 $B$ 点 $(n, m)$ ，同样马的位置坐标是需要给出的。

现在要求你计算出卒从 $A$ 点能够到达 $B$ 点的路径的条数，假设马的位置是固定不动的，并不是卒走一步马走一步。

输入格式

一行四个正整数，分别表示 $B$ 点坐标和马的坐标。

输出格式

一个整数，表示所有的路径条数。

输入输出样例 #1

输入 #1

6 6 3 3

输出 #1

6

说明/提示

对于 $\%$ 的数据， $\le n, m \le 20$ ， $\le$ 马的坐标 $\le 20$ 。

【题目来源】

NOIP 2002 普及组第四题

1.题目内容

这道题目是NOIP2002普及组的经典动态规划问题，要求计算棋盘上卒从起点A(0,0)到终点B(n,m)的合法路径数，需避开马的控制点

2.难度

普及−

3.题目所需知识点

动态规划 DP
深度优先搜索 DFS

4. 思路

解题方法列举

动态规划解法（标准解法）

定义dp[i][j]表示从起点(0,0)到(i,j)的路径数，状态转移方程为： dp[i][j] = dp[i-1][j] + dp[i][j-1] 需预先标记马的控制点（马的位置及其8个跳跃点）为不可达区域。

记忆化搜索解法（递归思路‌）

从终点(n,m)反向递归，记录已计算子问题的结果。

注：需配合剪枝和记忆化数组

数学组合数解法（特殊场景）

当马的控制点不影响主要路径时，可用组合数公式：
C(n+m, n)

表示从(0,0)到(n,m)的总路径数。

‌限制‌ 需额外处理被马阻挡的路径，实际应用较少。

广度优先搜索（BFS）变种

队列存储待处理坐标。
从起点出发扩展右/下节点。
累计到达终点的路径数。

关键注意事项

必须使用long long，20x20棋盘路径数可达10级别。

‌边界处理‌

马的控制点需检查数组越界。

起点/终点重合需特判。

‌三种方法对比：

动态规划解法：
‌优势‌：
空间效率高‌：仅需二维数组存储状态（约0.5MB）。
‌边界处理简单‌：通过坐标偏移避免越界（整体+2）。
‌局限‌：
需严格处理马控点标记逻辑。

记忆化搜索： ‌
优势‌：
逻辑直观‌：符合路径搜索的自然思维 ‌。
自动剪枝‌：遇到马控点立即终止递归。
局限‌：
‌栈溢出风险‌：n=m=20时递归深度达40层，可能超限效率较低‌：递归调用开销比DP高5倍以上。

广度优先搜索：
‌优势‌： ‌
路径追踪能力‌：天然支持记录完整路径 ‌。
易处理动态障碍‌：适合马移动的变种问题。
局限‌：
空间爆炸‌：队列可能存储O(2ⁿ)级节点（n=20时超百万）。
时间效率最低‌：实测n=m=15即可能超时。

组合数学解法：
‌优势‌：
理论最快‌：无循环计算，O(1)时间复杂度。
学术价值高‌：展示动态规划与组合数学的关联。
局限‌：
实现复杂‌：需容斥原理排除多障碍点路径。
实用性低‌：马控点破坏路径连续性，公式难以修正。

故本题为动态规划解法讲解。其他提供代码，不做过多讲解

5.复杂度分析

时间复杂度

方法	时间复杂度	计算量示例 (n=m=20)	计算过程说明
‌动态规划‌	O(n×m)	400次	双层循环遍历整个棋盘
‌记忆化搜索‌	O(n×m)	400~800次	每个状态计算一次，但有递归开销
BFS‌	O(2^(n+m))	≈ 2⁴⁰ ≈ 10¹²次	最坏情况需遍历所有可能路径
‌组合数学‌	O(k²)或O(1)理论	9²=81次 (k为障碍数)	容斥原理处理障碍点

空间复杂度

方法	空间复杂度	内存消耗示例 (n=m=20)	主要存储结构
‌动态规划‌	O(n×m)	400个long long (3KB)	dp二维数组
‌记忆化搜索‌	O(n×m)+O(n+m)	400单元+调用栈40层	memo数组+递归栈
‌BFS‌	O(2^(n/2))	≈ 2²⁰ ≈ 100万节点	队列存储节点
‌组合数学‌	O(1)或O(k)	9个点坐标 (144字节)	障碍点坐标集合

6.动态规划解法详解

问题分析

目标‌：计算卒从起点 (0,0) 到达终点 (n,m) 的路径条数。
移动规则‌：卒只能‌向下或向右‌移动。‌
障碍点‌：对方的马所在位置及其跳跃可达的 8 个控制点（共 9 个点），卒不能经过这些点。‌
关键‌：使用动态规划（DP）记录到达每个点的路径数，避开障碍点。

动态规划步骤

1.标记马的控制点‌

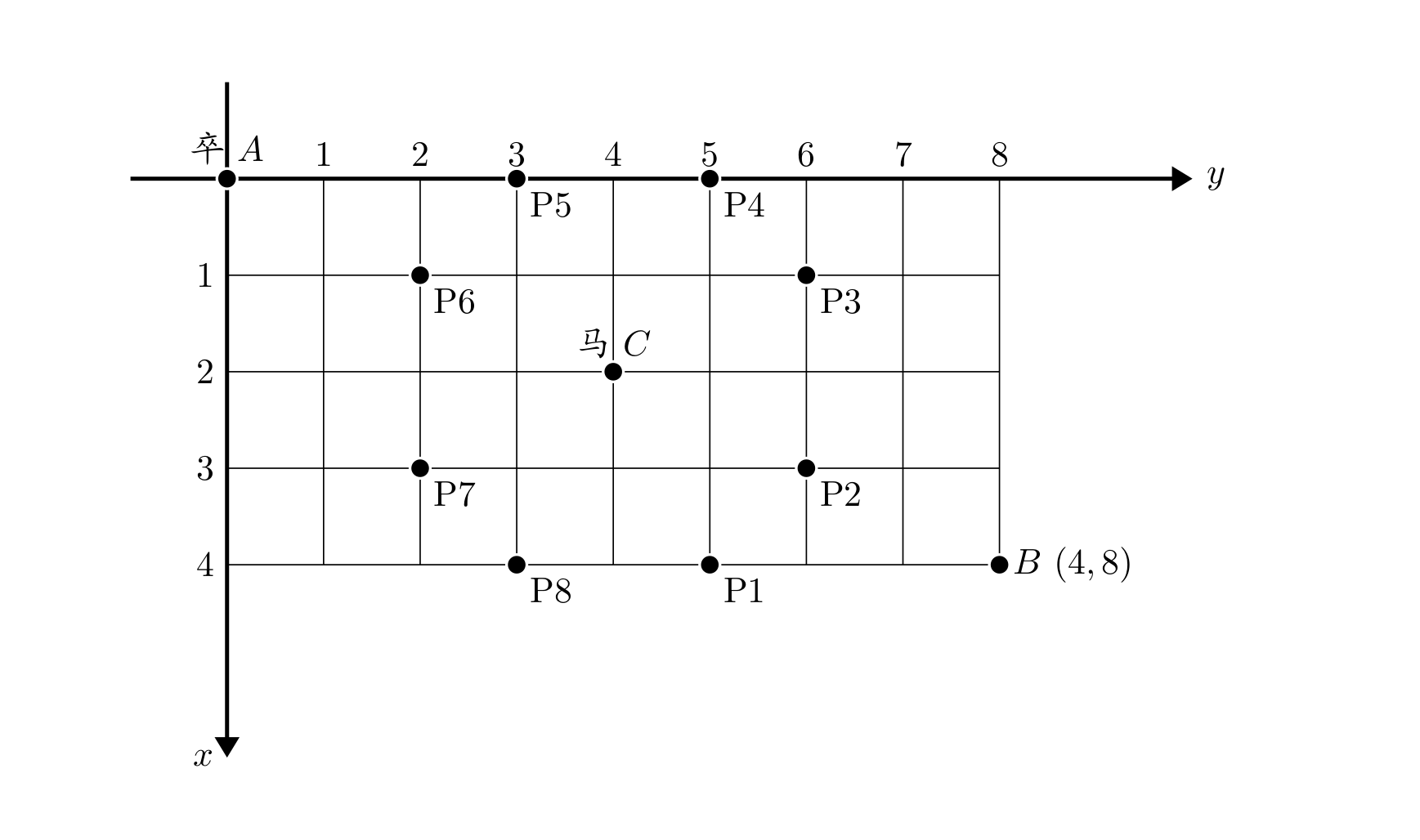
给定马的位置 (x,y)，计算其 8 个控制点（马走“日”字）：
(x-2, y-1), (x-2, y+1),
(x-1, y-2), (x-1, y+2),
(x+1, y-2), (x+1, y+2),
(x+2, y-1), (x+2, y+1)
‌包括马自身位置 (x,y)‌。

即下图中标红区域不能走
在这里插入图片描述

使用布尔数组 is_obstacle[i][j] 标记所有控制点（若坐标在 [0,n]×[0,m] 范围内）。
‌DP 状态定义‌
定义 dp[i][j]：从 (0,0) 到达 (i,j) 的路径条数。

2.边界初始化‌

起点 (0,0)‌：
- 若 (0,0) 是障碍点，则 dp[0][0] = 0（无路径）。
- 否则 dp[0][0] = 1。
第一行 (i=0, j>0)‌：
- 只能从左侧向右移动：
- dp[0][j] = dp[0][j-1]（若 (0,j) 无障碍）。
若遇到障碍点，则 dp[0][j] = 0，且后续点均为 0（无法到达）。
第一列 (j=0, i>0)‌：
- 只能从上方向下移动：
- dp[i][0] = dp[i-1][0]（若 (i,0) 无障碍）。
- 若遇到障碍点，则 dp[i][0] = 0，后续点为 0。

3.状态转移方程‌

对于非边界点 (i > 0, j > 0)：
- 若 (i,j) 是障碍点，则 dp[i][j] = 0。
- 否则，路径来自上方或左侧：
  dp[i][j] = dp[i-1][j] + dp[i][j-1]。

‌
4.遍历顺序‌

按行遍历（从左到右，从上到下）：
- 根据边界或转移方程计算 dp[i][j]

注意‌：计算 dp[i][j] 前需确保 dp[i-1][j] 和 dp[i][j-1] 已计算。

5‌.输出结果‌

最终答案：dp[n][m]（终点路径数）。

7.代码片段分析

初始化棋盘和dp数组（long long防溢出）

 long long dp[21][21]={0};
    bool danger[21][21]={false};

定义马的控制点偏移量（8个方向+马自身）

    int dir[9][2]={{1,2},{1,-2},{-1,2},{-1,-2},
                  {2,1},{2,-1},{-2,1},{-2,-1},
                  {0,0}}; // 最后一个是马本身

标记所有危险点（马的控制点）

 for (int i=0; i<9; i++){   //遍历9个方向（马自身位置+8个控制点）
        int nx=x+dir[i][0];      //dir[i][0]和dir[i][1]存储方向偏移量
        int ny=y+dir[i][1];
        if (nx>=0 && nx<=n && ny>=0 && ny<=m){     //边界检查
            danger[nx][ny]=true;
        }
    }

初始化起点(0,0)

 if (danger[0][0]){
    dp[0][0] = 0;  // 如果起点是危险点，则路径数为0
} 
   else{
    dp[0][0] = 1;  // 否则起点路径数为1（唯一初始路径）
}

动态规划填表

for (int i=0; i<=n; i++){
    for (int j=0; j<=m; j++){
        if (danger[i][j]) continue; // 跳过危险点
        
        // 如果不是第一行，累加上方路径数
        if (i>0) dp[i][j]+=dp[i-1][j];
        
        // 如果不是第一列，累加左侧路径数
        if (j>0) dp[i][j]+=dp[i][j-1];
    }
}

输出终点的路径总数

cout<<dp[n][m];

其他解法

1. 记忆化搜索（递归+缓存）

#include <iostream>
#include <cstring>
using namespace std;

// 马的控制点坐标偏移量（8个方向）
const int dx[] = {-2, -1, 1, 2, 2, 1, -1, -2};
const int dy[] = {1, 2, 2, 1, -1, -2, -2, -1};

long long dp[25][25]; // 记忆化数组
bool danger[25][25];  // 标记危险点

long long dfs(int x, int y, int n, int m) {
    // 越界或危险点返回0
    if (x > n || y > m || danger[x][y]) return 0;
    // 到达终点返回1
    if (x == n && y == m) return 1;
    // 已计算过直接返回
    if (dp[x][y] != -1) return dp[x][y];
    // 递归计算向右和向下的路径和
    return dp[x][y] = dfs(x + 1, y, n, m) + dfs(x, y + 1, n, m);
}

int main() {
    int n, m, x, y;
    cin >> n >> m >> x >> y;
    memset(dp, -1, sizeof(dp));
    // 标记马的控制点
    danger[x][y] = true;
    for (int i = 0; i < 8; i++) {
        int nx = x + dx[i], ny = y + dy[i];
        if (nx >= 0 && ny >= 0) danger[nx][ny] = true;
    }
    cout << dfs(0, 0, n, m);
    return 0;
}

2. 广度优先搜索（BFS）

#include<iostream>
#include <queue>
using namespace std;

const int dx[] = {-2, -1, 1, 2, 2, 1, -1, -2};
const int dy[] = {1, 2, 2, 1, -1, -2, -2, -1};

struct Node { int x, y; };

int main() {
    int n, m, x, y;
    cin >> n >> m >> x >> y;
    bool danger[25][25] = {false};
    long long cnt[25][25] = {0};
    
    // 标记马的控制点
    danger[x][y] = true;
    for (int i = 0; i < 8; i++) {
        int nx = x + dx[i], ny = y + dy[i];
        if (nx >= 0 && ny >= 0) danger[nx][ny] = true;
    }
    
    queue<Node> q;
    if (!danger[0][0]) {
        q.push({0, 0});
        cnt[0][0] = 1;
    }
    
    while (!q.empty()) {
        Node cur = q.front(); q.pop();
        // 向右移动
        if (cur.x + 1 <= n && !danger[cur.x + 1][cur.y]) {
            if (cnt[cur.x + 1][cur.y] == 0) q.push({cur.x + 1, cur.y});
            cnt[cur.x + 1][cur.y] += cnt[cur.x][cur.y];
        }
        // 向下移动
        if (cur.y + 1 <= m && !danger[cur.x][cur.y + 1]) {
            if (cnt[cur.x][cur.y + 1] == 0) q.push({cur.x, cur.y + 1});
            cnt[cur.x][cur.y + 1] += cnt[cur.x][cur.y];
        }
    }
    cout << cnt[n][m];
    return 0;
}

3.组合数学解法

#include <iostream>
#include <vector>
using namespace std;

// 马的控制点坐标偏移量（8个方向）
const int dx[] = {-2, -1, 1, 2, 2, 1, -1, -2};
const int dy[] = {1, 2, 2, 1, -1, -2, -2, -1};

// 计算组合数C(a,b) = a! / (b! * (a-b)!)
long long comb(int a, int b) {
    if (b < 0 || b > a) return 0;
    b = min(b, a - b); // 利用对称性减少计算量
    long long res = 1;
    for (int i = 1; i <= b; i++) {
        res = res * (a - b + i) / i; // 逐项计算避免溢出
    }
    return res;
}

int main() {
    int n, m, x, y;
    cin >> n >> m >> x >> y;
    
    // 标记所有危险点（马的位置+控制点）
    vector<vector<bool> > danger(n + 1, vector<bool>(m + 1, false));
    danger[x][y] = true;
    for (int i = 0; i < 8; i++) {
        int nx = x + dx[i], ny = y + dy[i];
        if (nx >= 0 && nx <= n && ny >= 0 && ny <= m) {
            danger[nx][ny] = true;
        }
    }
    
    // 检查起点或终点是否被阻挡
    if (danger[0][0] || danger[n][m]) {
        cout << 0;
        return 0;
    }
    
    // 总路径数 = C(n+m, n)
    long long total = comb(n + m, n);
    
    // 减去经过危险点的路径数
    for (int i = 0; i <= n; i++) {
        for (int j = 0; j <= m; j++) {
            if (danger[i][j]) {
                // 从(0,0)到(i,j)的路径数 × 从(i,j)到(n,m)的路径数
                long long bad = comb(i + j, i) * comb(n - i + m - j, n - i);
                total -= bad;
            }
        }
    }
    cout << total;
    return 0;
}

8.AC代码

#include <bits/stdc++.h>
using namespace std;
int n, m, x, y;
int main(){
    // 输入棋盘大小(n,m)和马的位置(x,y)
    cin>>n >>m>>x>>y;
    
    // 定义马的控制点偏移量（8个方向+马自身）
    int dir[9][2]={{1,2},{1,-2},{-1,2},{-1,-2},
                  {2,1},{2,-1},{-2,1},{-2,-1},
                  {0,0}}; // 最后一个是马本身
    
    // 初始化棋盘和dp数组（long long防溢出）
    long long dp[21][21]={0};
    bool danger[21][21]={false};
    
    // 标记所有危险点（马的控制点）
    for (int i=0; i<9; i++){   //遍历9个方向（马自身位置+8个控制点）
        int nx=x+dir[i][0];      //dir[i][0]和dir[i][1]存储方向偏移量
        int ny=y+dir[i][1];
        if (nx>=0 && nx<=n && ny>=0 && ny<=m){     //边界检查
            danger[nx][ny]=true;
        }
    }
    
    // 初始化起点(0,0)
   if (danger[0][0]){
    dp[0][0] = 0;  // 如果起点是危险点，则路径数为0
} 
   else{
    dp[0][0] = 1;  // 否则起点路径数为1（唯一初始路径）
}  
    
    // 动态规划填表
    for (int i=0; i<=n; i++){
        for (int j=0; j<=m; j++){
            if (danger[i][j]) continue; // 跳过危险点
            
            // 如果不是第一行，累加上方路径数
            if (i>0) dp[i][j]+=dp[i-1][j];
            
            // 如果不是第一列，累加左侧路径数
            if (j>0) dp[i][j]+=dp[i][j-1];
        }
    }
    
    // 输出终点的路径总数
    cout<<dp[n][m];
    return 0;
}