算法学习 排序总结 链表 双指针

排序算法综合 

	时间	空间	稳定性
选择	N2	1	F
冒泡	N2	1	T
插入	N2	1	T
归并	NlogN	N	T
快排	NlogN	logN	F
堆排	NlogN	1	F

稳定且快选择归并，最低 时间NlogN，空间N；
只要求快选择快排，性能最好；
要求空间复杂度低选堆排。

常见坑：
1.归并的空间复杂度可降到O(1)但丧失稳定性优势 （归并排序 内部缓存法）
2.“原地归并”会使时间复杂度升到O(N2)
3.快排可以解决稳定性，但空间复杂度会升到O(N) (01 stable sort)
4.奇数偶数划分，且相对位置不变，变相要求快排实现稳定性，见问题3

 

stl

哈希表 Set(key) Map(key,value)  常数级别
        java: HashSet/Map  c++:UnOrderSet/Map
        基础类型key按值传，引用类型key按地址传
有序表 Set(key) Map(key,value) 通过key组织 logN级别
         java: TreeSet/Map  c++:OrderedSet/Map
        基础类型key按值传，引用类型key按地址传
        红黑树，AVL树，Size-Blance-tree，跳表

 

链表

单链表(next)、双链表(next,last)

重要工具：额外辅助数据结构（哈希表）、快慢指针

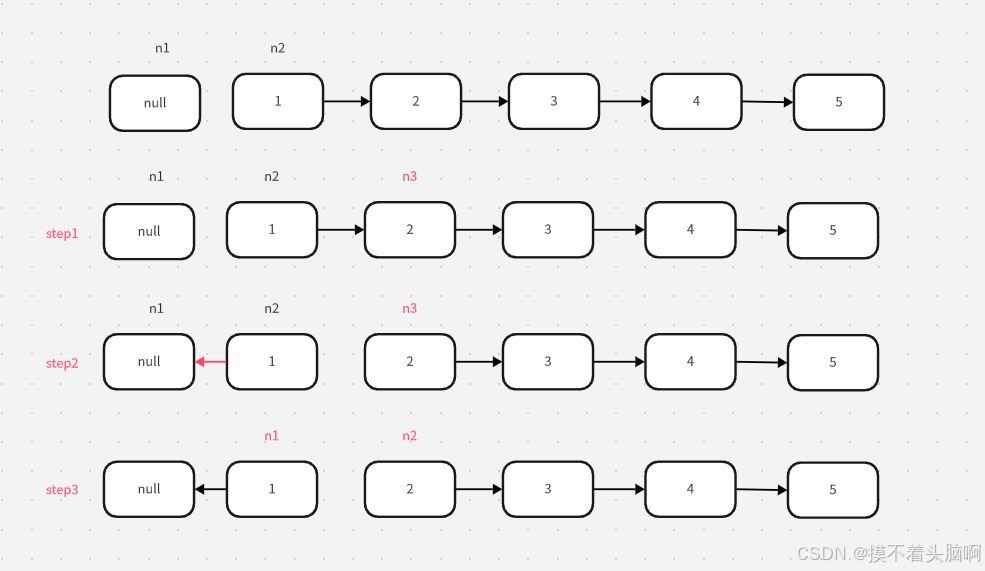
Q1:反转链表

while(n2!=null){
    n3=n2.next; //保存n2的next指针
    n2.next=n1; //修改n2next，指向前一个结点
    n1=n2; //后移
    n2=n3; //后移
}

Q2：打印两个有序链表的公共部分

双指针，较小节点往后移动，每次移动判断是否相同，直至任意指针指空。

 

Q3：回文字符串

法1：栈

法2：

快慢指针 (有时候需要微调) 注意边界条件，表长较短时

while(n2.next!=null&&n2.next.next!=null){
    n1=n1.next;
    n2=n2.next.next;
}

反转mid之后的链表 Q1

判断回文

恢复链表 Q1

 

Q4：链表的荷兰国旗问题，将链表划分为左小，中等，右大的形式

维护6个指针，左区域的头尾，中间区间的头尾，右区域的头尾，最后再首尾相接，相接时注意判断某区域是否为空。

 

Q5：复制含随机指针节点的链表Node(next,random)

法1：HashMap克隆（Node，Node0）根据原结点方便访问到克隆结点，再遍历连接next，random指针

法2：克隆结点放于原结点之后，即Node.next=Node0 ，修改完原链表后，遍历复制克隆结点的random指针，可通过Node.next=Node0寻找原结点和克隆结点的对应关系。最后分离修改后的链表，将Node和Node0分开。Node.next.next为原来的next结点。

Q6:两个单链表相交的一系列问题
给定两个可能有环的单链表，head1和head2，若两个链表相交，返回第一个相交结点，若不交，返回null

         子问题1：IsLoop( ) 判断是否有环，若有返回第一个入环结点

        法1：用Set
        法2：用快慢指针  慢1，快2
             1.无环的情况，快指针一定指空
             2.有环的情况，快慢指针在环相遇，慢入环后两圈内快必遇上快。相遇后快指针指头结点，慢指第一次相遇结点，慢1快1，下一相遇点即为第一个入环结点。
证明：设头结点到入环点距离为a，第一次相遇点离入环点的距离为x，环长为r
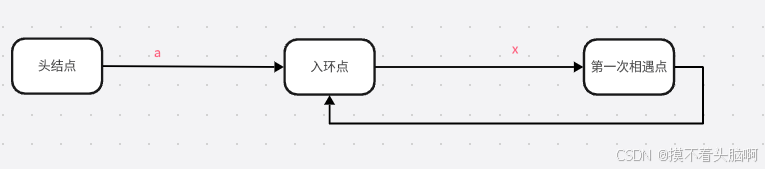假设相遇时快指针在环中走过n圈，慢指针走过m圈，则2（a+x+m*r）=a+x+n*r

a=(n-2m)*r-x
               

情况1：loop1==null，loop2==null
遍历两个链表，记录len1，end1，len2，end2。若end不相同则，不交，若end同，让len短的先走abs(len1-len2)，再一起走。

情况2：其中一个loop不为空，必不相交

情况3：loop都不为空

        1）loop相同，转情况1中end相同的情况。
        2）loop不同，分两种，第一种是不同环，第二种是同环。让其中一个loop继续走，再次遇到自己时没遇上另外一个loop，则为第一种情况无交点，否则为第二种情况其中一个loop为交点。