Transformer：核心架构多头注意力机制（Multi-Head Attention（MHA））

为了更清晰地展示 Transformer Encoder Block 中的数学运算，我们将以矩阵形式来表达每个步骤。假设输入是一个形状为 (L,d)(L,d) 的矩阵X，其中 L 是序列长度，d 是隐藏维度。

1. Multi-Head Attention（MHA）

输入：

• 

线性变换得到 Q, K, V：

其中：

• ​ 是权重矩阵，
• dk=d/h 是每个头的维度，h 是注意力头的数量。

Scaled Dot-Product Attention 计算：

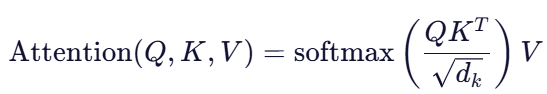
由于我们使用的是 Multi-Head Attention，所以需要对 Q,K,V 进行划分，并独立计算每个头的注意力输出。

每个头的注意力输出为：

将所有头的结果拼接并投影回原始维度：

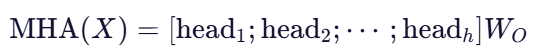
其中是用于投影的权重矩阵。

2. Add & Norm（残差连接 + 层归一化）

对于第一层的 Add & Norm：

3. Feed-Forward Network（FFN）

FFN 包含两个线性变换和一个激活函数（通常为 ReLU）：

矩阵形式表示为：

其中：

•  是权重矩阵，
•  是偏置项（在实际实现中，偏置项通常是按列广播的）。

4. 第二层的 Add & Norm

对于第二层的 Add & Norm：

5. 完整 Encoder Block 公式

综合以上步骤，整个 Encoder Block 可以表示为：

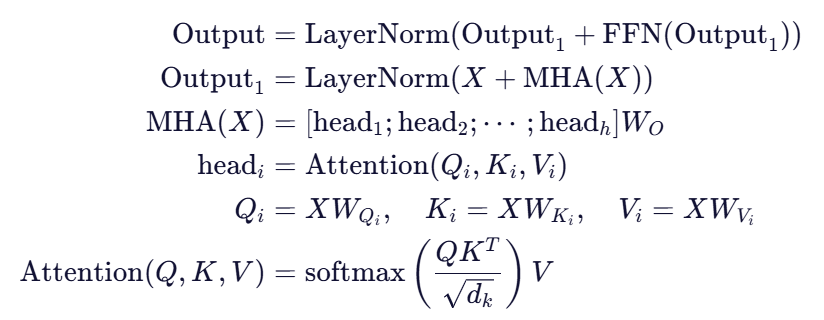
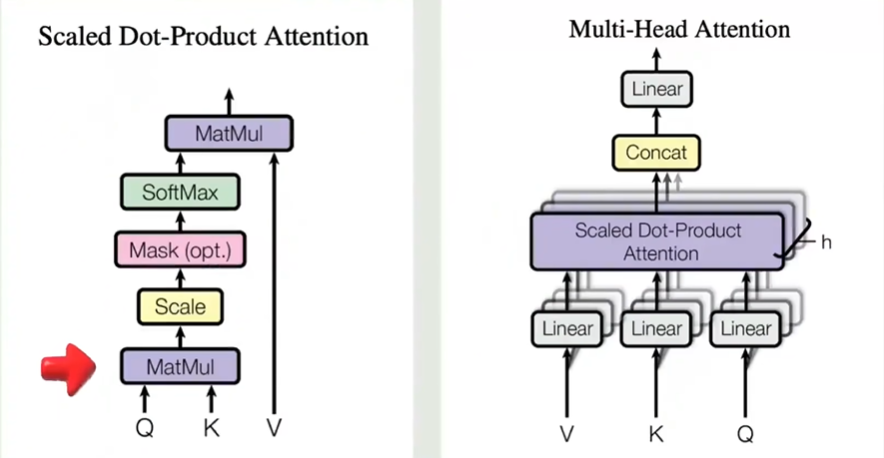
注意力机制：先是Q和K相乘得到一个相似系数的矩阵，然后再和V相乘最终得到一个包含上下文信息的词（向量矩阵）

多头注意力机制：V、K、Q分别经过线性变换，然后分组。每一组进行Scaled Dot-Product Attention 学习到不同的相似关系

经过注意力计算后将其Cnoncat拼接起来
 

---

示例：具体矩阵尺寸

假设：

• 序列长度 L=10
• 隐藏维度 d=512
• 注意力头数 h=8
• 每个头的维度 （因为 ）
• 前馈网络中间层维度

那么：

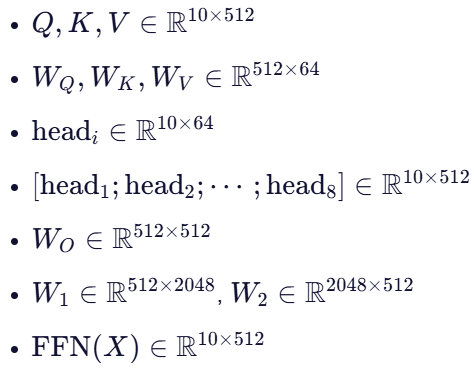
这样，通过这些矩阵运算，我们可以看到数据如何在 Transformer 的 Encoder Block 中流动和变换。