图神经网络进阶：用 PyTorch Geometric 实现标准 GCN 并分析其优势

最新推荐文章于 2025-11-23 19:49:42 发布

原创最新推荐文章于 2025-11-23 19:49:42 发布 · 2.3k 阅读

7 ·

CC 4.0 BY-SA版权

文章标签：

#神经网络 #pytorch #人工智能 #图网络

图网络专栏收录该内容

12 篇文章

订阅专栏

🔍 代码分段详解

🔹 第一部分：导入库与加载数据

import torch
from torch_geometric.datasets import Planetoid
from torch_geometric.utils import degree
from collections import Counter
import matplotlib.pyplot as plt
import torch.nn.functional as F
from torch_geometric.nn import GCNConv

Planetoid：加载 Cora、CiteSeer 等标准图数据集。
degree：计算每个节点的度（即邻居数量）。
Counter + matplotlib：用于统计并可视化节点度分布。
GCNConv：PyTorch Geometric 提供的标准图卷积层（已实现归一化）。

dataset = Planetoid(root="D:\\py机器学习\\data", name="Cora")
data = dataset[0]

加载 Cora 数据集（2708 个节点，每个节点是论文，特征为词袋向量，标签为 7 类主题）。
data 包含：x（特征）、y（标签）、edge_index（边）、train/val/test_mask。

🔹 第二部分：分析节点度分布（解释为何需要归一化）

degrees = degree(data.edge_index[0]).numpy()
numbers = Counter(degrees)

fig, ax = plt.subplots()
ax.set_xlabel('Node degree')
ax.set_ylabel('Number of nodes')
plt.bar(numbers.keys(), numbers.values())
plt.show()

✅ 作用：

统计图中每个节点的度（degree），即有多少条边连接到它。
绘制直方图，展示度分布是否均匀。

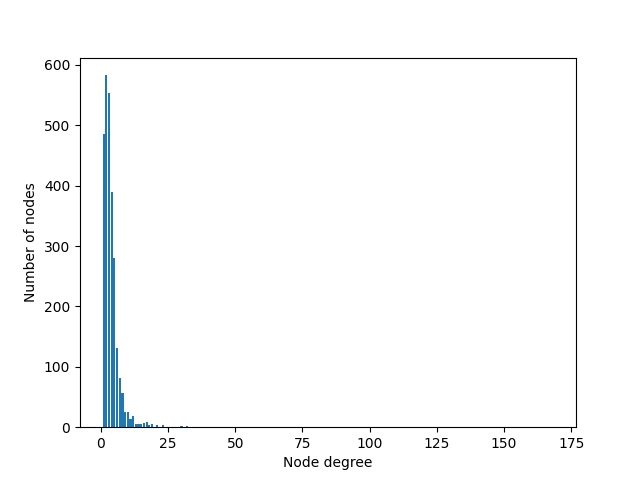
📌 为什么重要？

在朴素 GNN（如你之前的 VanillaGNN）中，聚合方式是简单求和：
$( h_i = \sum_{j \in \mathcal{N}(i)} x_j )$
如果某个节点有 100 个邻居，另一个只有 2 个，前者的聚合结果会数值过大，导致训练不稳定。
GCN 通过归一化解决此问题：
$( h_i = \sum_{j \in \mathcal{N}(i)} \frac{1}{\sqrt{d_i d_j}} x_j )$
（其中 ( d_i ) 是节点 i 的度）

✅ 这段可视化正是为后续使用 GCNConv 做铺垫：展示“度差异大 → 需要归一化”。

🔹 第三部分：定义准确率函数

def accuracy(y_pred, y_true):
    return torch.sum(y_pred == y_true) / len(y_true)

标准分类准确率计算，与之前一致。

🔹 第四部分：定义 GCN 模型

class GCN(torch.nn.Module):
    def __init__(self, dim_in, dim_h, dim_out):
        super().__init__()
        self.gcn1 = GCNConv(dim_in, dim_h)
        self.gcn2 = GCNConv(dim_h, dim_out)

    def forward(self, x, edge_index):
        h = self.gcn1(x, edge_index)
        h = torch.relu(h)
        h = self.gcn2(h, edge_index)
        return F.log_softmax(h, dim=1)

✅ 关键点：

使用 GCNConv，它内部已实现：
- 自环添加（自动处理）
- 对称归一化 $( \hat{D}^{-1/2} \hat{A} \hat{D}^{-1/2} X W )$
- 稀疏矩阵高效计算（无需转稠密）
输入是 x 和 edge_index（稀疏格式），不是邻接矩阵，更高效、更标准。
两层结构：1433 → 16 → 7，与之前模型一致，便于对比。

🔹 第五部分：训练方法（fit）

    def fit(self, data, epochs):
        criterion = torch.nn.NLLLoss()
        optimizer = torch.optim.Adam(self.parameters(), lr=0.01, weight_decay=5e-4)
        self.train()
        for epoch in range(epochs+1):
            optimizer.zero_grad()
            out = self(data.x, data.edge_index)  # ← 使用 edge_index！
            loss = criterion(out[data.train_mask], data.y[data.train_mask])
            acc = accuracy(out[data.train_mask].argmax(dim=1), data.y[data.train_mask])
            loss.backward()
            optimizer.step()

            if epoch % 20 == 0:
                val_loss = criterion(out[data.val_mask], data.y[data.val_mask])
                val_acc = accuracy(out[data.val_mask].argmax(dim=1), data.y[data.val_mask])
                print(f'Epoch {epoch:>3} | Train Loss: {loss:.3f} | ...')

标准训练循环，每 20 轮打印验证性能。
注意：没有手动处理邻接矩阵，GCNConv 自动处理图结构。

🔹 第六部分：测试方法（test）

    @torch.no_grad()
    def test(self, data):
        self.eval()
        out = self(data.x, data.edge_index)
        acc = accuracy(out.argmax(dim=1)[data.test_mask], data.y[data.test_mask])
        return acc

在测试集上评估，使用 test_mask。

🔹 第七部分：实例化、训练与测试

gcn = GCN(dataset.num_features, 16, dataset.num_classes)
print(gcn)

gcn.fit(data, epochs=100)
acc = gcn.test(data)
print(f'\nGCN test accuracy: {acc*100:.2f}%\n')

📊 输出解读：

Epoch   0 | Train Acc: 16.43% → 随机水平（7类，理论随机≈14.3%）
Epoch  20 | Train Acc: 100.00% → 训练集过拟合（常见于小图）
Val Acc: 77.20% → 验证集稳定在 77%+
Test Acc: 80.80% → **显著优于 MLP（~58%）和 VanillaGNN（~75%）**