实值复变函数的凹凸性判断

判断一个函数的凹凸性在很多问题中是非常重要的。当一个函数是凸（凹）的，那么与其相关的很多优化问题可以被简单地求解。

众所周知，对于自变量为实数值的函数，可以通过计算实值函数的Hessian矩阵来判断其凹凸性。然而，当自变量是复数值时，我们甚至找不到一个统一的Hessian矩阵定义方式。那么，如何判断实值复变函数的凹凸性呢？

首先，我们来看对于实值复变函数的导数的定义。由于实值复变函数往往包含共轭或共轭转置，这就意外着这些函数很多时候是不解析的，也就是不满足柯西-黎曼条件。因此，在实值复变函数的研究中，往往采用Wirtinger导数，其定义为：

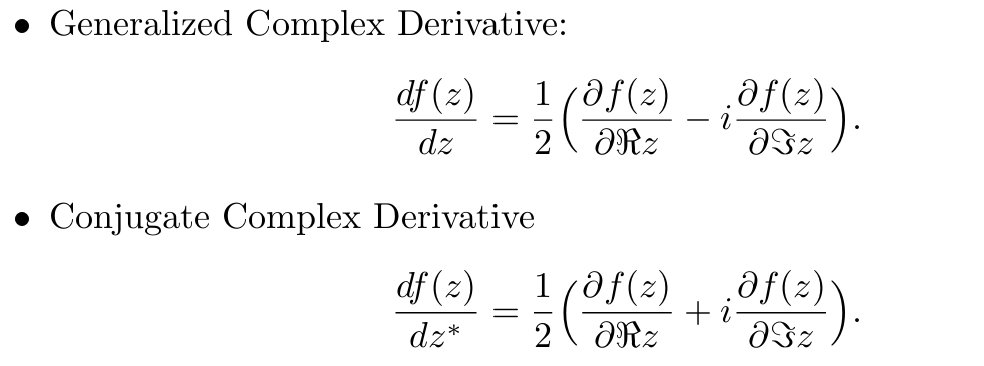
其中*代表一个数的共轭。可以看到，在Wirtinger导数中，我们认为自变量z与它的共轭是独立的。从f对z的共轭的导数我们也可以知道，f对于z的Wirtinger梯度可以被定义为

这便是函数随着自变量变化最快的方向。上述内容见Kaare Brandt Petersen等人的The Matrix Cookbook的Section 4。

那么，Hessian矩阵又该如何定义呢？在这里，我们采用Ali H. Sayed的Adaptation, learning, and optimization over networks中的定义：

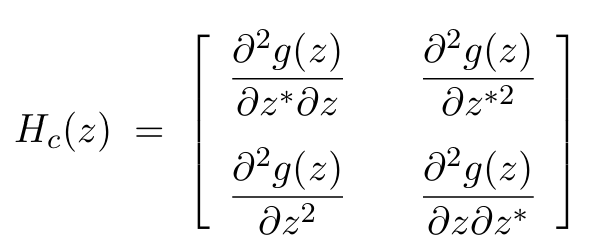
当自变量是2×1的向量时：

可以看到，对于自变量为M维向量的实值复变函数，Hessian矩阵变成了2M×2M的矩阵，其正定性可用于判断函数的凹凸性（见Adaptation, learning, and optimization over networks的Appendix B.2.2）

你可能会想，这样一个形状的Hessian矩阵，又该如何用于Taylor展开呢？事实上，当你考虑自变量是复数的时候，由于函数往往不解析，这就意味着它不能展开（Weierstrass定理），如果你非要展开，我的个人建议是首先将其看做实值函数，展开后再考虑怎么变为复变的形式（见祁忠勇等人的Convex Optimization for Signal Processing and Communications: From Fundamentals to Applications的Section 4.3.5）。

实际上，复变函数的Hessian矩阵还有很多定义，如  A. van den Bos等人的文章Complex Gradient and Hessian中的定义：

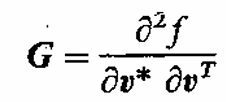
其中

。

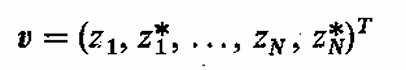个人研究体悟，如有错误，敬请指正。