Leetcode32.最长有效括号

Leetcode32.最长有效括号

题目：
给你一个只包含 ‘(’ 和 ‘)’ 的字符串，找出最长有效（格式正确且连续）括号子串的长度。

示例 1：

输入：s = "(()"
输出：2
解释：最长有效括号子串是 "()"

示例 2：

输入：s = ")()())"
输出：4
解释：最长有效括号子串是 "()()"

示例 3：

输入：s = ""
输出：0

方案一：
动态规划：
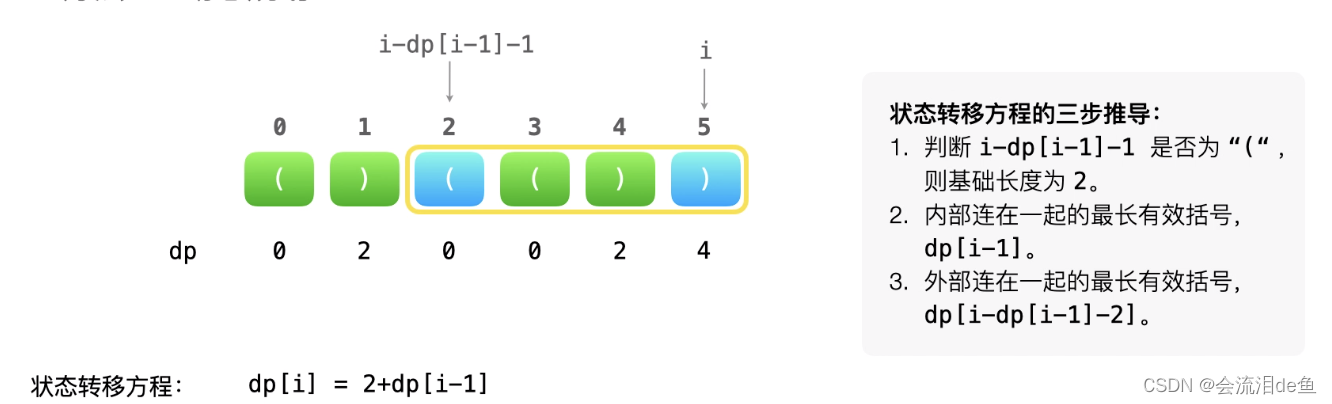
我们定义 $dp[i]$ 表示以下标 ii 字符结尾的最长有效括号的长度。我们将 $dp$ 数组全部初始化为 $0$ 。显然有效的子串一定以‘)’ 结尾，因此我们可以知道以 ‘(’ 结尾的子串对应的 $dp$ 值必定为 0 ，我们只需要求解 ‘)’ 在 dp 数组中对应位置的值。

方案二：
使用额外空间栈

  具体做法是我们始终保持栈底元素为当前已经遍历过的元素中「最后一个没有被匹配的右括号的下标」，这样的做法主要是考虑了边界条件的处理，栈里其他元素维护左括号的下标：

• 对于遇到的每个 ‘(’ ，我们将它的下标放入栈中

• 对于遇到的每个 ‘)’ ，我们先弹出栈顶元素表示匹配了当前右括号：

  • 如果栈为空，说明当前的右括号为没有被匹配的右括号，我们将其下标放入栈中来更新我们之前提到的「最后一个没有被匹配的右括号的下标」
  • 如果栈不为空，当前右括号的下标减去栈顶元素即为「以该右括号为结尾的最长有效括号的长度」
    我们从前往后遍历字符串并更新答案即可。

需要注意的是，如果一开始栈为空，第一个字符为左括号的时候我们会将其放入栈中，这样就不满足提及的「最后一个没有被匹配的右括号的下标」，为了保持统一，我们在一开始的时候往栈中放入一个值为 -1的元素。

java代码：

/**
     * 动态规划：dp[i] = 2 + dp[i - 1] + dp[i - dp[i - 1] - 2]
     *
     * @param s
     * @return
     */
    public static int longestValidParentheses(String s) {
        int len = s.length();
        int max = 0;
        int[] dp = new int[len];

        for (int i = 1; i < len; i++) {
            //i - dp[i - 1] - 1是与当前')'对应的位置
            if (s.charAt(i) == ')' && i - dp[i - 1] - 1 >= 0 && s.charAt(i - dp[i - 1] - 1) == '(') {
                dp[i] = 2 + dp[i - 1] + (i - dp[i - 1] - 2 >= 0 ? dp[i - dp[i - 1] - 2] : 0);
            }
            max = Math.max(max, dp[i]);
        }
        return max;
    }


    /**
     * 使用额外空间栈
     *
     * @param s
     * @return
     */
    public static int longestValidParentheses1(String s) {
        int max = 0;
        Deque<Integer> stack = new LinkedList<>();
        stack.push(-1);
        for (int i = 0; i < s.length(); i++) {
            if (s.charAt(i) == '(') {
                stack.push(i);
            } else {
                stack.pop();
                if (stack.isEmpty()) {
                    stack.push(i);
                } else {
                    max = Math.max(max, i - stack.peek());
                }
            }
        }
        return max;
    }