Leetcode62. 不同路径
题目:
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为“Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为“Finish”)。
问总共有多少条不同的路径?
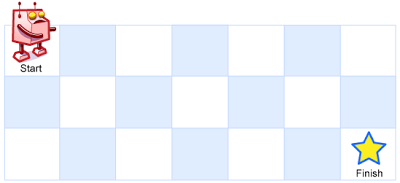
例如,上图是一个7 x 3 的网格。有多少可能的路径?
示例 1:
输入: m = 3, n = 2
输出: 3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
- 向右 -> 向右 -> 向下
- 向右 -> 向下 -> 向右
- 向下 -> 向右 -> 向右
示例 2:
输入: m = 7, n = 3
输出: 28
题解:
-
方案一:动态规划
我们令 dp[i][j]dp[i][j]dp[i][j] 是到达 i, j 最多路径
动态方程:dp[i][j]=dp[i−1][j]+dp[i][j−1]dp[i][j] = dp[i-1][j] + dp[i][j-1]dp[i][j]=dp[i−1][j]+dp[i][j−1] -
方案二:优化
我们在二维数组推导的时发现,dp[i][j]dp[i][j]dp[i][j]的值来自于dp[i−1][j]dp[i - 1][j]dp[i−1][j]和dp[i][j−1]dp[i][j - 1]dp[i][j−1]。
也就是只需要上一行的值就可以了,上上一行的并不需要了,所以这里可以用滚动数组的方式优化一下空间。
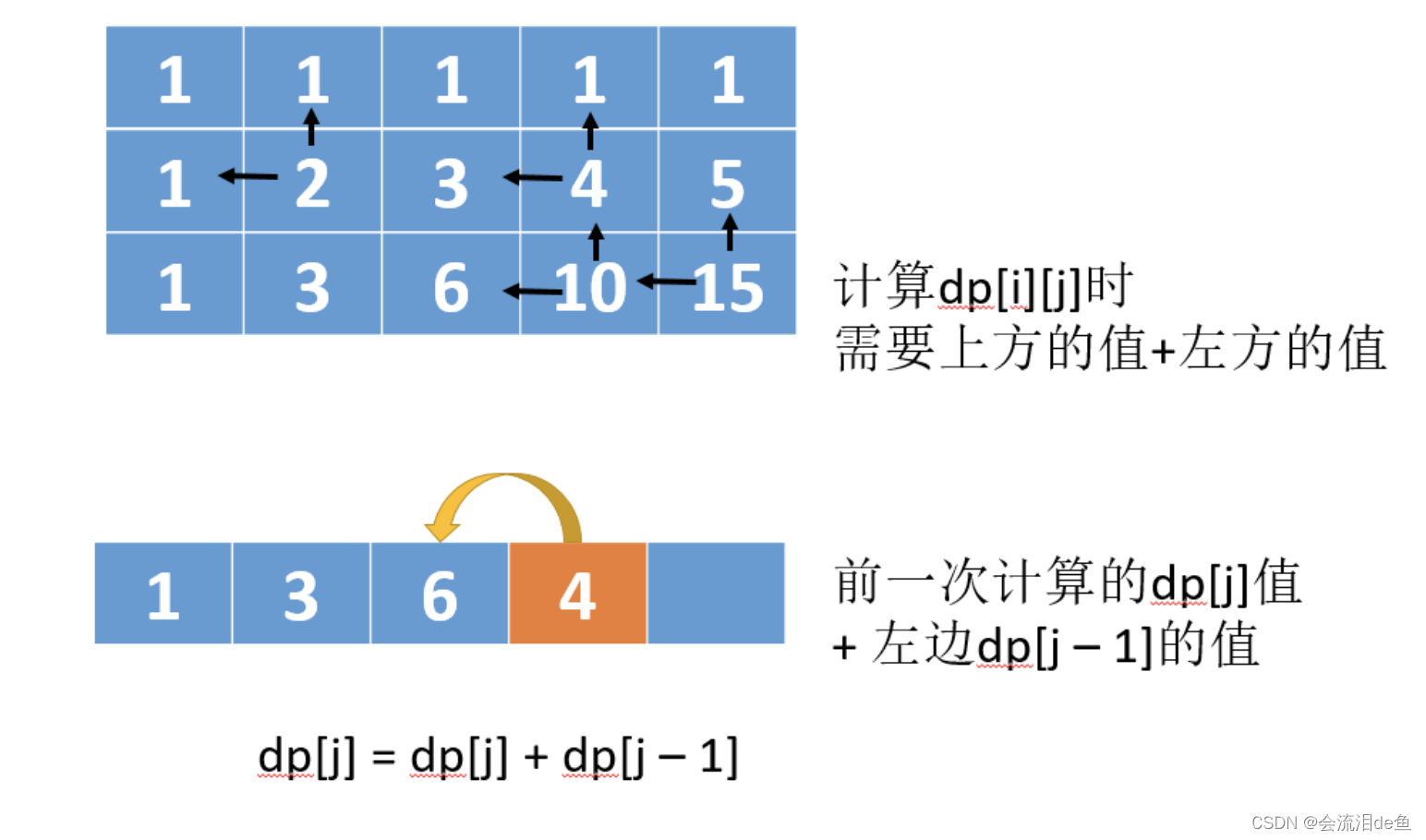
动态方程:dp[j]=dp[j]+dp[j−1]dp[j] = dp[j] + dp[j - 1]dp[j]=dp[j]+dp[j−1]
java代码:
/**
* dp[i][j]=dp[i][j-1]+dp[i-1][j]
*
* @param m
* @param n
* @return
*/
public static int uniquePaths(int m, int n) {
int[][] dp = new int[m][n];
for (int i = 0; i < m; i++) dp[i][0] = 1;
for (int j = 0; j < n; j++) dp[0][j] = 1;
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = dp[i][j - 1] + dp[i - 1][j];
}
}
return dp[m - 1][n - 1];
}
/**
* 只保留当前行信息
* dp[j] = dp[j] + dp[j - 1]
*
* @param m
* @param n
* @return
*/
public static int uniquePaths2(int m, int n) {
int[] dp = new int[n];
dp[0] = 1;
for (int i = 0; i < m; i++) {
for (int j = 1; j < n; j++) {
//等式右边的 dp[j]是上一次计算后的,加上左边的dp[j-1]即为当前结果
dp[j] = dp[j] + dp[j - 1];
}
}
return dp[n - 1];
}





 本文详细解析了LeetCode 62题“不同路径”的解决方案,通过动态规划方法求解机器人从网格左上角到右下角的不同路径数量。文章介绍了两种方法:一是传统的二维动态规划;二是优化的空间复杂度,使用滚动数组减少内存消耗。
本文详细解析了LeetCode 62题“不同路径”的解决方案,通过动态规划方法求解机器人从网格左上角到右下角的不同路径数量。文章介绍了两种方法:一是传统的二维动态规划;二是优化的空间复杂度,使用滚动数组减少内存消耗。

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








