Leetcode121. 买卖股票的最佳时机

Leetcode121. 买卖股票的最佳时机

题目：
给定一个数组，它的第 i 个元素是一支给定股票第 i 天的价格。
如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。
注意你不能在买入股票前卖出股票。
例 :
输入: [7,1,5,3,6,4]
输出: 5
解释: 在第 2 天（股票价格 = 1）的时候买入，在第 5 天（股票价格 = 6）的时候卖出，最大利润 = 6-1 = 5 。
注意利润不能是 7-1 = 6, 因为卖出价格需要大于买入价格。
题解：
暴力法：
时间复杂度：$O(n^2)$。循环运行$\frac{n(n-1)}{2}$ 次。
空间复杂度：$O(1)$。只使用了两个变量 —— $\text{maxprofit}$和 $\text{profit}$。
一次遍历：

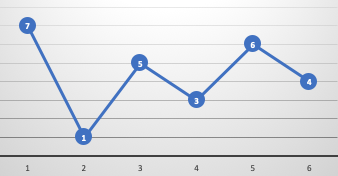
我们需要找到最小的谷之后的最大的峰。
我们可以维持两个变量——minprice 和 maxprofit，它们分别对应迄今为止所得到的最小的谷值和最大的利润（卖出价格与最低价格之间的最大差值）。
时间复杂度：O(n)，只需要遍历一次。
空间复杂度：O(1)，只使用了两个变量。
scala代码如下：
暴力法：

def maxProfit(prices: Array[Int]): Int = {
    var maxprofit = 0
    for (i <- 0 until prices.length) {
      for (j <- i until prices.length) {
        val profit = prices(j) - prices(i)
        if (profit > maxprofit) {
          maxprofit = profit
        }
      }
    }
    maxprofit
  }

一次遍历：

 def maxProfit2(prices: Array[Int]): Int = {
    var min = Int.MaxValue
    var maxprofit = 0
    for (i <- 0 until prices.length) {
      if (prices(i) < min) {
        min = prices(i)
      } else if (prices(i) - min > maxprofit) {
        maxprofit = prices(i) - min
      }
    }
    maxprofit
  }