[图] 医院选址问题 - 最短路径Floyd应用 - C语言实现

【问题背景】

已知有向图的邻接矩阵如下图所示，需在其中一个结点建立医院
	要求：
		1. 该结点距其他各个结点的最长往返路径最短
		2. 相同条件下总的往返路程越短越好
	矩阵：
		0	13	∞	4	∞
		13	0	15	∞	5
		∞	∞	0	12	∞
		4	∞	12	0	∞
		∞	∞	6	3	0

【思路】

最长往返路径
		1. 该矩阵是一个有向图，也就是说A->B的路径，可能并不是B->A的路径
		2. 最长往返路径= A->B的路径长度 + B->A的路径长度
	思路：最短路径的应用问题
		1. 求出任意两点之间的最短路径长度
		2. 遍历每一个结点，计算该结点到其余结点的最长往返路径max，总的SUM
		3. 取出max最小的，即为医院的地址
			其中，max相同的话，看sum，sum最小的为医院的地址
	使用算法：
		常用的最短路径算法有Dijkstra与Floyd
		1. Dijkstra常用与一个结点到其余各点的最短路径的情景
		2. Floyd常用与求任意两点的最短路径
		这里我们选Floyd更方便

【结果】

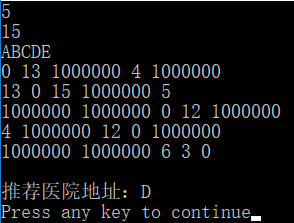
【代码】

#