②DFS深度优先搜索（基础）

1.介绍        

        深度优先搜索属于图算法的一种，英文缩写为DFS即Depth First Search.其过程简要来说是对每一个可能的分支路径深入到不能再深入为止，而且每个节点只能访问一次。

2.图例

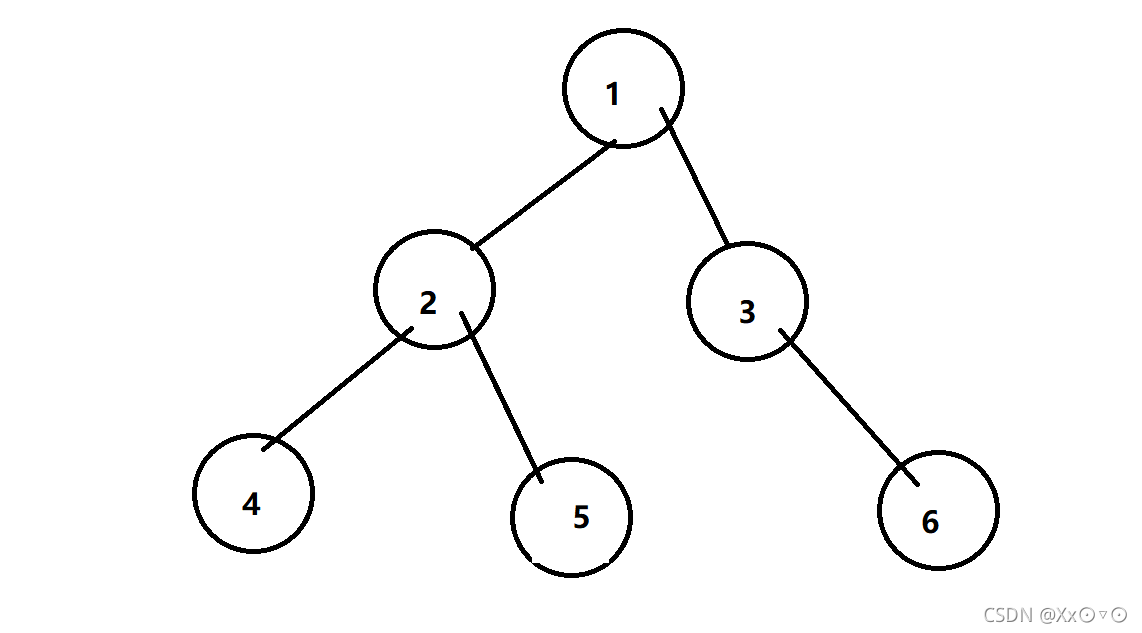
        对于这样一个图来说，假设起点为1，则深度优先遍历的遍历结果为1->2->4->5->3->6

解释

因为DFS搜索是对每一个分支路径深入到不能深入为止

所以第一步:从1->2->4，然后到了叶子节点，不能再深入了。

第二步：节点4回溯到节点2。

第三步：节点2发现还有节点5没有遍历到，于是深入到节点5。

第四步：节点5发现自己是叶子节点，没有办法深入了，于是回溯到节点2。

第五步：节点2发现节点4和节点5都已经遍历过了，于是自己的任务完成了，于是回溯到根节点1。

第六步：根节点1发现自己的儿子节点还有节点3没有遍历，于是深入到节点3。

第七步：节点3发现自己还能深入到节点6，于是深入到节点6。

第八步：节点6发现自己是叶子节点，已经没办法深入了，于是回溯到节点3，节点3回溯到节点1，节点1发现自己的左子树和右子树都访问过了，于是dfs结束。

对于这样的过程，代码如下：

输入：

1 2
1 3
2 4
2 5
3 6
0

输出：

1 2 4 5 3 6

#include<iostream>
using namespace std;

const int maxn = 7;
bool g[maxn][maxn];//邻接矩阵
bool vis[maxn];//判断是否访问过

void dfs(int start) {//输入起点
	vis[start] = true;
	cout << start << " ";
	for (int i = 1; i < maxn; i++)
		if (g[start][i] && !vis[i])dfs(i);
}

int main() {
	ios::sync_with_stdio(false), cin.tie(0);
	int s, e;//起点与终点
	while (true) {
		cin >> s;
		if (s == 0)break;//如果起点为0则结束读入
		cin >> e;
		g[s][e] = g[e][s] = true;
	}
	dfs(1);
	return 0;
}