【基础算法】堆排序与TopK问题（C语言）

目录

堆：

完全二叉树的数组实现：

堆的实现：

向下调整：

堆排序：

 TopK问题：

力扣面试题举例：

 建堆：

---

堆：

堆(Heap)是一类特殊的数据结构，是最高效的优先级队列。堆通常是一个可以被看作一棵完全二叉树的数组对象。堆分大堆和小堆，大堆的每个父亲都比孩子要大，小堆的每个父亲都比孩子要小。建议大家了解二叉树后再来学习堆排序。

完全二叉树的数组实现：

给定一个数组

int arr[10]={1,2,3,4,5,6,7,8,9,10};

这是数组的物理存储方式，那怎么样才能把逻辑存储方式转换为二叉树呢？

如图，1的孩子有2和3 ，2的孩子有4和5，我们想通过1来访问到2和3，想通过2来访问到4和5，只需要通过公式（parent为当前节点下标,child_left和child_right为当前节点的两个孩子的下标）

child_left=parent*2+1      child_right=parent*2+2

即该节点的左孩子和该节点的右孩子

我们来通过上面的公式试试

可以看到通过上面的式子就可以找到该节点的左孩子和右孩子的下标

那怎么通过孩子的下标来找到父亲的下标呢？其实就是把上面的公式反过来

parent=(child-1)/2(因为(6-1)/2和(5-1)/2相同(左孩子是奇数，右孩子是偶数))

堆的实现：

向下调整：

这里就以小堆来演示，小堆是指每个节点的值都比它的孩子的值要小

在一棵二叉树的两个子树都已经是小（大）堆的条件下，就可以通过“向下调整”来让整棵树变成小（大）堆

比如这个二叉树

int arr[10]={6,1,3,4,6,5,7,7,9,10};

 我们可以看到这棵树除了根节点，它的两个子树都已经是小堆，这时就可以用上面提到的“向下调整”来让整颗树都变成小堆

具体做法就是让根节点和他的两个孩子比较，把如果两个孩子中有比根节点还要小的，就交换。

这时再把与根交换的这个孩子看做父亲，继续与它的两个孩子比较，直到父亲比两个孩子都小或者到末尾为止。

图解：(红框为当前子树的根，也就是需要向下调整的节点，粉色为与红色节点交换的节点)

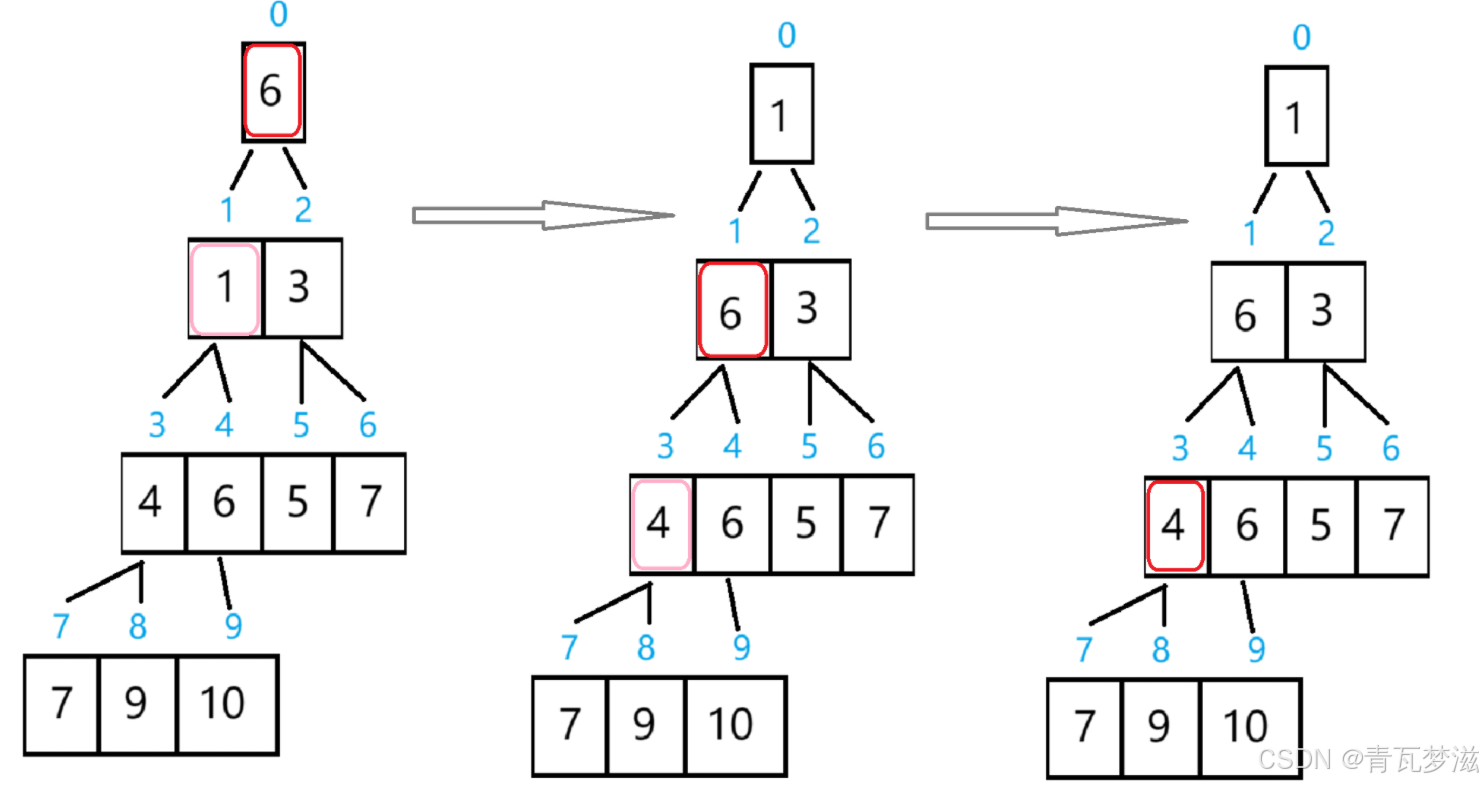到第三步时，因为它的两个孩子都没有它小，所以停止交换。

参考代码：

void AdjustDown(HPDataType* a, int n, int root)
{
	int parent = root;
	int child = root * 2 + 1;
	//父亲结点的两个孩子分别是parent*2+1和parent*2+2
	//孩子结点的父亲是(child-1)/2（因为（6-1）/2和(5-1)/2）相同（左孩子是奇数，右孩子是偶数）
	while (child < n)
	{
		//找出左右孩子中小的那一个
		if (child + 1 < n && a[child + 1] < a[child])
			++child;
		//如果孩子小于父亲，则交换
		if (a[child] < a[parent])
			Swap(a[child], a[parent])
		else
			break;
		parent = child;
		child = child * 2 + 1;
	}
}

然而这种方式有个前置条件，即根的两颗子树都已经是小（大）堆。

要想让任何一个数组都变成堆，就需要从尾部一个一个向下调整，这样向下调整过的地方都已经是小（大）堆，就符合了它的前置条件。

例如这个二叉树：

int arr[10] = { 10,9,8,7,6,5,4,3,2,1 };

即 

 这时就需要用到上面提到的孩子找父亲公式parent=(child-1)/2了

理论上从n-1开始（也就是9）也可以，但7,8,9这三个节点都是叶子结点，没有任何意义，所以为了优化，可以从(n-1 -1)/2开始（n-1是最后一个节点，再-1，/2是找父亲），这样向下调整就会从该二叉树的最后一个父亲开始

图解：

经过5次向下调整后，成功变成了小堆 ，所以建堆的时间复杂度是O(N)    (N为高度)

参考代码：

for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
	AdjustDown(a, n, i);//（此函数实现如上）
}
int end = n - 1;

堆排序：

而我们可以利用堆和向下调整这个特性来进行排序

就拿上面已经建好的堆来演示

如图所示，这是个小堆，堆顶的数据就是堆中最小的数据，现在将堆顶的数据和堆中最后一个数据（也就是n-1）交换，再将堆的大小-1，即现在这个堆里只有9个值，下标为9的那个数已经不被看做是堆里的值了。

而此时根节点就有可能不符合小堆的条件，所以需要再对根进行一次向下调整操作

如图：

 这就完成了一次置换操作

每次置换操作都会将当前堆里最小的值放到当前堆的最后

 再经过最多高度次调整后，就排成了倒序，所以堆排序的时间复杂度是O(N+N*logN)即O(N*logN)

参考代码：

void HeapSort(int* a, int n)
{
	//1.建堆
	for (int i = (n - 1 - 1) / 2; i >= 0; i--)
	{
		AdjustDown(a, n, i);
	}
	//2.排序
	int end = n - 1;
	while (end > 0)
	{
		Swap(a[end], a[0]);
		AdjustDown(a, end, 0);
		end--;
	}
}

 TopK问题：

TopK问题即：给你N个数，选出最小的前K个数

1.大多数人看到这个题的第一感觉就是用排序，排序确实可以完成，比如堆排序和快排，他们的时间复杂度是O(N*logN)

2.但我们既然学了堆，就要用到堆，比如100个数选出最小的前K个，我们可以建堆100个数小堆，这样第一个数就是当前堆里最小的数，再HeapPop（头删）9次，每次头删后堆顶的数据都是当前堆里最小的，这样就选出来了，  时间复杂度为O(N+(K-1)*logN)

这里给大家参考一下HeapPop的实现代码：

typedef int HPDataType;

typedef struct Heap
{
	HPDataType* _a;
	int _size;
	int _capacity;
}Heap;
void HeapPop(Heap* php)
{
	assert(php);
	assert(php->_size>0);
	Swap(php->_a[php->_size - 1], php->_a[0])//将堆顶数据和堆尾数据替换
	php->_size--;//再将堆的数据个数-1，这样原来堆顶的数据就无了
	AdjustDown(php->_a, php->_size, 0);//再向下调整一下
}

3.但这样还不够最优，假设N是10个亿，假设内存中存不下这些值，这些值在文件中。

假设K是10，先给前K个数建一个大堆

这样现在堆顶的数据就是目前这些数据里面最大的，然后再和下面的数一个一个比较，如果遇到比堆顶小的数据，就把这个数变成堆顶，再向下调整一遍

 

比如现在，红框的数据比堆顶要小，也就是说红框的数据更有可能是最终前K个数，所以把堆顶赋值成55，再向下调整一次

如图，现在又变成了一个大堆，如此反复再继续向下遍历，直到最后，就选出来了前K个数，堆顶的数据就是第K大的数

力扣面试题举例：

这里主要讲第三种方法，因为这也是最实用的

就拿它的示例来做演示吧

定义有

int arr={1,3,5,7,2,4,6,8};
int k=4;

 建堆：

要找出前k个数，也需要先给这个数组建小堆

 此时再和第5（也就是下标为4（k））个元素开始和堆顶比较，如果比堆顶小，就把堆顶赋值成这个数

在把4入堆后，数组后面的数就都没有堆顶的数据小了，所以4,3,2,1就是最后的结果

参考代码：

#define Swap(a,b) {int tmp=a; a=b; b=tmp;}
 void AdjustDown(int *arr,int n,int root)
 {
    int parent=root;
    int child=parent*2+1;先把左孩子看作孩子
    while(child<n)
    {
        if(child+1<n && arr[child+1]>arr[child])
            child++;//如果右孩子比左孩子要大，就把右孩子看作孩子
        if(arr[child]>arr[parent])//如果孩子比父亲大，就交换
            Swap(arr[child],arr[parent])
        else
            break;如果不是，那就说明下面就已经是堆了，就退出
        parent=child;
        child=parent*2+1;
    }
 }

int* smallestK(int* arr, int arrSize, int k, int* returnSize) 
{
    *returnSize=k;
    if(k==0)//如果k是0，直接返回NULL
        return NULL;
    int* hp=(int*)malloc(sizeof(arr)*k);
    int i;
    for(i=0;i<k;i++)
        hp[i]=arr[i];
    for(i=(k-1-1)/2;i>=0;i--)//给前k个数建堆
        AdjustDown(hp,k,i);
    for(i=k;i<arrSize;i++)//依次比较后面的数
    {
        if(hp[0]>arr[i])
        {
            hp[0]=arr[i];
            AdjustDown(hp,k,0);
        }
    }
    
    return hp;
}