Bell数-Stirling数-集合划分-整数分拆

原创于 2021-04-13 17:35:24 发布 · 1.8k 阅读

16 ·

CC 4.0 BY-SA版权

文章标签：

#Bell数 #Stirling数 #集合划分 #整数分拆

算法专栏收录该内容

48 篇文章

订阅专栏

本文探讨了集合划分的概念及其与第二类Stirling数的关系，介绍了Bell数及其递推公式，展示了Bell三角形的生成过程。同时，提到了Bell数的模素数性质，并提供了C++和Python代码实现集合划分。此外，还讨论了整数分拆的有序和无序分拆及其Ferrers图表示。

Bell数

Bell数定义

在这里插入图片描述

递推公式

在这里插入图片描述

第二类Stirling数的含义是：S(n,k)表示将n个物体划分成k个非空的不可辨别的（可以理解为盒子没有编号）集合的方法数。很明显，每一个Bell是对应的第二类Stirling数之和。
Bell数的指数生成函数是：
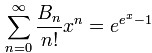
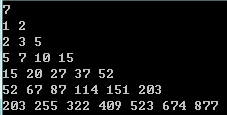
在这里插入图片描述

Bell三角形（类似于杨辉三角形）

在这里插入图片描述

#include <stdio.h>
//贝尔三角形程序
void belltriangle()
{
    int n, i, j, temp, temp2;
    scanf("%d", &n);
    int *bell = new int[n];
    bell[0] = 1;
    for (i = 1; i < n; i++)
    {
        temp = bell[0];
        bell[0] = bell[i - 1];
        for (j = 1; j <= i; j++)
        {
             temp2 = bell[j];
             bell[j] = temp + bell[j - 1];
             temp = temp2;
        }
        for (j = 0; j <= i; j++)
            printf("%d ", bell[j]);
        printf("\n");
    }
}

int main(void)
{
    belltriangle();
    return 0;
}

在这里插入图片描述

Bell数两个重要的同余性质

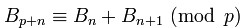
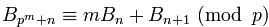
在这里插入图片描述

其中p是不大于100的素数，可以通过上面的性质来计算Bell数模小于100的素数值。
Bell数模素数p的周期为：

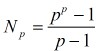
Stirling数

在数学中，斯特林数（Stirling number）用于解决各种数学分析和组合数学问题，斯特林数是两组不同的数，均是18世纪由詹姆斯·斯特林（James Stirling（mathematician））引入并以其命名，以第一类斯特林数（Stirling numbers of the first kind）和第二类斯特林数（Stirling numbers of thesecond kind）的称呼区分。此外，有时候也将拉赫数（Lah number）称为第三类斯特林数。

第一类斯特林数

定义
递推关系式
第一类斯特林数表
简单性质

第二类斯特林数

定义
递推关系式
第二类斯特林数表
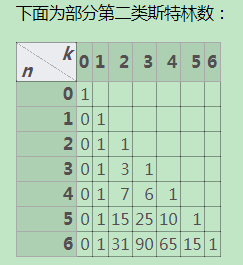
简单性质
其他性质

两类之间的关系

在这里插入图片描述

拉赫数

定义
递推关系式
拉赫数表
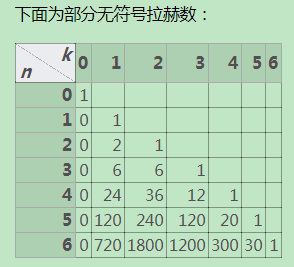
简单性质
其他性质

三类之间的关系

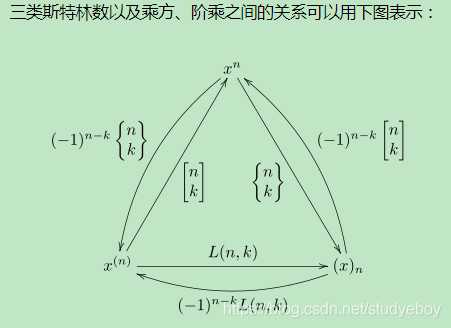
在这里插入图片描述

集合划分

集合的分划和第二类Stirling数

在这里插入图片描述

第二类Stirling数的性质

在这里插入图片描述

计算n个集合划分为非空子集的个数

int gatherRecursion(int n, int m)
{
	if (m == 1 || m == n)
	{
		return 1;
	}
	else
	{
		return m * gatherRecursion(n - 1, m) + gatherRecursion(n - 1, m - 1);
	}
}
int main(void)
{
	int gatherElement = 4;
	int sum = 0;
	for (int i = 1; i <= gatherElement; i++)
	{
		int result = gatherRecursion(gatherElement, i);
		sum = sum + result;
		printf("gatherNum(%d, %d) = %d\n", gatherElement, i, result);
	}
	printf("集合%d的所有划分数为： %d\n", gatherElement, sum);
	system("pause");
	return 0;
}

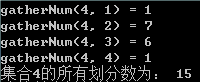
在这里插入图片描述

n个集合划分为非空子集的所有划分方式

C++版本

#include <iostream>
#include <fstream>
using namespace std;
void printarr(int tab[], int n);
void part_gen(int tab[], int n);
bool check(int tab[], int n);
fstream file;
int main() {
	cout << "Program that counts possible partitions of a set" << endl;
	int n;
	cout << "\nPlease give n: ";
	cin >> n;
	int *tab = new int[n];
	for (int i = 0; i < n; i++) {
		tab[i] = 1;
	}
	file.open("MP_L2.txt", fstream::out);
	printarr(tab, n);
	int counter = 1;
	while (tab[n - 1] != n) {
		part_gen(tab, n);
		printarr(tab, n);
		counter++;
	}
	cout << endl <<"There are "<< counter<<" possible partitions of a set"<<endl;
	file<< endl << "There are " << counter << " possible partitions of a set" << endl;
	delete[]tab;
	file.close();
	system("pause");
	return 0;
}
void part_gen(int tab[], int n)
{
	if (check(tab, n)) {
		tab[n - 1]++;
	}
	else
	{
		part_gen(tab, n - 1);
		for (int i = n - 1; i < n; i++)
			tab[i] = 1;

	}

}
void printarr(int tab[], int n)
{
	for (int i = 0; i < n; i++) {
		cout << tab[i] << " ";
		file << tab[i] << " ";
	}
	file << "\n";
	cout << endl;
}
bool check(int tab[], int n)
{
	for (int i = 0; i < n - 1; i++) {
		if (tab[i] == tab[n - 1])
			return true;

	}
	return false;
}

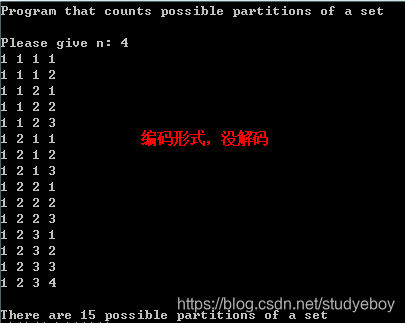
在这里插入图片描述

Python 版本

def partitions(set_):
    if not set_:
        yield []
        return
    for i in range(int(2**len(set_)/2)):
        parts = [set(), set()]
        for item in set_:
            parts[i&1].add(item)
            i >>= 1
        for b in partitions(parts[1]):
            yield [parts[0]]+b

for p in partitions(["1", "2", "3", "4"]):
    print(p)