树形DP+容斥原理（处理树上染色问题）

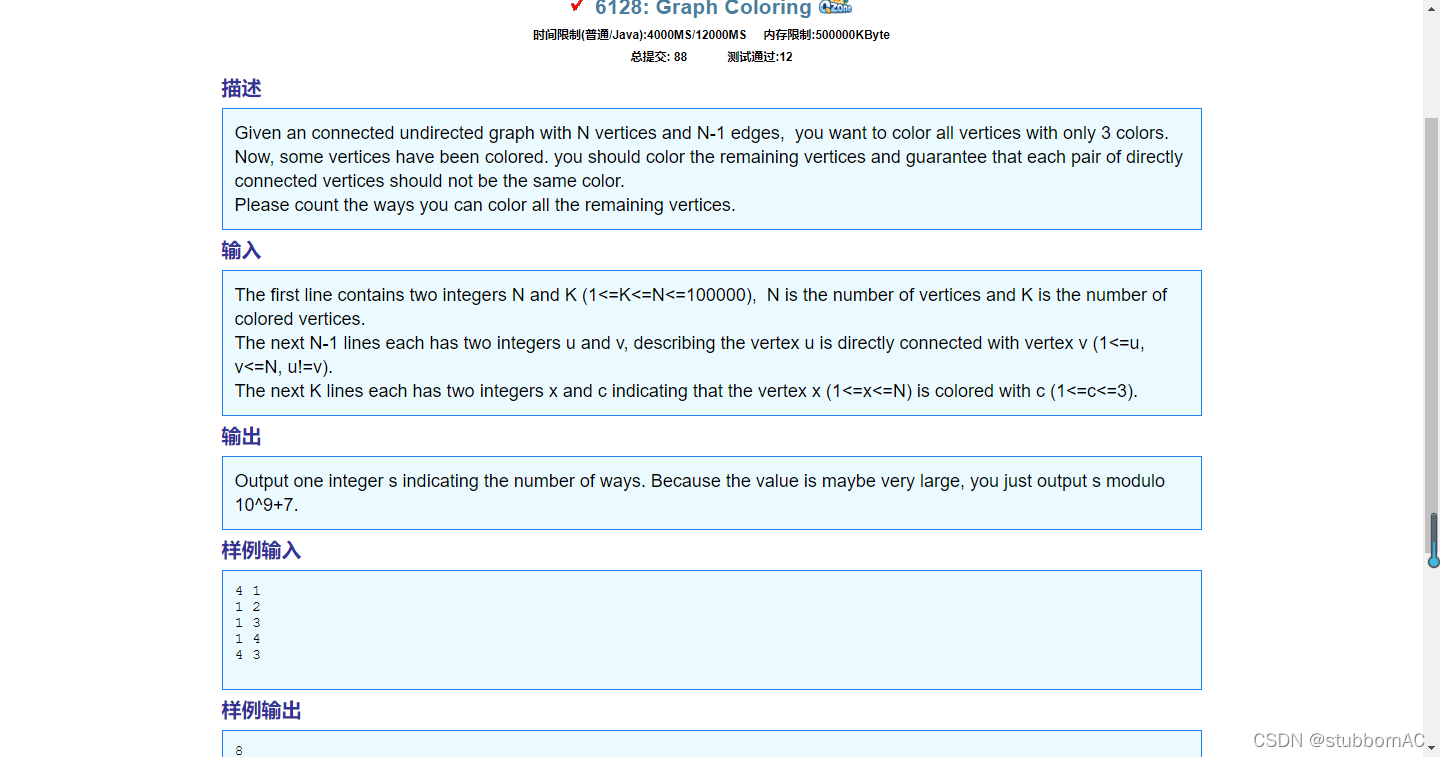
这题的题意大概就是给定一个具有 N 个顶点和 N-1 条边的连通无向图，只用 3 种颜色为所有顶点着色。 现在，一些顶点已被着色。您应该为剩余的顶点着色，并保证每对直接连接的顶点不应该是相同的颜色。请计算所有剩余顶点着色的方案数取模10^9+7。
一眼树形DP题：三种情况
1.//有父亲节点的点的方案数
2.已经染色的节点的方案数
3/独立节点的方案数
分开处理就好

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

inline ll read(){
   
   
    ll x=0,f=1;
    char ch=getchar();
    while(ch<'0'||ch>'9'){
   
   
        if(ch=='-')
            f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9'){
   
   
        x=(x<<1)+(x<<3)+(ch^48);
        ch=getchar();
    }
    return x*f;
}
vector<ll>vec[100005],vec2;//vec用来构建图，也可以用链式前向星，ve2用来记录已经染色的点
int vis[100005];//标记已经染色的点的颜色
int son[100005];//标记父亲节点的颜色
ll dp[4][100005];//记录三种颜色各自的方案数
const ll mod=1e9+7