机器学习入门（4）——逻辑回归（Logistic Regression）

分类问题（Classification）

在分类问题中，要预测的变量 y是离散的值。逻辑回归 (Logistic Regression) 的算法是目前最流行使用最广泛的一种学习算法，它算法的性质是：输出值永远在0到 1 之间。
逻辑回归算法实际上是一种分类算法，它适用于标签 y取值离散的情况。

假设陈述（Hypothesis Representation）

我们引入一个新的模型，逻辑回归，该模型的输出变量范围始终在0和1之间。 逻辑回归模型的假设是：$h_{\theta }(x)=g\left({\theta }^{T}X\right)$。其中：X代表特征向量，g代表逻辑函数（logistic function)，是一个常用的逻辑函数为S形函数（Sigmoid function），公式为：$g(z)=\frac{1}{1+e^{-z}}$。
该函数的图像为：

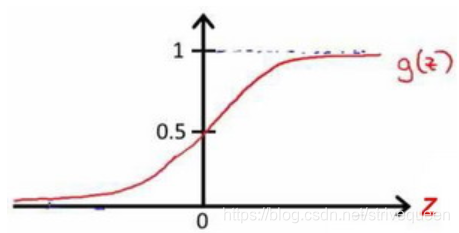
python代码实现：

import numpy as np
    
def sigmoid(z):
    
   return 1 / (1 + np.exp(-z))

对模型的理解：
$h_{\theta }(x)$的作用是，对于给定的输入变量，根据选择的参数计算输出变量=1的可能性（estimated probablity）即$h_{\theta }(x)=P(y=1\mid x;\theta )$。例如，若对于给定的x，通过已经确定的参数计算得出$h_{\theta }(x)$=0.7，则表示有70%的几率y为正向类，相应地y为负向类的几率为1-0.7=0.3。

决策界限（Decision Boundary）

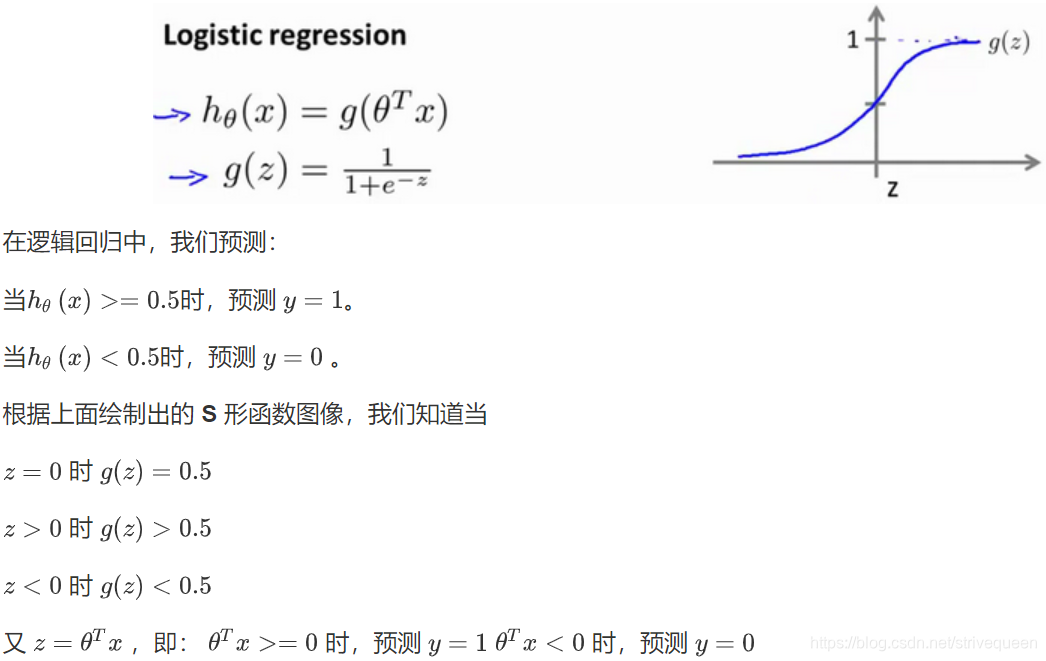
代价函数（Cost Function）

对于线性回归模型，我们定义的代价函数是所有模型误差的平方和。理论上来说，我们也可以对逻辑回归模型沿用这个定义，但是问题在于，当我们将$h_{\theta }(x)=1+e^{-}$