前言
这一章还是紧接着上一章的内容,从这一章开始,给大家介绍回归问题的另一个问题,classification(分类)问题,即我们在第一章就跟大家介绍过,这个结果是离散的。下面会跟大家进行详细的分析!
最后,如果内容有什么错误的理解,希望大家不吝赐教,指正,谢谢!
【机器学习系列】【第三章:多元变量的线性回归问题】【第五章:正则化】
第四章 Logistic Regression(逻辑回归)
4.1 classification(分类)
例如把一封收到的邮件归为垃圾邮件还是非垃圾邮件,判断一个肿瘤是良性还是恶性,等等,这些都是classification问题,关于这些的结果,我们都可以用0和1来表示,,下面用Tumor size(肿瘤的大小)和预测结果是恶性还是良性问题来跟大家详细分析。
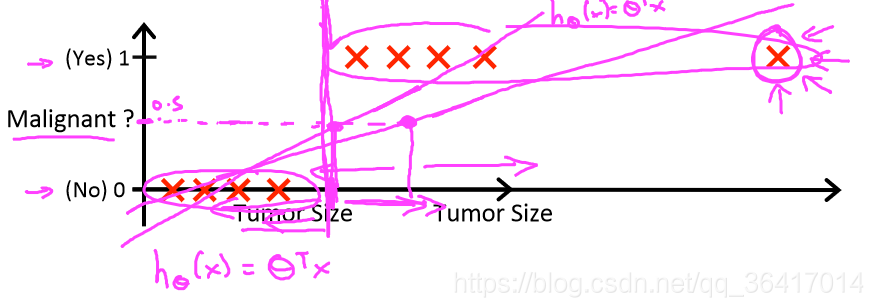
图1 Tumor size和Malignant?
如图1所示,关于Tumor size和Malignant?问题,我们假设h(x)=来模拟两者之间的关系,h(x)是一个线性关系,一般情况下,我们都是以0.5作为阈值,即当h(x)<0.5时,y=0;当h(x)>=0.5时,y=1。分类的结果只有0和1,而从图中可以看出h(x)的结果是可以超过1的或者小于0的,表示我们所选的函数关系不够好,但对于classification regression来讲:0<=h(x)<=1的,所以下面我们对于h(x)的表达式会进行详细的分析。
4.2 Hypothesis Representation(关于h(x)的表达式)
对于h(x)来讲,我们需要的是希望h(x)的范围在0~1之间,在前面我们假设h(x)=,但显然h(x)的范围会超过0~1,所以我们令g(z)=
,其中z=
,所以h(x)=
。而g(z)的图像如图2所示,可以看出0<=g(z)<=1。我们把这个函数也称为logistic function(逻辑函数)或者Sigmoid function(S型函数)。
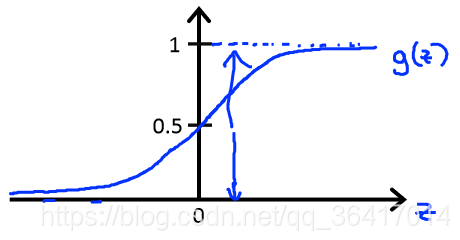
图2 g(z)的图像
关于h(x)=a也有了新的含义,即当输入为x时,输出为y=1的概率为a,也可以表示为P(y=1|x;)=a,则我们会有
P(y=1|x;)+P(y=0|x;
)=1,所以P(y=0|x;
)=1-P(y=1|x;
)。
4.3 Decision boundary(决策边界)
回到前面我们所讨论的阈值问题,当h(x)<0.5时,判断为y=0;当h(x)>=0.5时,判断为y=1;对于现在这个新的函数h(x)如图2所示,当z<0时,h(z)<0.5;当z>=0时,h(z)>=0.5。即当<0时,h(x)<0.5,y=0;当
>0时,h(x)>=0.5,y=1。
下面用几个实际的例子来向大家展现怎样来区分y=0和y=1,这个决策的边界是什么样的。
1)线性关系的决策边界
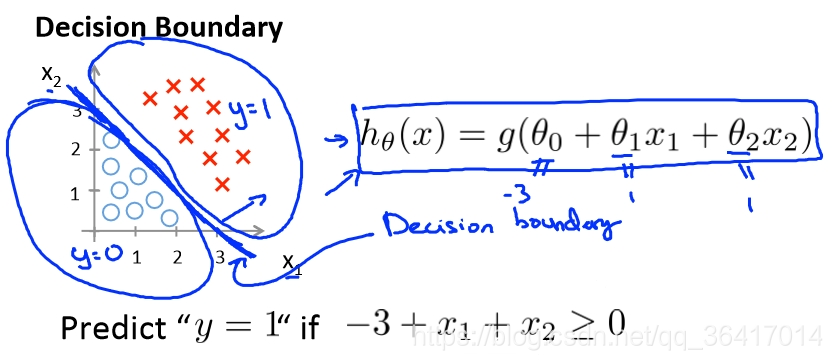
图3 linear decision boundary
如图3所示,在这个问题中=
,在这个问题中,我们先告诉大家
0=-3,
1=1,
2=1(至于这个值是怎么得到的,我们后面会有详细的介绍),即
=-3+x1+x2,如果我们预测结果为y=1,即需要
>=0,即-3+x1+x2>=0,得到x1+x2>=3,在图中画出x1+x2=3这条直线,就是我们所求的Decision boundary(决策边界),在这条直线的右上部分即是预测结果为y=1的部分。
2)非线性关系的决策边界
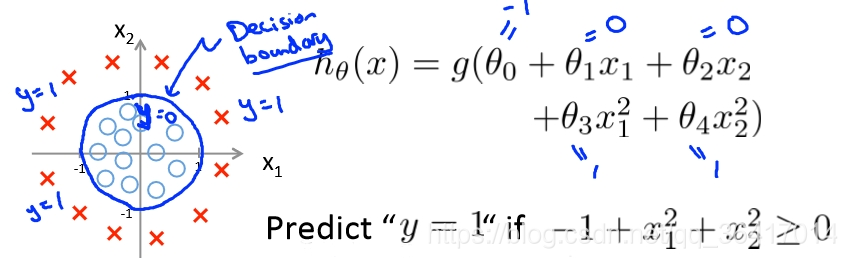
图4 non-linear decision boundary
在图4中可以看出,=
,在这里我们同样告诉大家
0=1,
1=0,
2=0,
3=1,
4=1,这个时候
=-1+
,当-1+
>=0时,即
>=1,如图4中的所画的圆,就是我们需要的决策边界,在圆外的就是y=1部分,而圆内的就是y=0部分,从这个问题可以看出决策边界并不只是直线,甚至也不只是这个规矩的圆,可以是任意的形状,只要能把我们的两类数据分离开来就行。
4.4 Cost Function(代价函数)
关于如何选取,我们就不得不提Cost Function,在前面讨论regression问题时,我们就用到了Cost Function,在这里我们同样也需要用到它,它仍然是我们用来评判
选取是否合适的一个标准。
在前面我们对Cost Function的定义是J()=
,我们把
移到求和里面,这个时候式子成了J(
)=
,我们再用Cost(h(x),y)来代替
,Cost(h(x),y)=
,其中h(x)=
。
这个对于线性回归问题是很好的,但现在问题是逻辑回归问题,如果我们继续用这个定义,我们会发现J()和
的关系如图5所示
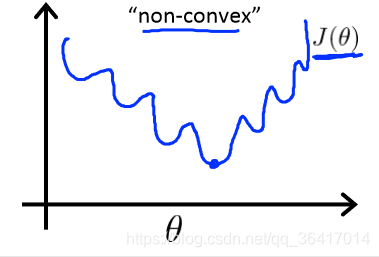
图5 non-convex
在图5中,我们会发现,J()存在很多的局部最小值,在前面也跟大家介绍过,一旦找到一个局部最小值,则不会再改变,所以对于这个来看,很难找到J(
)对于整个
来讲的一个最小值。所以我们希望J(
)是如图6所示的这样,是一个平缓的凸面。
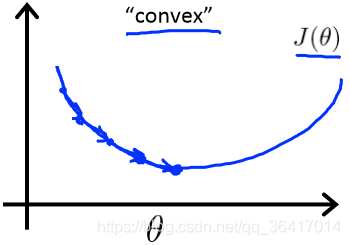
图6 convex
所以对于以上这个问题,我们对Cost(h(x),y)进行了一些改变,对Cost(h(x),y)重新定义
1)当y=1时,我们会得到如图7所示,当h(x)=1时,Cost(h(x),y)=0,而当h(x)0时,Cost(h(x),y)
,即if h(x)=0,
P(y=1|x;)=0,但是y=1时,我们会有一个很大的cost。
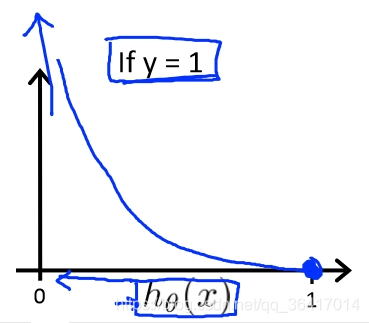
图7 y=1时 Cost(h(x),y)和h(x)的关系
2)当y=0时,我们会得到如图8所示,当h(x)=0时,Cost(h(x),y)=0,而当h(x)1时,Cost(h(x),y)
,正好与y=1时相反。
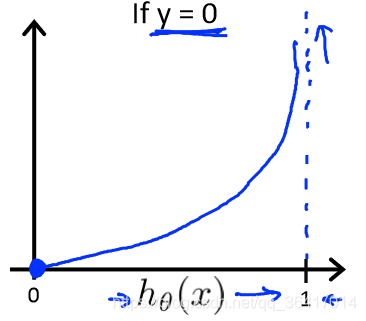
图8 y=0时, Cost(h(x),y)和h(x)的关系
4.5 Simplified cost function and gradient descent(简化代价函数和梯度下降)
在前面,我们得到了,
,
Note:y=0 or y=1 always:,so
,To fit parameters
:minJ(
),To make a prediction given new x:output h(x)=
。
关于该如何选取,和前面一样,我们有
(其中h(x)=
),记住同时更新
。对于
,我们需要计算的有J(
)和
。而对于这些需要计算的变量,我们·有几个算法用来计算这些,如Gradient descent、Conjugate gradient、BFGS、L-BFGS,第一个也是我们一直以来使用的算法,而对于后面的三个,优点就是不需要选择learning rata(
),收敛速度要比Gradient descent速度要快,但缺点是更复杂,所以在争对我们这个刚开始学习来说,用比较简单的算法就可以了,后面等学到了一定的深度,大家可以有兴趣地了解下其他的算法。
下面给大家介绍下如何用Octave这个软件来根据已知条件求出,给大家一个例子来说明问题。
,
,我们对J(
)关于
分别求1偏导有:
,
Octave:
function [jval,gradient]=costFunction(theta)
jval=(theta(1)-5)^2+(theta(2)-5)^2;
gradient=zeros(2,1);
gradient(1)=2*(theta(1)-5);
gradient(2)=2*(theta(2)-5);
options = optimset('GradObj', 'on', 'MaxIter', 100); %MaxIter should be an integer
initialTheta = zeros(2,1);
[optTheta, functionVal, exitFlag] = fminunc(@costFunction, initialTheta, options);
4.6 One-vs-all(一对多)
在我们实际问题中,我们很多的分类不只有两种,比如明天的天气,是多云、晴天、下雨等等,或者邮件的分类可以是朋友、家人、兴趣等等,我们会发现结果是多个的,这就是接下来我要给大家介绍的一对多的问题(注意一下,跟前面章节所讲的linear regression问题注意区分,虽然这个结果也是多种,但是离散的,而前面所讨论的结果是连续的)
关于结果只有两类的问题,我们只需要进行一次分类即可,如图9所示。
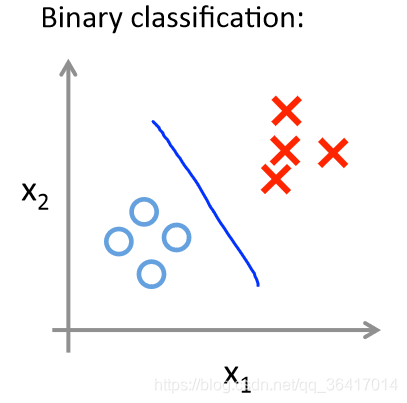
图9 Binary classification
而对于多类的问题,我们需要如何进行分类了?如图10所示。
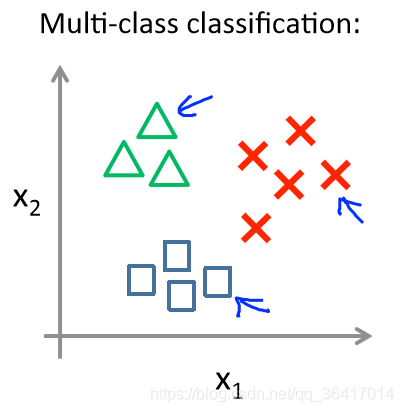
图10 Multi-class classification
而对于这个问题,我们可以进行如图11所示,进行单个分类,即我们需要把哪一类分离出来,则把其他的都看作同一类即可,这个时候就变成了Binary classification问题,则可以按照上面的方法进行分类。如果需要分类的类别是n(n>2),则需要进行n次分类。
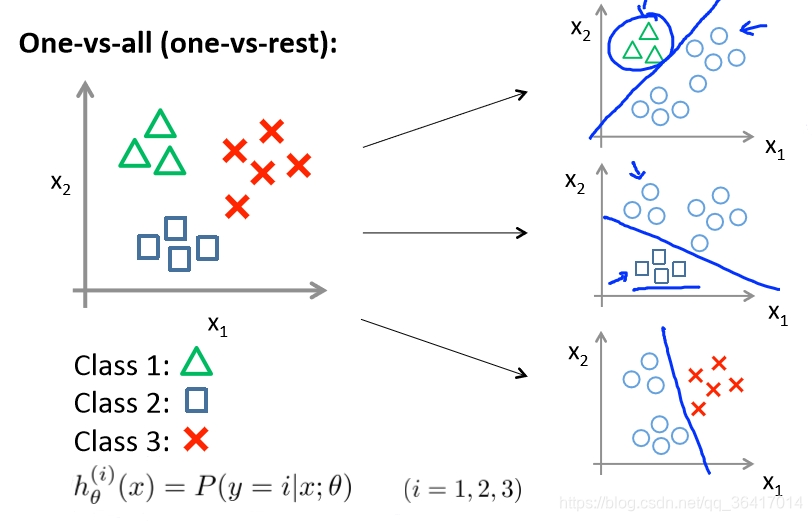
图11 One-vs-all








 本文深入探讨了逻辑回归在分类问题中的应用,介绍了如何通过逻辑函数实现0和1的预测,解析了决策边界的形成,并对比了线性和非线性决策边界的特性。此外,还讨论了代价函数在参数选择中的作用,以及简化代价函数和梯度下降法的应用。
本文深入探讨了逻辑回归在分类问题中的应用,介绍了如何通过逻辑函数实现0和1的预测,解析了决策边界的形成,并对比了线性和非线性决策边界的特性。此外,还讨论了代价函数在参数选择中的作用,以及简化代价函数和梯度下降法的应用。

















 496
496

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










