介绍
最近看了一篇文章,Yanchi Liu等人比较了各个聚类评价指标(例如??, ?, ??, ??以及S_Dbw等等),在一些有着不同挑战的数据集上(例如有噪声,密度不均,某几类挨得比较近等等问题),比较了几种评价指标选择不同聚类算法中超参的能力。
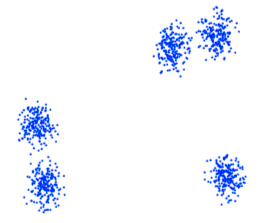
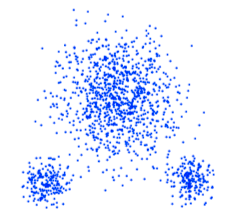
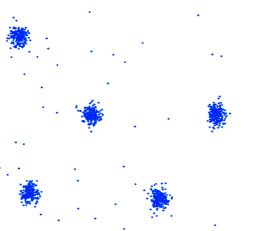
其中比较结果如下:
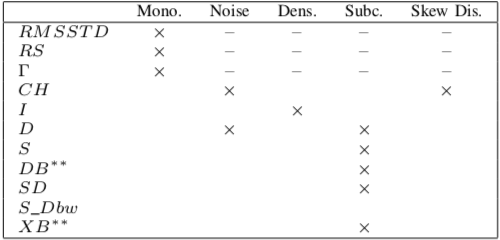
列代表不同的聚类评价指标,行代表数据集中存在的不同扰动挑战,其中标志x代表该评价指标对这种扰动选择聚类的超参失效了,符号-代表没有对该种情况进行测试,观察可以发现评价指标S_Dbw对于各种噪声,不同密度的数据集等等干扰项来选择超参的鲁棒性最强,网上搜了下没有相关的实现,自己实现了下, python代码在这里。
S_Dbw
S_Dbw是由两项组成,分别是簇间密度( ( 1.1 ) (1.1) (1.1))和簇内方差( ( 1.2 ) (1.2) (1.2)),使用它评价选取不同参数下的聚类算法结果时,取S_Dbw值最小的一组参数即可。
(1.1) D e n s _ b w ( c ) = 1 c ⋅ ( c − 1 ) ∑ i = 1 n ( ∑ j = 1 i ≠ j c d e n s i t y ( u i j ) max ( d e n s i t y ( v i ) , d e n s i t y ( v j ) ) ) Dens\_bw(c) = \frac{1}{c\cdot(c-1)}\sum_{i=1}^{n}(\sum_{{{j=1}\atop{i\neq{j}}}}^{c}\frac{density(u_{ij})}{\max(density(v_i), density(v_j))}) \tag{1.1} Dens_bw(c)=c⋅(c−1)1i=1∑n(i̸=jj=1∑cmax(density(vi),density(vj))density(uij))(1.1)
(1.2) S c a t ( c ) = 1 c ∑ i = 1 c ∥ δ ( v i ) ∥ ∥ δ ( S ) ∥ Scat(c) = \frac{1}{c}\sum_{i=1}^{c}\frac{\left\|\delta(v_i)\right\|}{\left\|\delta(S)\right\|} \tag{1.2} Scat(c)=c1i=1∑c∥δ(S)∥∥δ(vi)∥(1.2)





 本文深入探讨了S_Dbw作为一种聚类效果评价指标的优越性,特别是在面对复杂数据集,如存在噪声、密度不均等问题时,其在选择聚类算法超参数方面的鲁棒性表现突出。S_Dbw由簇间密度和簇内方差两部分组成,通过最小化S_Dbw值来确定最优聚类参数。
本文深入探讨了S_Dbw作为一种聚类效果评价指标的优越性,特别是在面对复杂数据集,如存在噪声、密度不均等问题时,其在选择聚类算法超参数方面的鲁棒性表现突出。S_Dbw由簇间密度和簇内方差两部分组成,通过最小化S_Dbw值来确定最优聚类参数。
















 788
788

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








