关于Critic确定权重的matlab代码和python代码

关于Critic确定权重的matlab代码和python代码：

观察到关于Critic确定权重的相关知识比较少，笔者写了一点自己的理解，如果有不对的地方还请指教！另外文章最后给出我自己写的matlab代码和python代码！

本文采用CRITIC 赋值法对模型进行优化。Critic 赋值法以两个基本概念为基础：一是对比强度，借鉴标准离差法的思想,认为若同一指标的所有评价指数差别越大，即标准差越大，则所蕴含的信息量越大；二是评价指标之间的冲突性,指标之间的冲突性是以指标之间的相关系数为基础，如两个指标之间具有较强的正相关，说明两个指标冲突性较低。第j 个指标与其它指标的冲突性的量化指标 ，其中𝑟𝑖𝑗评价指标i和j之间的相关系数。各个指标的客观权重确定就是对比强度和冲突性来综合衡量的。设𝐶𝑗表示第j个评价指标所包告的信息量。𝐶𝑗的计算式:

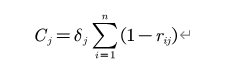
一般地，𝐶𝑗越大，第j个评价指标所包含的信息量越大，则该指标的相对重要性也就越大。设𝑊𝑗为第j个指标的客观权重。𝑊𝑗的计算公式：

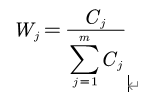
（m为指标数（维度），n为样本个数）

Critic算法流程图：

例题：假设有下面的数据：（例题参考自：https://www.docin.com/p-847838688.html）
资产收益率 费用利润率 逾期贷款率 资产使用率 自有资本率
中信银行 0.4830 13.2682 0.0000 4.3646 5.1070
光大银行 0.4035 13.4909 39.0131 3.6151 5.5005
浦发银行 0.8979 25.7776 9.0513 4.8920 7.5342
招商银行 0.5927 16.0245 13.2935 4.4529 6.5913
注：逾期贷款率为越小越好，其余为越大越好；

经过极大化指标和标准化数据后得到以下矩阵（这里采取的是最大值最小值标准化）：
资产收益率 费用利润率 逾期贷款率 资产使用率 自有资本率
中信银行 0.16800 0.0000 1.0000 0.58697 0.0000
光大银行 0.00000 0.01780 0.0000 0.00000 0.16212
浦发银行 1.00000 1.00000 0.76799 1.00000 1.00000
招商银行 0.38269 0.22034 0.65926 0.65612 0.61153

相关矩阵为：

标准化后的各列标准差：

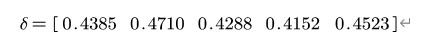
最后求得各指标的权重为：

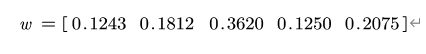
Matlab代码：

clc;clear;
X=[0.4830,13.2682,0.0000,4.3646,5.1070;
0.4035,13.4909,39.0131,3.6151,5.5005;
0.8979,25.7776,9.0513,4.8920,7.5342;
0.5927,16.0245,13.2935,4.4529,6.5913];
[n,m]