【OCCT+ImGUI系列】011-Poly-Poly_Triangle三角形面片

Poly_Triangle 是什么？

Poly_Triangle 是一个非常轻量的类，用于表示一个三角网格中的单个三角形面片。它是构成 Poly_Triangulation（三角网格对象）的基本单位之一。之后会写关于碰撞检测的相关文章，三角面片是非常重要的一部分。

每个 Poly_Triangle 包含三个整数索引，它们是指向一个节点列表的索引（通常是 Poly_Triangulation::Nodes() 中的点）。这些节点是三角形的三个顶点。

---

🔹 数据成员

Standard_Integer myNodes[3];

• 存储三个节点的索引，索引范围通常是 [1, NbNodes()]（注意：OpenCascade 中使用 1-based 索引）。
• 每个索引指向的是一个顶点坐标，坐标存储在 Poly_Triangulation 中的节点数组里。

---

🔹 构造函数

Poly_Triangle()

• 默认构造函数，三个索引值初始化为 0（无效状态）。

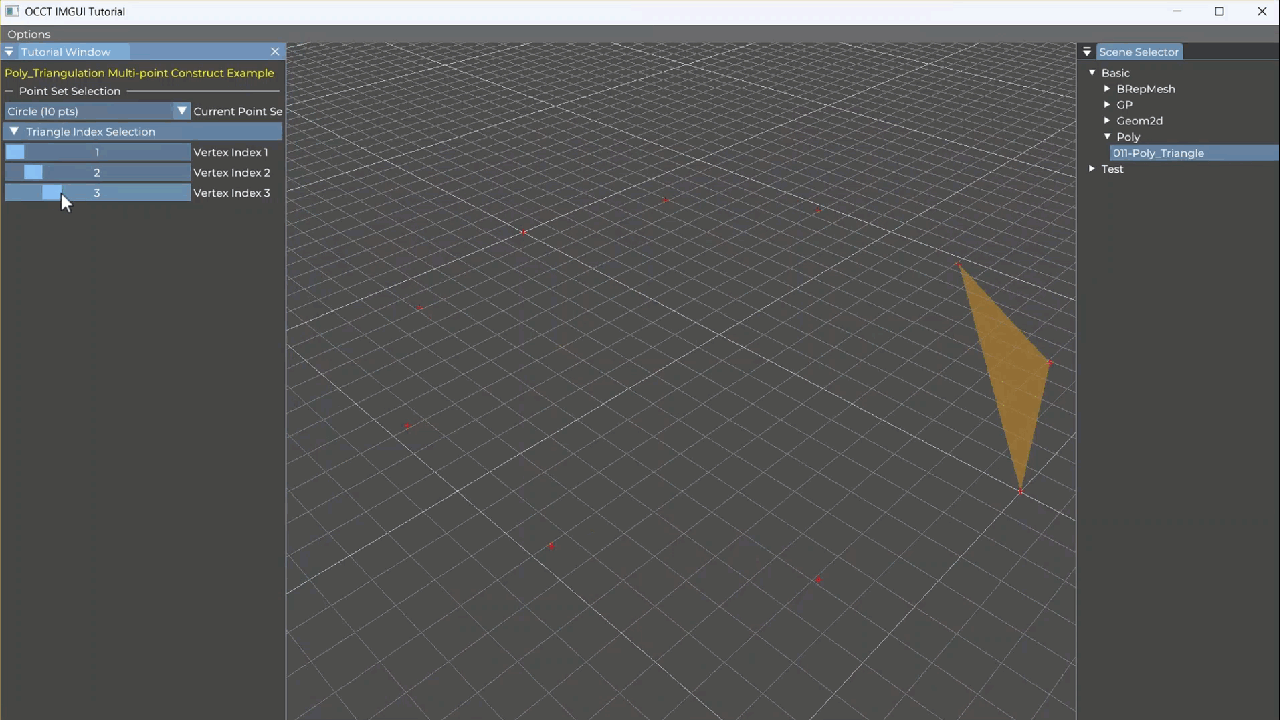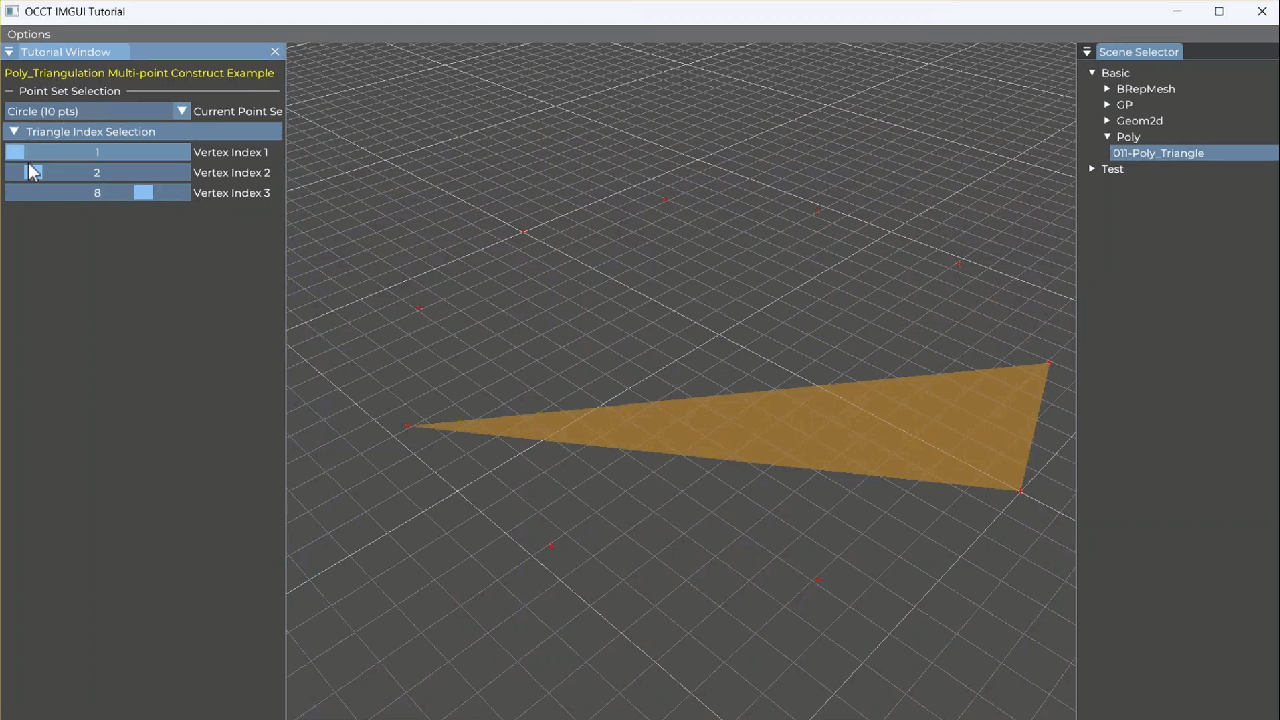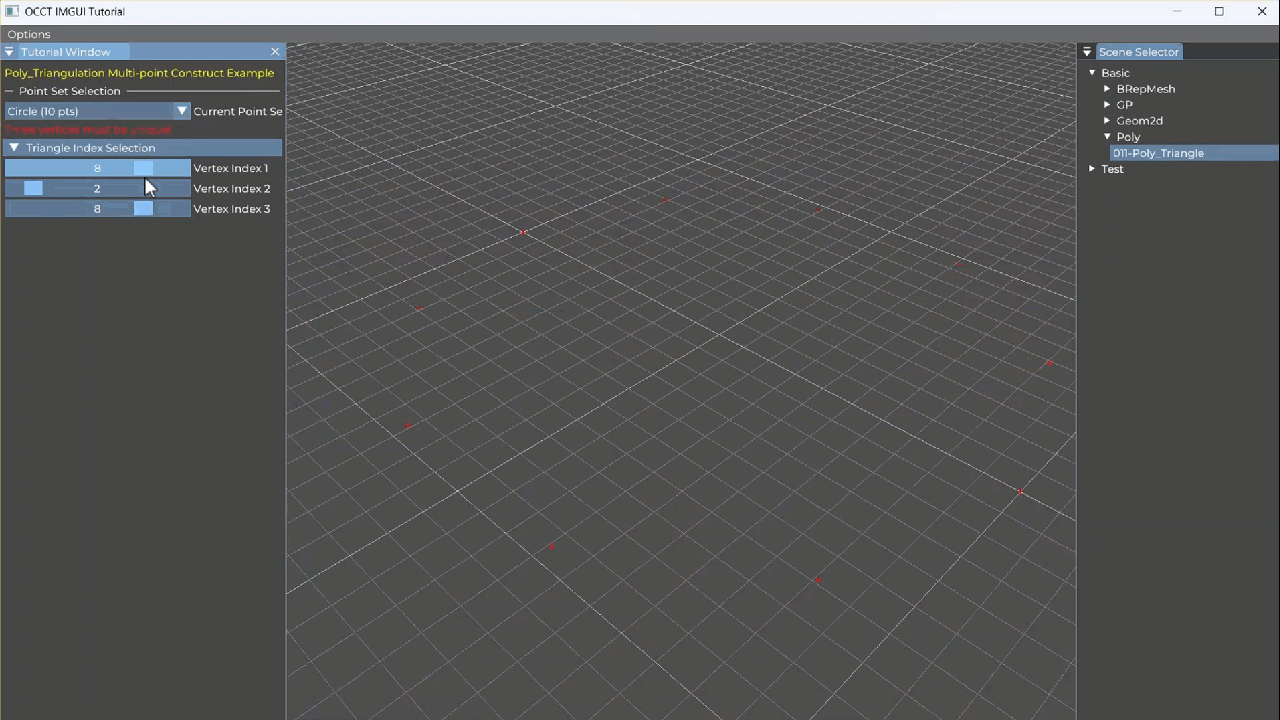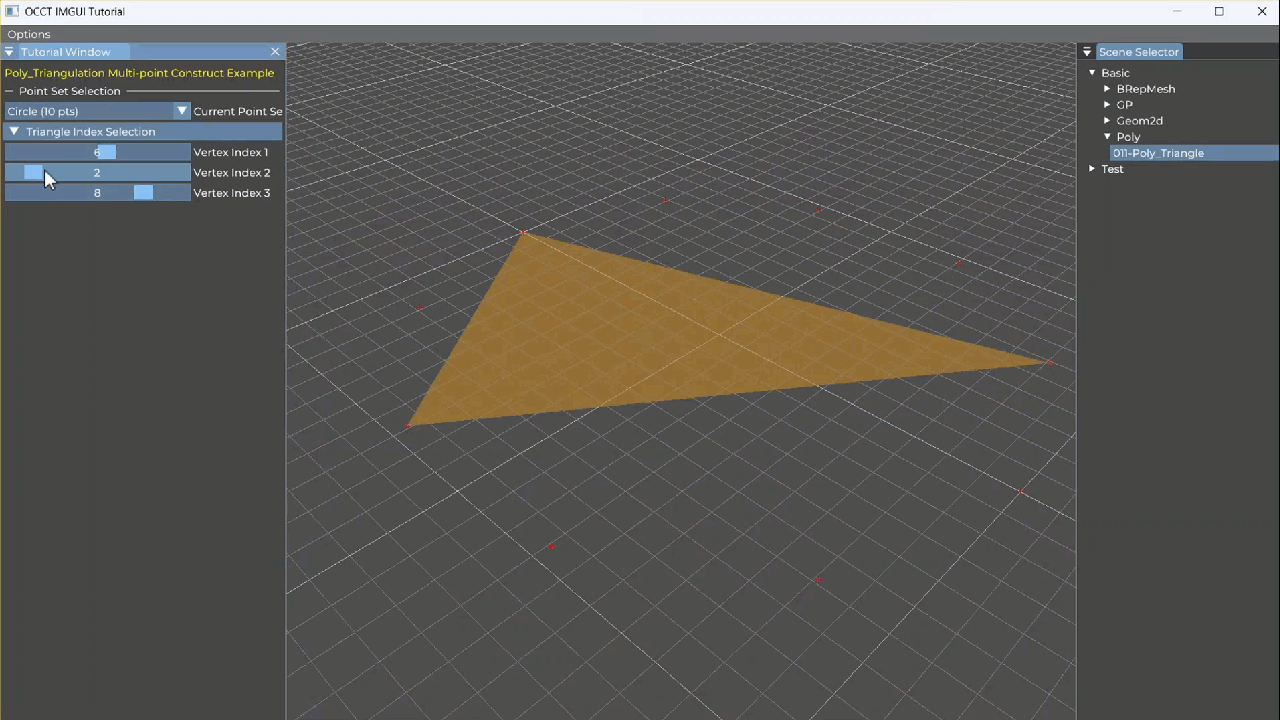
如图为从点击选择三个点的索引来构造Poly_Triangle并显示。

Poly_Triangle(Standard_Integer theN1, Standard_Integer theN2, Standard_Integer theN3)

• 构造函数，直接设置三个顶点索引。

---

🔹 成员函数

设置节点索引

void Set(Standard_Integer theN1, Standard_Integer theN2, Standard_Integer theN3)

• 一次性设置所有三个节点索引。

void Set(Standard_Integer theIndex, Standard_Integer theNode)

• 设置指定位置（1~3）的单个索引值。
• 如果 theIndex 不在 1~3，抛出 Standard_OutOfRange 异常。

---

访问节点索引

void Get(Standard_Integer& theN1, Standard_Integer& theN2, Standard_Integer& theN3) const

• 返回三个节点索引的值（通过引用）。

Standard_Integer Value(Standard_Integer theIndex) const

• 返回指定位置（1~3）的节点索引值，超出范围抛异常。

Standard_Integer operator()(Standard_Integer theIndex) const
Standard_Integer& operator()(Standard_Integer theIndex)

• 函数调用操作符的重载，提供类似数组访问的方式。
• 返回索引值（常量或引用）。

Standard_Integer& ChangeValue(Standard_Integer theIndex)

• 返回对某个节点索引的引用，可以进行原地修改。

注意点

1. 索引范围是 1~NbNodes()，不是从0开始。
2. 三角形只保存的是节点索引，不保存具体的几何位置，顶点坐标保存在 Poly_Triangulation 中。
3. 修改 Poly_Triangle 不会自动更新 Poly_Triangulation，需要你在使用时保持一致性。

---

总结

功能	方法	简述
构造	Poly_Triangle()	空三角形
构造	Poly_Triangle(n1,n2,n3)	初始化三角形索引
访问	Get()	获取3个顶点索引
访问	Value(index) / operator()	获取某个索引值
修改	Set(n1,n2,n3) / Set(index, node)	设置索引
修改	ChangeValue(index)	引用访问可直接修改

代码

#pragma once

#include "pch.h"
#include <Poly_Triangulation.hxx>
#include <AIS_Triangulation.hxx>
#include <BRepBuilderAPI_MakeVertex.hxx>
#include "BaseScene.h"
#include "VisSceneComponents.h"
#include "TutorialWindow.h"

class PolyTriangle011 : public BaseScene, public VisSceneComponents, public TutorialWindow {
   
   
public:
    PolyTriangle011() {
   
   
        openTutorialWindow();
        initAllNodes()