算法设计与分析 —— 排列问题

问题描述

设计一个递归算法生成n个元素$r_1,r_2,...,r_n$的全排列

• 设$R=r_1,r_2,...,r_n$是要进行排列的n个元素，$R_i=R-r_i$。
• 集合$X$中元素的全排列记为$perm(X)$
• $(r_i)perm(X)$表示在全排列$perm(X)的每一个排列前加上前缀得到的排列

R的全排列可归纳定义如下：

• 当$n=1$时，$perm(R)=(r)$，其中r是集合R中唯一的元素；
• 当$n>1$时，$perm(R)$由$(r_1)perm(R_1),(r_2)perm(R_2),...,,(r_n)perm(R_n)$构成。

---

算法思路

• 递归过程：将规模为 $n$ 的全排列问题转化为规模为 $n-1$ 的全排列问题。故全排列可以看做固定 $[0,k]$ 位，对 $[k+1,n]$位进行全排列，当 $k+1=n$时，递归结束。

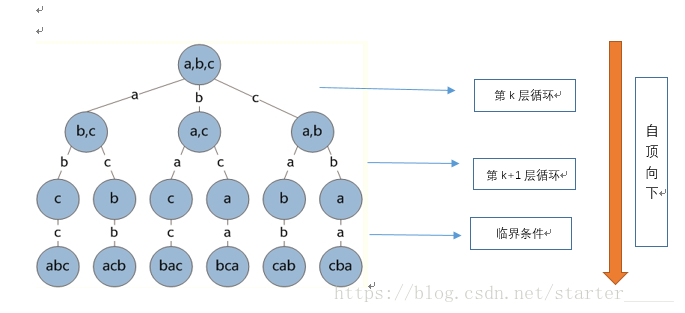
• 第 $k$ 层的循环是第 $k$ 位与它自身及后面的非重复元素交换，然后对前 $k$ 位进行固定，进入 $k+1$ 层的循环。

---

算法效率

假设递归算法所需的计算时间为$T(n)$，则：

• $T(1)=O(1)$
• $T(n)=n\ast T(n-1)+O(1)$

解得：$T(n)=O(n!)$

---

代码实现

#include <iostream>
using namespace std;
#define length 3

template<typename T>
inline void Swap(T &a,T &b)
{
    T temp=a;
    a=b;
    b=temp;
}

template<typename T>
void Perm(T list[],int k,int m)// 产生list[k:m]的所有排列
{
    if(k==m){// 只剩下一个元素
        for(int i=0;i<=m;i++){
            cout<<list[i];
        }
        cout<<endl;
        return 0;
    }
    for(int i=k;i<=m;i++){
        Swap(list[k],list[i]);
        Perm(list,k+1,m);
        Swap(list[k],list[i]);
    }
}
template<typename T>
bool findSame(T list[],int k,int i)//list[i]元素与list[k,i-1]的元素重复时返回true，否则返回false。
{
    for(int f=k;f<i;f++){
        if(list[f]==list[i]){
            return true;
        }
    }
    return false;
}

template<typename T>
void PermExcludeSame(T list[],int k,int m)// 产生list[k:m]的所有排列
{
    if(k==m){// 只剩下一个元素
        for(int i=0;i<=m;i++){
            cout<<list[i];
        }
        count++;
        cout<<endl;
    }
    for(int i=k;i<=m;i++){
        if(findSame(list,k,i)){
            continue;
        }
        Swap(list[k],list[i]);
        PermExcludeSame(list,k+1,m);
        Swap(list[k],list[i]);
    }
}
int main()
{
    char list[length]={'a','b','c'}; //不带重复元素
    Perm(list,0,length-1);
	char list[length]={'a','c','c'}; //带重复元素
	PermExcludeSame(list,0,length-1);
    return 0;
}