以K近邻回归模型为例,说明偏差-方差权衡。某数据点的预测函数值为该点K个最近邻实例输出的平均值:
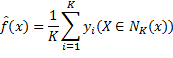
因此预测函数的方差等于:
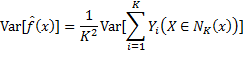
因为各实例的输出Yi是独立的随机变量,且它们的方差都等于σ^2,所以


 本文以K近邻回归为例,探讨偏差-方差权衡问题。K值增加,预测函数方差减小,偏差增大,模型趋于平滑;反之,方差增大,偏差减小,但易过拟合。K值选择影响模型复杂度,过高可能导致过拟合,过低则可能欠拟合。正则化是避免过拟合的一种技术,通过约束模型参数来平衡偏差与方差。高维空间中,K近邻模型的偏差会因样本稀疏而增大。
本文以K近邻回归为例,探讨偏差-方差权衡问题。K值增加,预测函数方差减小,偏差增大,模型趋于平滑;反之,方差增大,偏差减小,但易过拟合。K值选择影响模型复杂度,过高可能导致过拟合,过低则可能欠拟合。正则化是避免过拟合的一种技术,通过约束模型参数来平衡偏差与方差。高维空间中,K近邻模型的偏差会因样本稀疏而增大。
以K近邻回归模型为例,说明偏差-方差权衡。某数据点的预测函数值为该点K个最近邻实例输出的平均值:
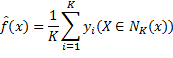
因此预测函数的方差等于:
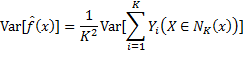
因为各实例的输出Yi是独立的随机变量,且它们的方差都等于σ^2,所以


 435
435


 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


