prim模板（以及洛谷p1265）

prim算法
从图中选一个点作为起点，利用贪心的思想，寻找这个点最近的一个点并相连　设G = (V,E)是连通带权图，U是V的真子集。如果(u,v)∈E,且u∈U,v∈V-U,且在所有这样的边中，(u,v)的权c[u][v]最小，那么一定存在G的一棵最小生成树。
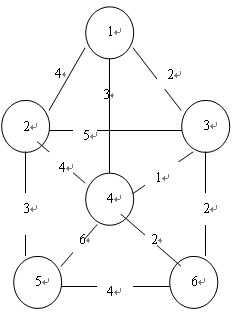
下面给出模板,根据这个图说一下

void Prim(){
	int i,j,k,tmp,ans;
	for(i=1;i<=n;i++)
	dis[i]=inf;//把每个点的距离都初始化
	dis[1]=0;//以第一个点作为起点
	for(i=1;i<=n;i++){//从第一个节点开始
		tmp=inf;//初始化临时距离
		//
		for(j=1;j<=n;j++){
			if(!vis[j]&&tmp>dis[j]){
				tmp=dis[j];
				k=j;
			}//找出最小距离的节点 
		}
		ans+=tmp;
		vis[k]=1;//把访问的节点做标记+
		for(j=1;j<=n;j++){
			if(!vis[j]&&dis[j]>map[k][j])//查找一下以k为起点周围点的距离
			dis[j]=map[k][j];//更新最短距离 
		}
	}

dis[1]=0,ans=0,更新dis[3]=2
dis[3]=2,ans=2,更新dis[4]=1
dis[4]=1,ans=3,更新dis[6]=2
dis[6]=2,ans=5,更新dis[5]=4
dis[5]=4,ans=9,更新dis[2]=3
dis[2]=3,ans=12，无法更新了
输出12

下面给出一个例题洛谷p1265
题目描述
某国有n个城市，它们互相之间没有公路相通，因此交通十分不便。为解决这一“行路难”的问题，政府决定修建公路。修建公路的任务由各城市共同完成。

修建工程分若干轮完成。在每一轮中，每个城市选择一个与它最近的城市，申请修建通往该城市的公路。政府负责审批这些申请以决定是否同意修建。

政府审批的规则如下：

（1）如果两个或以上城市申请修建同一条公路，则让它们共同修建；

（2）如果三个或以上的城市申请修建的公路成环。如下图，A申请修建公路AB，B申请修建公路BC，C申请修建公路CA。则政府将否决其中最短的一条公路的修建申请；

（3）其他情况的申请一律同意。

一轮修建结束后，可能会有若干城市可以通过公路直接或间接相连。这些可以互相：连通的城市即组成“城市联盟”。在下一轮修建中，每个“城市联盟”将被看作一个城市，发挥一个城市的作用。

当所有城市被组合成一个“城市联盟”时，修建工程也就完成了。

你的任务是根据城市的分布和前面讲到的规则，计算出将要修建的公路总长度。

输入输出格式
输入格式：
第一行一个整数n，表示城市的数量。(n≤5000)

以下n行，每行两个整数x和y，表示一个城市的坐标。(-1000000≤x，y≤1000000)

输出格式：
一个实数，四舍五入保留两位小数，表示公路总长。（保证有惟一解）

输入输出样例
输入样例#1： 复制
4
0 0
1 2
-1 2
0 4
输出样例#1： 复制
6.47

思路:看着这个空间范围就知道邻接矩阵会炸，那么用的时候再算就行，然后就是一个洛的prim

#include<iostream>
#include<stdio.h>
#include<cmath>
#include<algorithm>
using namespace std;
#define MAXN 20+5
double dis[5000];
int vis[5000];
struct node{
    double x;double y;
}a[5000];
double cal(int m, int n) {
    return sqrt((double)(a[m].x - a[n].x) * (a[m].x - a[n].x) + (double)(a[m].y - a[n].y) * (a[m].y - a[n].y));
}
double tmp,ans;
int n;
int k;
int main()
{cin>>n;
for(int i=1;i<=n;i++)
cin>>a[i].x>>a[i].y;
    for(int i=1;i<=n;i++)
    dis[i]=999999;//初始化 
    dis[1]=0;
    k=1;
    for(int i=1;i<=n;i++){
        tmp=999999;
        for(int j=1;j<=n;j++){
            if(!vis[j]&&tmp>dis[j]){
                tmp=dis[j];
                k=j;
            }//找出最小距离的节点 
        }
        ans+=tmp;
        vis[k]=1;//把访问的节点做标记+
        for(int j=1;j<=n;j++){
            if(!vis[j]&&dis[j]>cal(k,j))
            dis[j]=cal(k,j);//更新最短距离 
        }
    }
        printf("%.2lf",ans);
        return 0;
    
    }