本原元（维基百科，自由的百科全书）

最新推荐文章于 2021-01-12 15:14:05 发布

转载最新推荐文章于 2021-01-12 15:14:05 发布 · 6.8k 阅读

密码学专栏收录该内容

4 篇文章

订阅专栏

部署运行你感兴趣的模型镜像

原根

在数论，特别是整除理论中，原根是一个很重要的概念。

对于两个正整数 $(a, m) = 1$ ，由欧拉定理可知，存在正整数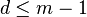 $d /le m-1$ ，比如说欧拉函数 $d = φ(m)$ ，即小于等于 m 的正整数中与 m 互质的正整数的个数，使得 $a^d /equiv 1 /pmod{m}$ 。

由此，在 $(a, m) = 1$ 时，定义 $a$ 对模 $m$ 的指数 $O r d m (a)$ 为使 $a^d /equiv 1 /pmod{m}$ 成立的最小的正整数 $d$ 。由前知 $O r d m (a)$ 一定小于等于 $φ(m)$ ，若 $O r d m (a) = φ(m)$ ，则称 $a$ 是模 $m$ 的原根。

例子

设 $m = 7$ ，则 $/varphi (m)$ 等于6。

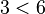设 $a = 2$ ，由于 $2^3 = 8 /equiv 1 /pmod{7}$ ，而 $/displaystyle 3 < 6$ ，所以 2 不是模 7 的一个原根。
设 $a = 3$ ，由于 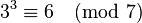$3^1 /equiv 3 /pmod{7}$ ， $3^2 /equiv 2 /pmod{7}$ ， $3^3 /equiv 6 /pmod{7}$ ， $3^4 /equiv 4 /pmod{7}$ ， $3^5 /equiv 5 /pmod{7}$ ， $3^6 /equiv 1 /pmod{7}$ ，因此有 $Ord_7(3) = 6 =/varphi (7)$ ，所以 3 是模 7 的一个原根。

性质

可以证明，如果正整数 $(a, m) = 1$ 和正整数 d 满足 $a^d /equiv 1 /pmod{m}$ ，则 d 整除 $φ(m)$ 。因此 $O r d m (a)$ 整除 $φ(m)$ 。在例子中，当 $a = 3$ 时，我们仅需要验证 3 的 1 、2、3 和 6 次方模 7 的余数即可。

记 $δ = O r d m (a)$ ，则 $a^0,a^1,a^2 /cdots , a^{/delta -1}$ 模 m 两两不同余。因此当 $a$ 是模 $m$ 的原根时， $a^0,a^1,a^2 /cdots , a^{/delta -1}$ 构成模 m 的简化剩余系。

模 $m$ 有原根的充要条件是 $m = 1,2,4, p n,2 p n$ ，其中 $p$ 是奇质数， $n$ 是任意正整数。

对正整数 $(a, m) = 1$ ，如果 a 是模 m 的原根，那么 a 是整数模n乘法群（即加法群 Z/mZ 的可逆元，也就是所有与 m 互素的正整数构成的等价类构成的乘法群）Z_n^×的一个生成元。由于Z_n^×有 $φ(m)$ 个元素，而它的生成元的个数就是它的可逆元个数，即 $φ(φ(m))$ 个，因此当模 $m$ 有原根时，它有 $φ(φ(m))$ 个原根。