数据驱动模型在房产批量估价中的比较

数据驱动技术用于批量评估。在意大利巴里市住宅市场的应用

摘要

由于银行资产负债表中出现不良贷款，全球房地产金融领域发生的一系列事件使得建立能够对不同市场细分的房地产进行“精简”且可靠的批量评估的评估模型成为强制性需求。据意大利银行业协会估计，2014年意大利的不良贷款总额约为3000亿欧元。本文将三种数据驱动技术（享乐价格模型、人工神经网络和进化多项式回归）应用于意大利巴里市某区域最近出售的住宅公寓样本，以检验它们在批量估价中的各自表现。通过统计准确性、结果的实证符合性以及函数关系的复杂性三个方面，对这三种方法所构建的模型进行了比较。

关键词 : 数据驱动技术；享乐价格模型；人工神经网络；ANN；进化多项式回归；市场价值；批量估价。

1 引言

提供“精简的”且可靠的批量估价工具的需求，源于过去十年影响美国及大多数欧盟国家的严重经济和金融危机。这场危机由作为贷款担保的房地产价格下跌所引发，这些房产在借款人违约后的出售时点显示出真实的市场价格，导致银行无法收回所借出的资本。这一问题既源于未及时更新房地产的市场价值以反映实际价格走势，也源于用于确定市场价值的方法不充分，这些方法大多通过单点直接估算来确定，不仅处理周期长，而且得出的结果存在显著偏差。

在欧洲，随着巴塞尔协议II的实施，对贷款担保房地产的评估关注度显著提高，并且在2014年欧洲中央银行引入资产质量审查以检验银行集团稳健性的实践中得到进一步确认。

批量估价技术对于公共和私人不动产资产的管理与提升政策的制定也具有战略性意义，特别是在进行技术与经济再功能化（能源、环境等）投资以及处置不再适用于公共需求的建筑（军营、医院、废弃区域等）时。

在此背景下，批量估价技术的应用占据主导地位。这些方法需要在适当的空间与时间范围内，以系统化方式收集与待评估资产相似的大量房地产样本，并通过统计与数学推导算法进行运算。边界条件的持续变化使得有必要使用能够基于有限数据进行操作、自动捕捉解释变量与价格之间因果关系，并能在短期内预测房产价值的精简模型。

人工神经网络（ANN）满足这些先决条件。许多研究（Brunson 等，1994；McCluskey 等，1997；Wong 等，2002；刘等，2006；Selim，2009）指出：ANN 在预测市场价值方面表现出色，即使在数据有限的情况下也是如此；它们避免了其他模型（例如享乐价格）典型存在的多重共线性、异方差性和空间自相关等计量经济学问题；在解释变量的测量方式上，ANN 对模型设定错误更具鲁棒性。

然而，ANN模型存在一些弱点（杜和古德尼茨基，1993）。首先，神经网络的结构（例如模型输入、传递函数、隐藏层数量等）需要外部预先定义。此外，在参数估计中经常出现过拟合问题。另一个缺点是在学习过程中无法融入已知的经济规律。

在这些方面，已通过遗传编程（GP）取得了一些进展，GP 是一种人工智能方法，能够生成系统模型的结构性表示。GP 最常用的方法称为符号回归，它利用类似于自然界中进化过程的操作，通过一组数据点拟合出数学表达式（Koza，1992）。

多位作者借鉴了遗传算法的逻辑，以改进数学方法在房地产市场中的应用。其中，Król 等（2008）开发了一种模糊规则系统，用于辅助房地产估价，并采用进化算法生成规则库。Wang（2005）构建了一个决策支持系统，通过数据包络分析将数值数据转化为可用于评估房地产投资的信息。Dzeng 和 Lee（2007）提出了一种模型，利用多倍体遗传算法优化度假项目的开发进度。

最近，在土木工程的一些领域实施了一种称为进化多项式回归（EPR）的混合数据驱动技术，该技术结合了遗传规划的有效性与经典数值回归的优势（贝拉尔迪等人，2008；瓦萨洛等人，2016；莫拉诺等人，2015）。该方法的一个高级版本称为EPR‐MOGA，它使用多目标遗传算法来搜索那些同时最大化数据准确性和数学函数简洁性的模型表达式。该方法生成一组针对实验数据具有不同精度和结构模型复杂度的显式表达式。通过分析所生成的表达式，可以选择出最优解。

本文将经典的批量估价数据驱动技术——特征价格（HP）方法与人工神经网络（ANN）方法以及基于EPR‐MOGA的进化方法进行比较，用于构建房地产市场价值的评估模型。在相同的数据库基础上，并针对住宅公寓单价的相同解释变量，分别建立了三种估算模型：一种采用HP方法，一种基于ANN，另一种使用EPR，以检验各自模型的性能。

本文结构如下：第2节阐述了文献中批量估价技术的主要应用；第3节介绍了 HP、ANN和EPR‐MOGA理论的相关内容；第4节引入了案例研究，该研究涉及意大利巴里市房地产市场中最近出售的一组住宅公寓样本。随后，设定了HP、ANN和EPR‐MOGA模型，进行了计算，并对结果进行了比较和说明。第5节讨论了本研究的结论。

2 背景

批量估价技术的潜力在国际文献中的众多应用中得到了体现。除了用于税务用途的房产价值估算外，批量估价技术主要被应用于评估房地产价格中位置、生产、技术和经济社会组成部分的权重，以提供一种监测公共和私人投资者决策不确定性的工具，并支持公共管理部门的规划决策。

参考这些目标，可将这些技术分类如下：

• HP方法 ：主要用于量化以下因素对房产价值的影响：社会和城市因素（Emerson，1972年；Mieszkowski和Saper，1978；Blomquist和Worley，1981；Graves等人，1988年；Adair等人，2000；Fletcher等人，2000；Janssen等人，2001；Morancho，2003；Jim和Chen，2006年；Brander和Koetse，2011；Del Giudice和De Paola，2014年；Guarnaccia，2013）；区位因素（Hickman等人，1984年；Guntermann和Colwell，1983年；Colwell等人，1985；Des Rosiers等人，1996；Waddell等人，1993；Walden，1990；Smith，1993；Manganelli等人，2013）；环境因素（Netusil，2013；Crompton，2001；Lutzenhiser和Netusil，2001；Bowes和Ihlanfeldt，2001；Doglioni和Simeone，2014年）；心理因素，例如由邻近建筑重建引起的价值变化（Ding等人，2000）；经济因素，例如与居民收入相关的因素（Taltavull de la Paz，2003；Potepan，1996；Gibler等人，2014；Kryvobokov，2007）

• 人工神经网络 : 主要用于房产价值的预测（博斯特，1991；柯林斯和埃文斯，1994；沃扎拉等，1995；博尼松和奇瑟姆，1997；麦克格雷尔等，1998；切钦等，2000；刘等，2006）以及市场细分（考科等，2002；杜和古德尼茨基，1993；伊斯兰和阿萨姆，2009）

• 空间分析方法 ：通过GIS应用确保权重，房产价格、变量“可达性”（安瑟林和盖蒂斯，1992；格里菲斯，1993；张和格里菲斯，1993；莱文，1996）以及区域发展投资的空间分布评估（斯科尔扎，2013）

• 模糊逻辑方法 ：用于评估土地价值与假设的未来城市发展之间的相关性，将模糊集理论与多目标规划方法相结合（伯恩，1994；巴尼奥利和史密斯，1998；毛和吴，2011；张和高，2013）

• 自回归积分滑动平均（ARIMA）模型 ：用于解释住宅房产价格作为宏观经济变量的函数，例如实际国内生产总值、住房抵押贷款银行融资比率、通货膨胀、失业率等（陈等，2010；埃尔博恩，2008；伊亚科维耶洛，2004；西维塔尼德斯等，2001；金欣和卡莱罗·库尔沃，1999；瓜尔纳恰等，2014）。

这些程序的使用受限于是否有与待评估资产相似的房地产数据可供获取。特别是，这些数据包括销售价格、租金价格以及在特定市场细分中影响房产价值形成的参数的定性和定量信息。

3 HP、人工神经网络和EPR模型概述

HP模型的目的是根据房产的特征来估算其价格（罗森，1974）。理论上，为整个房产支付的价格可以分解为该房产中各个属性的享乐价格。所得的回归系数提供了对单个房产特征价值的估计。这些特征的价格是隐含的，因为只有资产的总价格在实际交易中被明确体现并可观察到。根据享乐主义原则的假设，资产可分解出的各特征的数量有助于确定显性价格（林德，1973）。

人工神经网络是复杂系统（林桑邦猜等，2004），由一组以适当方式组合的基本单元（神经元）构成，形成具有高度互连性的层状网络结构。

神经网络的结构复杂性取决于神经元的数量以及现有连接的数量。根据神经元在网络中所处的层级，可以对其进行分类。第一层称为输入层，由包含外生信息的神经元组成，这些信息被转化为对上层神经元的脉冲信号。与输入层相对的是输出层，其神经元返回网络运行所产生的结果。在这两层之间，可能存在一个或多个由隐藏神经元或隐藏层组成的中间层，负责处理来自输入层的信息并将其转化为输出。

在人工神经网络中，训练由结构的唯一可变部分负责，即连接的权重。通过学习规则调整连接的权重，神经网络能够从反复输入的输入/输出示例对（训练集）中学习特定功能。

神经元之间的信息传递通过激活函数进行，该函数与每个神经元相关联，并且几乎总是模型中所有节点共用的。

为了让神经网络能够学习分配的特定任务，必须向系统传递一种学习技术，即通过该规则可以适当更新网络连接的权重。

最常使用的学习规则是back-propagation方法。该规则允许根据误差（即网络实际输出与目标值之间不时出现的差异）迭代地调整网络连接的权重。

EPR方法可以被视为原始逐步回归的一种推广，该方法相对于回归参数是线性的，但在模型结构上是非线性的。以下方程概括了可在EPR中实现的通用非线性模型结构：

$$
Y = a_0 + \sum_{i=1}^{n} \left[ a_i \cdot \prod_{j=1}^{2^j} f(X_j)^{(i,l)} \right]
$$

其中n为加性项的数量，ai为待确定的数值参数，Xi为候选解释变量，(i, l)—其中l =(1,…,2j)—是方程中第ith项内第lth个输入的指数，f是由用户从一组可能的数学表达式中选择的函数。指数(i, l)也由用户从一组候选值（实数）中选择。

通过基于种群的策略，对模型数学结构进行迭代研究，该策略通过探索方程中各候选输入所对应的指数组合来实现，并采用遗传算法，其中个体由用户选择的方程中的指数集构成。

EPR 所依据的算法不需要对外生定义数学表达式和拟合所收集数据的最佳参数数量进行预设，因为正是遗传算法的迭代过程返回了最佳解决方案。

通过决定系数(COD)检查EPR返回的每个方程的准确性，其定义为：

$$
COD = 1 - \frac{\sum_{i=1}^{N}(y_{\text{detected}} - y_{\text{EPR}})^2}{\sum_{i=1}^{N}(y_{\text{detected}} - y_{\text{mean}})^2}
$$

其中，yEPR为EPR模型估计的因变量值，ydetected为收集到的因变量实际值，N为分析中的样本量。当决定系数接近于1时，模型的拟合效果更好。

一种近期的EPR版本，称为EPR‐MOGA（朱斯托利西和萨维奇，2009年），采用基于帕累托支配准则的进化多目标遗传算法作为优化策略。这些目标相互冲突，旨在：

1. 通过满足适当的方程验证统计标准，以最大化模型精度
2. 通过最小化方程的项数（ai）来最大化模型的简洁性
3. 通过最小化最终方程中解释变量（Xi）的数量来降低模型复杂度。

通过使用微软Office Excel插件函数（EPR MOGA‐XL v.1，可在以下网站免费获取：http://www.hydroinformatics.it），上述基于帕累托支配准则的优化策略能够在建模阶段结束时，针对所考虑的三个目标获得一组模型解（即最优模型的帕累托前沿）。这样，系统可为操作人员提供一系列解决方案，可根据具体需求、对所分析现象的认知以及所用实验数据的类型，从中选择最合适的方案。

4 案例研究

在实地房地产经纪人的协助下，收集了2013–2014年期间意大利巴里市马多内拉区出售的90套住宅房地产样本。该区域的边界已定义为与相应的“微区”一致。根据意大利房地产经纪人的做法，房地产市场按“微区”进行地理划分，这些微区是依据总统令138/1998及财政部随后发布的法规所界定的。根据意大利法规，“微区”是城市区域的一部分，必须在城市规划上同质，同时构成一个同质房地产市场细分。换句话说，微区是房地产市场中的一个区域，其影响房地产价值形成的外在因素（如可达性、服务设施分布、建筑特征、绿地、步行区等）以基本一致的方式演变。

马多内拉区是巴里市的一个中心区域，以19世纪末建造的众多利贝蒂风格建筑以及法西斯时期修建的若干具有文化价值的公共建筑为特征。该区域主要是住宅区，居住人口约1.8万名居民。该区毗邻滨水区，靠近城市的历史中心，并且有多条公交线路，交通十分便利。

在该区域房地产经纪人的协助下，已获得每个住房单元的以下信息：单位售价（PRZ），以房产建筑面积每平方米欧元计；楼层（F），即公寓所在的楼层数；浴室数量（B）；全景视野（P），作为一个定性变量，通过综合评估分为“无”、“足够”和“良好”三类。在模型中，该解释变量设置了两个虚拟变量，分别对应“足够”（Pe）和“良好”（Pg）两种状态；独立供暖（H）情况，采用二分标准表示，若公寓为独立供暖则取值1，集中供暖则取值0；距市中心距离（C），以步行到达市中心所需分钟数表示；公寓的租赁情况（R），采用二分标准表示，若公寓处于出租状态则取值1，否则为0；面积（S），以房产建筑面积的平方米数表示。

由于所研究细分市场中市场价值增值的相对机制，其他常见的内在特征已被排除在分析之外。识别样本中建筑单元之间的等同条件，并未有助于解释市场价值。

表1 提供了在马多内拉区收集的样本中定量变量的统计信息：连续变量（单位售价、距市中心距离、面积）、离散变量（公寓所在楼层、浴室数量）以及虚拟变量（全景视野、独立供暖、租赁情况）。

表1 所收集样本的描述性统计摘要

变量	Mean	偏标差准	区层级/频率
单位售价 [€/m²]	2,764.30	433.80	—
楼层 [n.]	2.97	1.23	0: 0.02, 1: 0.12, 2: 0.14, 3: 0.39, 4: 0.23, 5: 0.10
浴室数量 [n.]	1.66	0.56	1: 0.38, 2: 0.57, 3: 0.05
全景视野	—	—	None: 0.22, 足够: 0.23, Good: 0.55
独立供暖 （1 – 独立，0 – 集中）	0.42	0.51	0: 0.58, 1: 0.42
距市中心距离 [分钟步行]	9.36	4.15	<5: 0.11, 6–10: 0.55, 11–15: 0.07, 16–20: 0.14
租赁情况 （1 – 已出租，0 – 可用）	0.16	0.36	0: 0.85, 1: 0.15
楼层面积 [m²]	88.92	34.87	<50: 0.11, 51–70: 0.23, 71–90: 0.29, 91–110: 0.08, >110: 0.29

4.1 HP模型

关于所采用模型的函数形式选择，根据当前文献中常见的数学表达式（弗莱彻等人，2000；克里沃博科夫，2007年；威廉姆等人，2002），本研究采用了对数线性模型：该模型在系数上是线性的，并将房屋建筑面积单价（以欧元每平方米表示）的自然对数作为响应变量。经验证据表明，解释单价有助于提高模型的拟合效果（卡塞尔和门德尔松，1985）。

本文考虑的HP模型具有以下形式：

$$
\ln Y = \alpha + \beta X + \varepsilon
$$

其中Y为响应变量，α表示模型截距，β为待估计参数向量，X =(X1,…,Xn)为解释变量向量，ε为随机误差和随机扰动项向量，其服从均值为零、方差为σ²的正态分布。

在表2中，总结了HP模型应用的统计结果。

表2 HP模型实施的主要结果

变量	系数	显著性
常数	8.12579	***
F	0.01013	**
B	0.01103	**
Pe	0.00389	*
Pg	0.00155	*
H	0.06179	***
C	–0.02949	***
R	–0.01536	**
S	–0.000137	*

注：‘***’ 表示 < 0.01，‘**’ 表示 < 0.05，‘*’ 表示 <0.15。

所有结果均表明HP模型具有较高的可靠性。解释变量的系数符号和量级与所研究现象的评价性解释一致，这取决于变量的测量方法。单位售价随着楼层、浴室数量、全景视野的增加以及独立供暖的存在而上升，这由各自的正号表明；而随着距市中心距离、租赁情况以及公寓面积的增加，单位售价则下降，这些变量具有负号。

HP模型的决定系数等于0.9333。Student’s t检验对各个解释变量的显著性进行分析，结果表明所有变量均参与了价格的解释，但全景视野和面积的贡献并不十分显著。在95%的置信水平下进行的F-Fisher检验，导致拒绝回归系数向量为零的假设。回归方程设定误差检验报告了可能存在的设定错误。

所采用函数的设定、关于不存在异方差性的White检验，以及验证结构突变存在的Chow检验，其所有p值均高于0.05，表明模型具有可靠性。方差膨胀因子(VIF)的值均低于5，说明自变量之间不存在共线性。所定义模型的均方根误差(RMSE)值为3.4538。平均绝对百分比误差(MAPE)，即原始样本价格与通过HP模型估计值之间的平均百分比误差，等于4.859。最大绝对百分比误差(MaxAPE)，即原始样本价格与HP模型估计值之间的最大百分比误差，为13.0642。

每个变量边际价格的定量确定，即对单位售价形成所产生的相对权重，是HP方法的主要优势之一。特别是，半对数模型的系数具有简单的解释：根据多位作者（Halvorsen和Palmquist，1980年；Giles，2011）的研究，对于非二分变量，其系数乘以100可直接提供解释变量变化所引起的因变量的百分比变化；而对于二分变量，因变量的百分比效应可通过关系式Δpboj= 100 · (e^βj – 1)获得，其中βj为虚拟变量jth的系数。因此，表3中所示的百分比变化是针对所实施的HP模型计算得出的。

表3 HP模型的百分比变化

变量	系数	百分比效应 [%]
常数	8.12579	–
F	0.01013	1.01326
B	0.01103	1.10265
Pe	0.00389	0.382872
Pg	0.00155	0.155342
H	0.06179	6.1798
C	–0.02949	–2.949
R	–0.01536	–1.5356
S	–0.000137	–0.01368

表3显示了HP模型的以下结果：公寓每增加一个楼层或每增加一个浴室，价格将增加约1.00%。其相应影响范围从0%（底层）到5.07%（第五层），以及从1.10%（一个浴室）到3.31%（三个浴室）；两个考虑的二分变量所估计出的隐含价格及其数值的不一致性进一步证实了全景视野的影响有限，因为‘足够’类别（= 0.38 %）的影响高于‘良好’类别（= 0.15%）的影响；独立供暖的存在使单价增加了6.18%；步行至中心每多花费一分钟，单价将减少–2.949%。此项减少的影响范围分别为11.796%至58.98%，对应步行时间约为4分钟和约20分钟；租赁情况对价格的影响仅为1.54%；最后，面积的影响非常小，对于120平方米的公寓，最大降幅为1.64%。

4.2 ANN模型

要指定ANN模型，必须定义网络拓扑（隐藏层数量及每层中的神经元数量）、传播规则、激活函数和学习规则。

这里采用了multi-layer perceptron网络，其包含一个隐藏层（十三个节点）、一个包含八个外生变量的输入层，以及一个以实际单价的自然对数为输出的输出层。假设采用一个全连接前馈网络，这意味着激活信号从输入层单向传递到输出层，并且每一层中的单元都与下一层中的所有其他单元相连。

在输入层和输出层，每个神经元都关联一个S型激活函数，该函数使用以下解析表达式在0到1之间连续建模：

$$
f(x) = \frac{1}{1 + e^{-kx}}
$$

其中x是输入，k是曲线在拐点处切线的斜率。

尝试了多种替代拓扑结构，包括具有两层和三层隐藏层的结构，以及不同数量的神经元和激活函数。然而，最佳结果是通过将要介绍的ANN模型获得的。

该模型通过使用“BKP－神经网络模拟器”软件（巴里莱等人，1999年）实现，该软件采用反向传播（BKP）算法来迭代调整连接权重。

根据标准分析实践，估计样本已随机分为两组：“训练集”和“测试集”。训练集包含样本的80%，对应72笔交易，剩余18个案例作为测试集。

在所使用的软件中，采用了随机起始点，主要训练参数的值如下：斜率k项 = 1；学习率= 0.65；动量项= 0.1；最大迭代次数= 25,000。

选择的误差函数为均方根误差（RMSE）。所定义的模型对应的RMSE值为1.2623。确定性指数（R²）等于0.9932。平均绝对百分比误差（MAPE），即原始样本价格与人工神经网络估计值之间的平均百分比误差，为3.9155。最大绝对百分比误差（MaxAPE），即原始样本价格与ANN模型估计值之间的最大百分比误差，为10.0744。

敏感性分析（表4）允许通过误差比来评估每个外生变量的影响，该误差比是通过比较剔除待分析解释变量后模型的均方根误差与包含所有变量的模型的均方根误差得到的。

表4 ANN模型的敏感性分析

变量	比率	重要性顺序
C	2.016161	1
H	1.596292	2
F	1.509742	3
Pg	1.487650	4
R	1.354432	5
S	1.349758	6
Pe	1.298589	7
B	1.222877	8

需要注意的是，使用人工神经网络时，变量的重要性按降序排列如下：到市中心的距离（C）、独立供暖（H）的存在、楼层（F）、“良好”的全景视野（Pg）、租赁情况（R）、公寓的面积（S）、“足够”的全景视野（Pe），最后是房产的浴室数量（B）。

4.3 EPR模型

方程中报告的基本模型结构在未选择任何函数f的情况下使用，每个加性单项式项被假定为输入（即解释变量）以其相应指数的幂次组合而成。候选指数属于集合 (0; ‐1; 1)，以便于解释生成的结果，并表示候选输入与因变量之间的正/反比关系。

最终表达式中加性项的最大数量n设定为八，等于所考虑的解释变量的数量。

在这些条件下，EPR‐MOGA软件的运行得到了十二个模型（Mi），如表5所示，这些模型具有不同数量的加性项和解释变量，以及在决定系数（COD）方面表现出的不同精度（图1）。

表5 通过实施EPR‐MOGA获得的方程

M1
$$
\ln(\text{PRZ}) = 8.2664 - 0.0379C
$$

M2
$$
\ln(\text{PRZ}) = 8.2046 + 0.0339C + 0.0574H
$$

M3
$$
\ln(\text{PRZ}) = 8.1536 + 0.03159C + 0.0563H + 0.01F
$$

M4
$$
\ln(\text{PRZ}) = 8.1905 - 0.0325C + 0.3561\frac{H}{C}
$$

M5
$$
\ln(\text{PRZ}) = 8.1641 - 0.0295C + 0.0711H - 0.4403R - 0.0284CR
$$

M6
$$
\ln(\text{PRZ}) = 8.1139 - 0.0243C + 0.4705R + 0.0322CR - 0.5132\frac{H}{C}
$$

M7
$$
\ln(\text{PRZ}) = 8.0293 - 0.0258C + 0.3784R + 0.0344B + 0.0247H - 0.5147\frac{F}{C} + 0.0022B
$$

M8
$$
\ln(\text{PRZ}) = 8.1398 - 0.0266C + 0.5637R + 0.1025B - 0.0314\frac{H}{C} + 0.545\frac{F}{C} - 0.0034\frac{B}{C} - 0.0508\frac{R}{F}
$$

M9
$$
\ln(\text{PRZ}) = 8.096 - 0.0299C + 0.3860R + 0.0232B + 0.5324\frac{H}{C} + 0.0039\frac{F}{C} + 5.9505\frac{R}{F} - 0.02\frac{B}{C}
$$

M10
$$
\ln(\text{PRZ}) = 8.0916 - 0.0234C + 0.5066R + 0.0456H + 0.0341P_g - 0.2252\frac{H}{C} + 3.7734\frac{P_g}{H} - 1.2658\frac{B}{S}
$$

M11
$$
\ln(\text{PRZ}) = 8.1135 - 0.0249C + 0.4646R - 0.0312CR + 0.2671P_g + 2.4002\frac{H}{C} - 1.1754\frac{P_g}{H} + \frac{B}{S}
$$

M12
$$
\ln(\text{PRZ}) = 8.1041 - 0.0244C + 0.475R - 0.0318CR + 0.3073P_g + 1.5295\frac{F}{P_g} + 0.9643\frac{H}{B} - \frac{S}{B}
$$

对模型的考察表明，从模型M4开始，软件生成的数学表达式变得复杂，因为相同的解释变量出现在模型的多个项中，并且还与其他变量组合。这种情况虽然可能得到能更好拟合价格的函数，但另一方面也产生了复杂的表达式，使得对现象的解释变得困难。

EPR‐MOGA 得到的模型的决定系数始终接近于1，其范围从对应于模型 M1 的最小值91.43%到对应于模型 M10 的最大值96.29%（图1）。

然而，在模型M3（其决定系数COD为93.69%）之后，准确性的提升变得相对显著。特别是对于模型M4、M9和M11，除了决定系数COD降低外，还应强调其数学函数复杂性的明显增加，相较于紧邻的前一个模型而言。

这些考虑表明，应仅关注软件生成的前三个模型。

从模型M1到模型M3所获得的数学方程的演变过程提供了一些重要信息：第一，涉及主要外生变量在解释观测价格中的重要性，这可通过前三个模型中变量出现的顺序来推断，即距市中心距离（C）、独立供暖（H）的存在以及楼层（F）；第二，相关信息体现在自变量系数符号的经验合理性上，这明确表明了单价（PRZ）与变量距市中心距离（C）之间存在反比关系，而与变量独立供暖（H）的存在和楼层（F）则呈现正比关系；第三，信息表明，变量距市中心距离（C）、独立供暖（H）的存在以及楼层（F）的组合已能较好地解释价格。在M3之后模型的方程中引入其他变量将导致表达式过于复杂，难以用于对现象的解释。

因此，M3 是能够有效解释和再现所分析样本价格形成机制的模型。对于该模型，均方根误差（RMSE）值为1.0723；确定系数（R²）等于0.9998；平均绝对百分比误差（MAPE）为3.3172；最大绝对百分比误差（MaxAPE）为8.8689。

此外，模型 M3 还可用于计算解释变量的边际价格（表6）。

表6 模型M3所选解释变量对单价（PRZ）的百分比效应

变量	系数	百分比效应 [%]
距市中心距离（C）	–0.03159	–3.159
独立供暖（H）	0.0563	5.792
楼层（F）	0.01	1.00

表6显示了以下结果：步行到centre所需时间每增加1分钟，价格就会下降–3.159%。这种减少的影响范围分别为12.636%和63.18%，对应步行时间约为4分钟和约20分钟的情况；独立供暖的存在使单价提高了5.792%；每增加一个楼层，价格就会上涨1.00%。这种上涨的影响范围从0%到5.00%，分别对应底层和第五层。

4.4 模型之间的比较

HP模型、ANN模型和EPR模型的性能，以R², RMSE、平均绝对百分比误差和最大绝对百分比误差计算，总结于表7和图2中。统计指标和图2中的图表表明，所选EPR模型（M3）在评估巴里市马多内拉区房产价格方面具有最高的准确性。

表7 模型性能比较

性能指标	HP模型	ANN模型	EPR模型
R²	0.9333	0.9932	0.9998
RMSE	3.4538	1.2623	1.0723
MAPE	4.859	3.9155	3.3172
最大APE	13.0642	10.0744	8.8689

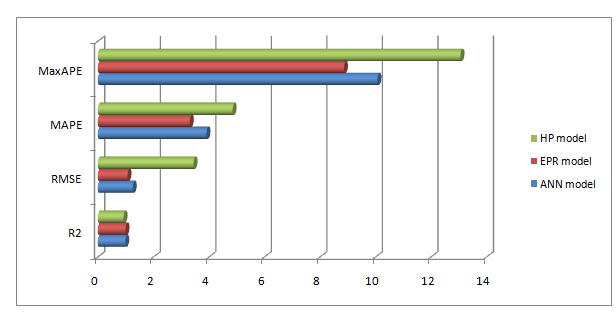
与HP模型相比，HP模型在最终函数中考虑了所有初始解释变量，而EPR模型具有更简洁的数学表达式，同时具备更高的统计准确性。实现EPR‐MOGA所依赖的遗传算法能够识别在所选样本价格形成过程中起主导作用的变量，并精确估计这些变量的“权重”，同时从计算中剔除那些影响结果良好性的较不显著的参数。

这是一个重要的优势，因为即使ANN方法背后复杂的函数形式也无法达到比EPR模型更高的统计准确性。

关于结果的实证解释，值得注意的是，在考虑的三个模型（HP、人工神经网络、EPR‐M3）中，“前三名”的位置相同（距市中心距离、是否存在独立供暖、楼层）。分析证实，在马多内拉区，位置（变量C）是对住宅房产升值影响最大的因素。

在这方面，值得注意的是，由于缺乏其他因素，该变量的重要性被进一步凸显。马多内拉区与巴里市中心的快速连接（如地铁或轻轨）。

独立供暖（H）的存在位列第二。该变量的重要性一方面表达了买家对由独立供暖带来的更高居家舒适度的认可；另一方面也体现了人们希望避免在公寓楼中因供暖问题经常产生的纠纷（内斯蒂科和皮波洛，2015年）：事实上，尽管《意大利共有公寓法》（第220/2012号法律）已简化了脱离集中供暖系统的程序——前提是此类改造不会对集中供暖系统的运行产生额外费用或不便——但其他法规（第59/2009号总统令；第192/2005号法令）要求，欲从集中供暖系统分离的公寓业主必须验证其所安装的独立供暖系统的节能能力。未能遵守这些法规可能引发法律纠纷，这常常成为将集中供暖系统改为公寓独立供暖的障碍。

公寓所在楼层的显著影响 f loor（F）反映了当公寓所在建筑配备电梯时，通常会赋予该特征的重视程度，而所收集样本中的所有公寓均满足这一条件。

初始数据库的其他变量（B, Pe, Pg, R, S）参与了HP模型和ANN模型中的价格形成机制，但未包含在EPR‐M3模型中。特别是，对HP模型和ANN模型进行的分析表明，在这两个模型中，租赁情况（R）、面积（S）以及‘一般’的全景视野（Pe）在解释房产价格方面具有相同的重要性顺序（分别为第5、第6和第7位），而浴室数量（B）和‘良好’的全景视野（Pg）则被以截然相反的方式解释（在HP模型中，B为第4位，Pg为第8位；在ANN模型中，Pg为第4位，B为最后一位）。

ANN模型更高的统计精度使得变量楼层（第3位）与‘良好’的全景视野（在ANN模型中为第4位）之间的经验相关性更加明显；由于HP模型的统计特性，这种相关性表现为该模型在解释现象能力上的减弱，即HP模型赋予‘一般’的全景视野的权重高于‘良好’的全景视野。

所描述的共线性效应也出现在EPR‐MOGA应用所得的方程中，其中楼层水平被视为全景视野的一个“代理”变量。只有“良好”的全景视野变量（Pg）出现在最后三个模型（EPR‐M10、EPR‐M11和EPR‐M12）中，这些模型具有相当复杂的数学表达式，其中变量F和Pg 最终组合成一个唯一的加法项。

5 结论

在意大利房地产行业所处的不确定性阶段，使用创新的评估工具可使市场参与者做出更可靠的估价，并有效监控房产价值的演变。

本文在同一个数据库上，针对住宅市场价格的相同解释变量，实施了三种数据驱动方法。巴里市（意大利）某区域最近出售的公寓：一种通过HP方法，一种基于ANN理论，另一种使用EPR‐MOGA程序并根据结果的准确性和可解释性选择最合适的方程。

最后两种方法在应用中表现出色，但EPR‐M3模型能够在预测市场价格时同时实现最佳的统计准确性，快速检验所得结果的经验一致性，并克服ANN模型的主要局限性。事实上，ANN属于“黑箱”，即无法在输入值和输出值之间建立直接的函数关系，也无法精确地研究和再现价格形成的机制。此外，通过ANN获得的结果可能不稳定，且随着样本量增加才得以改善；甚至使用相同数据但由不同软件包生成的模型结果也可能存在差异。而EPR模型则克服了这些缺点：所获得的数学表达式的透明性使得可以验证（并量化）解释变量在房产价格形成中的显著性。

本文选用的EPR‐M3模型配置为半对数方程，该方程可通过享乐定价法得出，并将EPR‐MOGA识别出的对房产价格最具代表性的三个特征作为自变量。

EPR‐MOGA所基于的遗传算法的优势在于能够自动且快速地选择在准确性和理解性方面最优的回归函数，而这一结果通过HP方法难以实现。因此，这对于房地产估价而言具有重要的附加价值，因为在房地产估价中，必须拥有具备高性能且易于解释的预测函数。

本研究中确定的EPR‐MOGA模型可能具有有趣的应用：事实上，将房地产价格表示为仅三个解释变量（距市中心距离、独立供暖的存在和楼层）以及一个常数加性项的函数，该模型有可能成为意大利地籍册改革（第23/2014号法律）中为位于同一地理微区的房地产分配批量估价功能的一种简单而有效的工具，在此情况下，应获取其位置和两个易于获得的内在特征。