【从零构建大模型】第2课,从零构建简单transformer与带权重transformer、多头注意力
概述
本文总结《从零构建LLM》的笔记,加深对GPT的理解,对QKV的理解。
作者写了做个文章在下面公众号(驾驭AI美未来、大模型生产力指南),目的是提升大模型、智能体的理解,提高大家生产力,欢迎关注、点赞。
录了个视频课程,欢迎学习。
【从零构建大模型】 视频课程讲解,一步步带你理解大模型底层原理
1. 自注意力机制
1.1 构建自注意力机制

1.2 学习思路,分四步,逐步提升难度
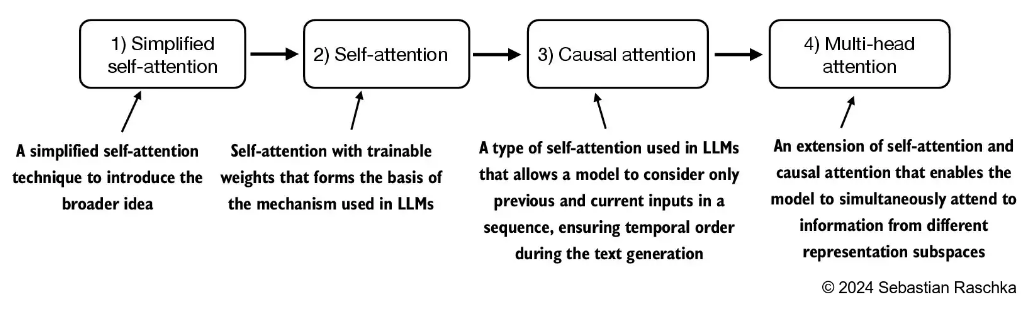
2.1 简化版自注意力机制
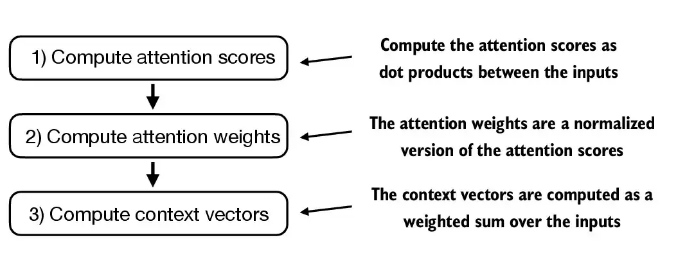
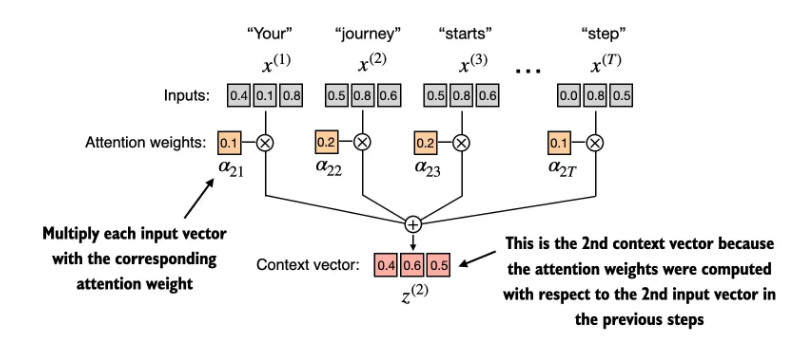
思路:就是下图的3个步骤
数据:是六个数的emdedding,维度是3
import torch
inputs = torch.tensor(
[[0.43, 0.15, 0.89], # Your (x^1)
[0.55, 0.87, 0.66], # journey (x^2)
[0.57, 0.85, 0.64], # starts (x^3)
[0.22, 0.58, 0.33], # with (x^4)
[0.77, 0.25, 0.10], # one (x^5)
[0.05, 0.80, 0.55]] # step (x^6)
)
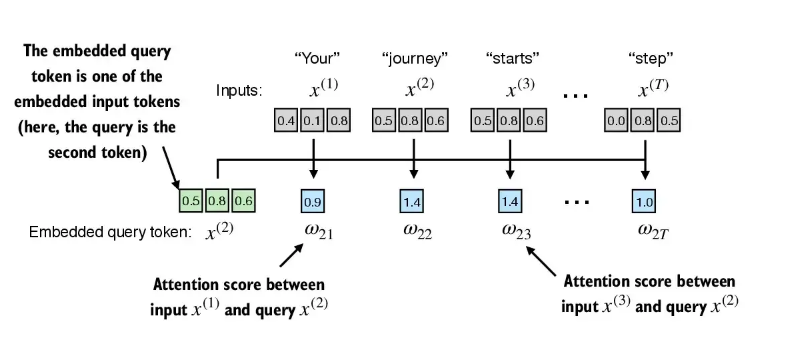
- 第一步: 计算 注意力分数
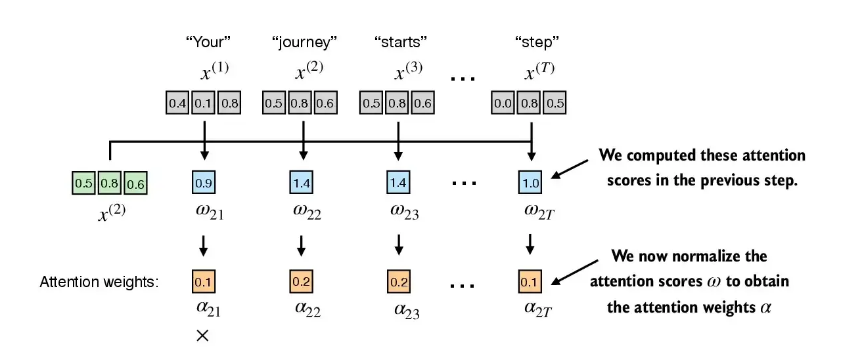
- 第二步:把注意力分数归一化,得到归一化后的权重
- 第3步: 计算context vector
2. 带训练权重的注意力机制
- 目标
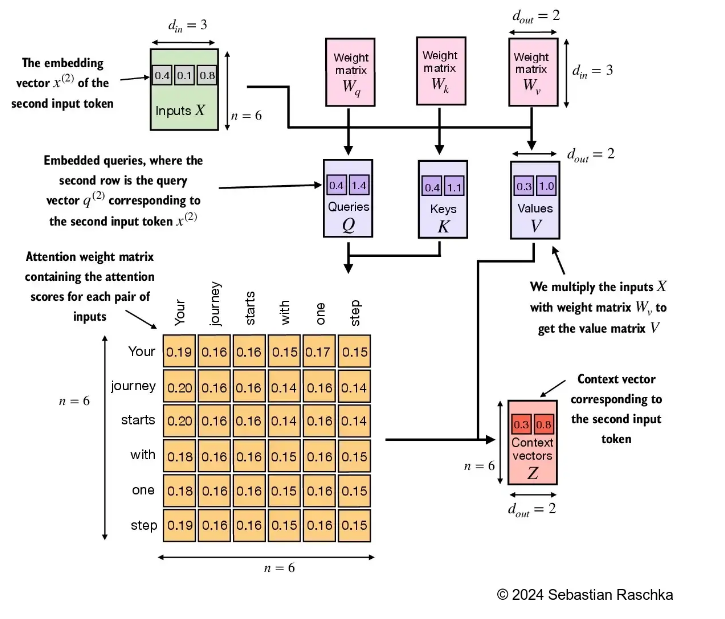
2.1 步骤1,初始化QKV
Transformer 中的 Q、K、V 与词汇表的关联是通过模型的输入处理流程间接建立的,具体关联路径如下:
词汇表与嵌入层的映射词汇表中的每个 token(如单词或子词)首先通过嵌入层(Embedding Layer)映射为固定维度的向量(即词嵌入)。例如,若词汇表大小为V,嵌入维度为d_model,则嵌入层本质是一个V×d_model的矩阵,每个 token 通过索引查表得到对应的d_model维向量。
词嵌入到 Q、K、V 的转换得到的词嵌入(或经过位置编码后)会作为 Transformer 编码器 / 解码器的输入,通过三个独立的线性层(权重矩阵分别为W_Q、W_K、W_V)转换为 Q、K、V:
Q = X × W_Q
K = X × W_K
V = X × W_V
其中X是包含词嵌入信息的输入矩阵(形状为[batch_size, seq_len, d_model]),转换后的 Q、K、V 仍保持d_model维度(或拆分为多头注意力的d_k维度)。
关联的本质:通过输入建立间接联系Q、K、V 的数值源于输入序列的词嵌入,而词嵌入又直接对应词汇表中的 token,因此 Q、K、V 携带了词汇表中 token 的语义信息。但需注意:
Q、K、V 的维度(如d_model)与词汇表大小V无关,仅由模型设计决定;
词汇表的变化(如增减 token)只会影响嵌入层矩阵的大小,不会改变 Q、K、V 的维度或计算逻辑。
简言之,词汇表通过 “token→词嵌入→线性变换” 的链条将语义信息传递给 Q、K、V,但两者在维度设计上相互独立。这种分离设计使模型能灵活调整词汇表(如支持多语言),同时保持注意力机制的稳定性。
代码:
torch.manual_seed(123)
W_query = torch.nn.Parameter(torch.rand(d_in, d_out), requires_grad=False)
W_key = torch.nn.Parameter(torch.rand(d_in, d_out), requires_grad=False)
W_value = torch.nn.Parameter(torch.rand(d_in, d_out), requires_grad=False)
keys = inputs @ W_key
values = inputs @ W_value
querys = inputs @ W_query
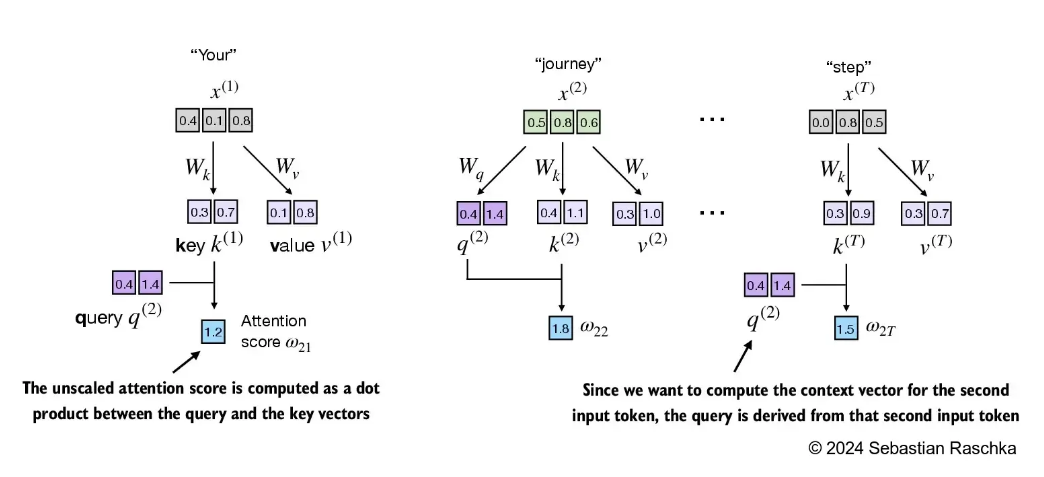
2.2 计算注意力分数
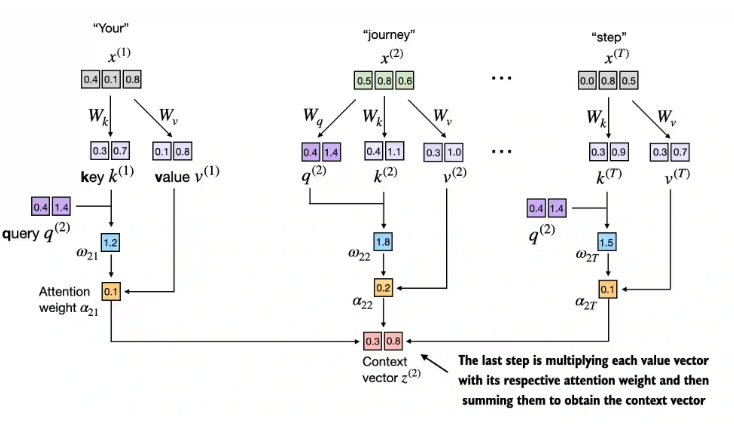
2.5 过程汇总
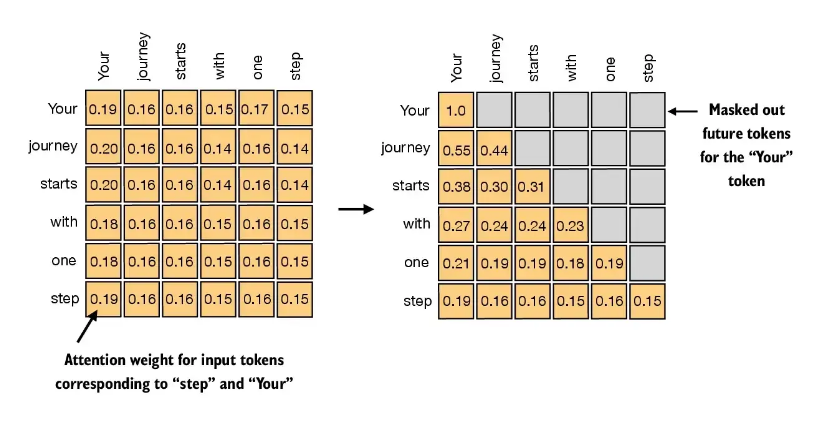
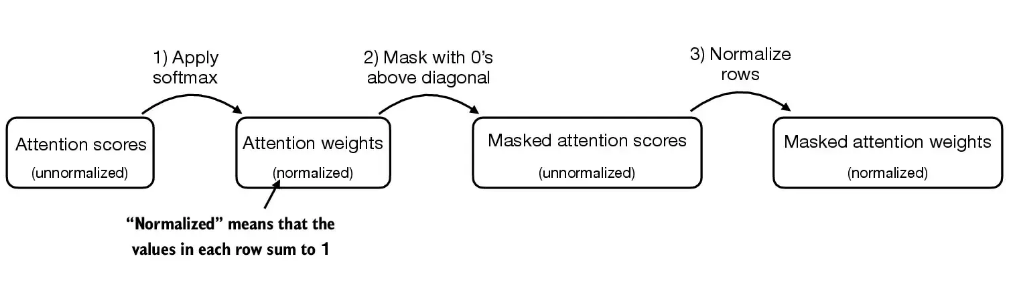
2.6 因果注意力
掩码条矩阵的上半部分
思路:
注意力分数
tensor([[0.1921, 0.1646, 0.1652, 0.1550, 0.1721, 0.1510],
[0.2041, 0.1659, 0.1662, 0.1496, 0.1665, 0.1477],
[0.2036, 0.1659, 0.1662, 0.1498, 0.1664, 0.1480],
[0.1869, 0.1667, 0.1668, 0.1571, 0.1661, 0.1564],
[0.1830, 0.1669, 0.1670, 0.1588, 0.1658, 0.1585],
[0.1935, 0.1663, 0.1666, 0.1542, 0.1666, 0.1529]],
掩码:
tensor([[0.1921, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.2041, 0.1659, 0.0000, 0.0000, 0.0000, 0.0000],
[0.2036, 0.1659, 0.1662, 0.0000, 0.0000, 0.0000],
[0.1869, 0.1667, 0.1668, 0.1571, 0.0000, 0.0000],
[0.1830, 0.1669, 0.1670, 0.1588, 0.1658, 0.0000],
[0.1935, 0.1663, 0.1666, 0.1542, 0.1666, 0.1529]],
grad_fn=<MulBackward0>)
- 归一化
tensor([[1.0000, 0.0000, 0.0000, 0.0000, 0.0000, 0.0000],
[0.5517, 0.4483, 0.0000, 0.0000, 0.0000, 0.0000],
[0.3800, 0.3097, 0.3103, 0.0000, 0.0000, 0.0000],
[0.2758, 0.2460, 0.2462, 0.2319, 0.0000, 0.0000],
[0.2175, 0.1983, 0.1984, 0.1888, 0.1971, 0.0000],
[0.1935, 0.1663, 0.1666, 0.1542, 0.1666, 0.1529]],
- 把对角线上的0全部改为负无穷
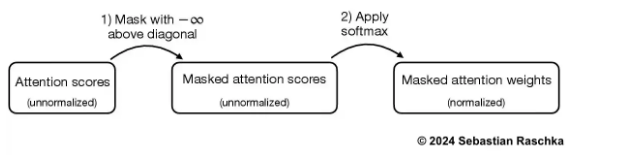
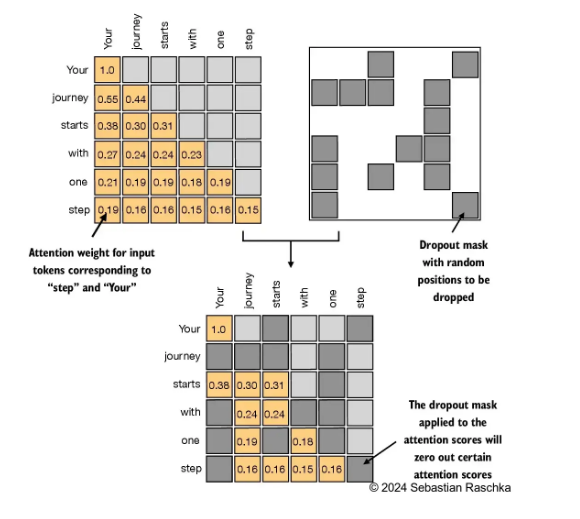
2.7 dropout 减少过拟合
- 因果注意力类
import torch
import torch.nn as nn
# 因果注意力机制类,继承自PyTorch的Module
# 因果注意力机制确保每个位置只能关注到它之前的位置,适用于语言建模等时序任务
class CausalAttention(nn.Module):
# 初始化方法,定义模型的参数和层
# 参数说明:
# - d_in: 输入特征维度
# - d_out: 输出特征维度(同时也是Q、K、V的维度)
# - context_length: 最大上下文长度(序列长度)
# - dropout: dropout概率,用于防止过拟合
# - qkv_bias: 是否在线性层中使用偏置项
def __init__(self, d_in, d_out, context_length,
dropout, qkv_bias=False):
super().__init__() # 调用父类的初始化方法
self.d_out = d_out # 保存输出维度
# 定义三个线性变换层,分别用于计算查询(Query)、键(Key)和值(Value)
self.W_query = nn.Linear(d_in, d_out, bias=qkv_bias)
self.W_key = nn.Linear(d_in, d_out, bias=qkv_bias)
self.W_value = nn.Linear(d_in, d_out, bias=qkv_bias)
self.dropout = nn.Dropout(dropout) # Dropout层,用于注意力权重的正则化
# 注册因果掩码作为缓冲区(不会被视为模型参数,但会随模型一起保存)
# torch.triu生成上三角矩阵,对角线为1,上三角为1,下三角为0
# diagonal=1表示主对角线以上的元素为1
self.register_buffer('mask', torch.triu(
torch.ones(context_length, context_length), diagonal=1)
)
# 前向传播方法,定义数据的流动过程
# 参数x: 输入张量,形状为(batch_size, num_tokens, d_in)
def forward(self, x):
# 获取输入张量的形状信息
# b: 批次大小,num_tokens: 序列中的token数量,d_in: 输入特征维度
b, num_tokens, d_in = x.shape
# 注意:如果num_tokens超过context_length,掩码操作会出错
# 在实际应用中,LLM会确保输入长度不超过context_length
# 通过线性变换计算Q、K、V
# 输出形状均为(batch_size, num_tokens, d_out)
keys = self.W_key(x)
queries = self.W_query(x)
values = self.W_value(x)
# 计算注意力分数:Q和K的点积
# keys.transpose(1, 2)将键的最后两个维度交换,形状变为(b, d_out, num_tokens)
# 点积结果形状为(b, num_tokens, num_tokens)
attn_scores = queries @ keys.transpose(1, 2)
# 应用因果掩码:将未来位置的注意力分数设为负无穷
# 这样在计算softmax时,这些位置的权重会趋近于0
# self.mask.bool()[:num_tokens, :num_tokens]确保掩码大小与实际token数量匹配
attn_scores.masked_fill_(
self.mask.bool()[:num_tokens, :num_tokens], -torch.inf
)
# 计算注意力权重:对注意力分数进行softmax归一化
# 除以keys维度的平方根(d_out**0.5)进行缩放,防止梯度消失
# 在最后一个维度(-1)上进行softmax,确保每个token的注意力权重和为1
attn_weights = torch.softmax(
attn_scores / keys.shape[-1]**0.5, dim=-1
)
# 对注意力权重应用dropout,增强模型泛化能力
attn_weights = self.dropout(attn_weights)
# 计算上下文向量:注意力权重与V的加权和
# 结果形状为(batch_size, num_tokens, d_out)
context_vec = attn_weights @ values
return context_vec
# 设置随机种子,确保实验结果可复现
torch.manual_seed(123)
# 从输入批次中获取实际的上下文长度(序列长度)
context_length = batch.shape[1]
# 创建CausalAttention实例
# 假设d_in和d_out已提前定义,分别为输入和输出维度
# dropout设为0.0表示不使用dropout(可能用于调试或评估阶段)
ca = CausalAttention(d_in, d_out, context_length, 0.0)
# 将批次数据输入到因果注意力模型中,得到上下文向量
context_vecs = ca(batch)
# 打印输出结果和形状,用于验证
print(context_vecs)
print("context_vecs.shape:", context_vecs.shape) # 预期形状: (batch_size, num_tokens, d_out)
2.8 多头注意力
2.8.1 核心思想
核心思想:两个头的为例子: 一个头产生一个 context vector1,(0.7,-0.1) ,第二个头生成(0.7,0.4),把他们拼接就成(0.7,-0.1,0.7. 0.4)
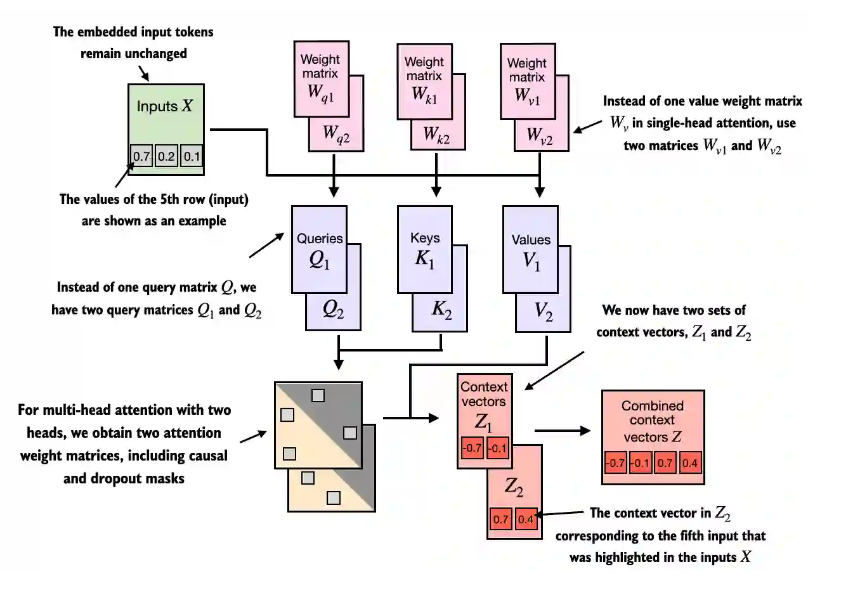
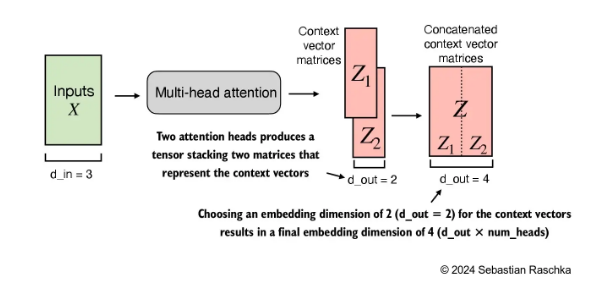
2.8.2 两头与三头的结果值



代码:
class MultiHeadAttentionWrapper(nn.Module):
def __init__(self, d_in, d_out, context_length, dropout, num_heads, qkv_bias=False):
super().__init__()
self.heads = nn.ModuleList(
[CausalAttention(d_in, d_out, context_length, dropout, qkv_bias)
for _ in range(num_heads)]
)
def forward(self, x):
return torch.cat([head(x) for head in self.heads], dim=-1)
torch.manual_seed(123)
context_length = batch.shape[1] # This is the number of tokens
d_in, d_out = 3, 2
mha = MultiHeadAttentionWrapper(
d_in, d_out, context_length, 0.0, num_heads=4
)
context_vecs = mha(batch)
print(context_vecs)
print("context_vecs.shape:", context_vecs.shape)
2.8.3 把向量值合并到一个vectorContexts 里面
























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








