自适应分布式LT码在Y型网络中的应用

将分布式LT码适配到Y型网络：传感器网络中收集树的抽象

1. 引言

无线传感器网络技术的进步使得这些网络能够支持多种应用，例如环境监测 [Mo 等 2009],、安全监控 [He 等 2004],以及定位 [Yang 和 Liu 2010a, 2010b],等。传感器网络在现实世界中的一些部署实例包括用于野外监控的 Vigil‐Net [Vicaire 等 2009],、用于天气监测的 SensorScope [Barrenetxea 等 2008],、用于环境监测的 GreenOrbs [Mo 等 2009],，以及大规模太阳能供电的传感器网络 Trio [Dutta 等 2006]。在没有集中控制的分布式传感器网络中，通常采用汇聚树方案来收集数据 [Gnawali 等，2009； Tan 等 2011]。

该方法将汇聚节点设为树的根节点，传感器通过其他传感器节点以多跳方式与汇聚节点通信。该方法的主要缺点是在具有不可靠链路的有损网络中，由于使用基于ARQ的策略，导致重传次数较多。作为解决方案，文献中已提出多种算法[Cao和Yang 2010；Apavatjrut等 2012；Zhou等 2012]，采用喷泉码方案替代ARQ技术进行错误恢复，以减少反馈消息和重传次数。

喷泉码 [Byers 等人 1998, 2002]是一类最初为二进制删除信道（BEC）设计的前向纠错码。所谓“喷泉”是指发射机持续传输，直到接收机接收到足够数量且无删除的编码符号，从而恢复所有源符号，这类似于从喷泉中接水填满水桶。喷泉码以其所谓的无固定码率特性而闻名，即可以从有限数量的源符号中生成无限数量的编码符号。由于其无固定码率特性，这些码可以即时处理地自适应调整码率，且在设计时无需预先了解BEC的删除率。此外，它们在反馈消息数量方面非常高效，因为在传输结束时仅需接收机发送一条确认消息，表明所有信息符号已成功恢复。这一点相较于其他传统前向纠错码和ARQ技术具有显著优势。

LT码 [Luby 2002]和Raptor码 [Shokrollahi 2006]是喷泉码中两个著名的类别，其中LT码是喷泉码的第一个实际实现。在Luby [2002]和Shokrollahi [2006]的研究中表明，使用LT码和Raptor码时，随着信息块大小的增加，编码开销趋近于零。由于其通用性、无固定码率特性以及接近容量的性能，LT码 [Luby2002]和Raptor码 [Shokrollahi 2006]适用于具有变化信道特性的网络中的点对点和多播数据传输。喷泉码的一些应用包括可扩展视频流 [Bogino et al. 2007],、混合ARQ [Soijanin et al. 2006],以及可靠数据存储 [Dimakis et al. 2006]。此外，Raptor码的系统化版本已被3GPP [3GPP 2015]标准化用于多媒体广播/多播服务。LT码和Raptor码的另一大特点是其低复杂度的编解码操作。对于包含k个源符号的LT码，每个源符号的平均编解码复杂度为O(log(k))量级，而 Raptor码的该复杂度为常数。

在LT码中，源符号和编码符号是长度相同的比特串。为了生成每个编码符号，首先从度分布中采样一个度d，然后均匀地选择d个源符号，并将它们进行异或操作（按位）以形成新的编码符号。LT码的解码是根据置信传播（BP）算法[Luby 2002]进行的。每个编码符号的度所服从的分布在很大程度上影响LT码的解码开销以及编码/解码复杂度性能。该分布被称为LT码的度分布。在Luby [2002]中，提出了鲁棒孤子分布作为实现LT码接近最优性能的合适度分布。

在无线传感器网络（WSNs）中使用汇聚树方案（其中所有传感器节点相同），位于深度i的传感器节点需要作为中继，为位于深度i+ 1（或更深）的传感器节点转发数据，将其发送至深度i −1（或更浅）的节点，并最终传送到汇聚节点（树的根节点）。此类树形方案的基本构建模块是：来自两个或多个不同源节点到汇聚节点的路由共享部分路径。在这种情况下，中间节点通常采用缓存并转发（BnF）方式，但就整体网络吞吐量而言，该方法效率不高。在 Ahlswede的开创性工作中[2000]，网络编码（NC）被引入作为中间节点的一种更优替代技术，以提高网络吞吐量。

其理论极限。Li 等人 [2003] 已证明，在多播场景中，有限符号大小的线性网络编码足以实现最优网络吞吐量，这一结论由最大流最小割定理 [ Bollobas 1979] 提出。在 Chou 等人 [2003] 和 Ho 等人 [2003] 的研究中，随机线性网络编码（RLNC）被引入作为任意网络中网络编码的一种鲁棒框架。使用 RLNC 时，中间节点通过从有限域 GF(q) 中随机选择系数，对收到的编码符号进行线性组合以实现再编码，而在目的地则采用高斯消元法 （GE）算法计算系数矩阵的逆。在目的地和部分路径被两个或多个路由共享的场景中，必须将网络编码技术与 LT码 结合，以在收集树中达到最优吞吐量，并最小化汇聚节点处的解码开销。

本文研究了多个源通过同一中间节点向一个目的地传输的场景。在文献中，这种拓扑结构被称为Y型网络。当源端使用LT码进行编码时，我们的主要目标是在中继节点采用网络编码（NC）而非BnF，以提高总吞吐量。本文的目标是提出一种算法，使得从目的节点的角度来看能够实现标准LT码的特性，从而使得该算法可以在收集树的不同层上重复使用。因此，在中继节点应使用二进制系数进行线性网络编码。这有利于目的节点降低解码复杂度，因为它可以使用置信传播解码器。置信传播解码器的性能（在开销和复杂度方面）依赖于目的节点接收到的编码符号的度分布。因此，该问题的主要难点在于如何在目的节点提供适合置信传播解码器最佳性能的度分布（如鲁棒孤子分布）。

许多算法[Puducheri et al.2007；Sejdinovic et al. 2009；Liau等，2011；Gu等 2014]已被应用于Y型网络，以在目的地获得类孤子分布。通常，在具有有限资源的Y型网络中，在目的地实现鲁棒孤子分布是一个离散优化问题。这是因为中继无法访问源符号，必须利用从源接收到的编码符号生成所需的度分布。在文献[Puducheri等，2007； Sejdinovic等2009],中先前提出的算法，其主要思想是增强源节点的编码，并在中继处执行简单的异或操作，以在目的地实现期望的度分布。这种方法对源节点引入了许多限制 （在同步和分块大小方面）。因此，本文提出的算法的主要目标是消除对源节点的所有限制。这是通过使中继以更智能的方式运行网络编码来实现期望的目的地分布，而无需对源端使用的度分布进行任何更改来完成的。

本文中，我们设计了一种用于如图1所示Y型网络上的分布式LT编码的算法。我们将该算法称为自适应分布式LT（ADLT）编码算法。在ADLT算法中，我们采用了一种称为度分布更新（DDU）的新技术。该技术使得Y型网络中的中继节点能够在目的地维持任意期望的分布（例如，鲁棒孤子），而源端生成的编码符号则是基于使用鲁棒孤子分布的标准 LT码。与先前提出的算法[Puducheri等，2007；Sejdinovic等 2009],不同，ADLT算法能够适应任意数量的源，且各源可具有不同数量的数据块，并与同一个中继节点通信。ADLT算法在编码开销和灵活性方面的改进是以中继节点增加的内存需求和复杂度负载为代价的，因为中继节点承担了该算法的全部复杂性。

2. 相关工作

在本节中，我们回顾了相关文献，包括先前为Y型网络场景提出的算法。在传感器网络的背景下，Apavatjrut等人[2012]研究了将LT码与网络编码相结合以实现传感器网络中可靠的端到端传输的方法。然而，他们用于分布式网络编码的方法与Champel等人[2010]所提出的方法相同。该方法的缺点在于中继节点的响应不是即时处理的，且中继需要大量内存空间，这在典型的传感器节点中可能不可行。Zhou等人[2012]提出了一种混合方案，结合了喷泉码和ARQ方法。他们的最终目标是通过减少每一跳内的延迟来最小化多跳情况下的端到端延迟。在他们提出的方案中，每个节点先传输固定数量的LT编码数据包，然后根据来自目的地的确认信息，继续传输额外的编码数据包，直到成功解码为止。该过程在每一跳中重复执行。

Puducheri等人[2007]是第一篇研究在Y型网络上进行分布式LT编码的文章。在他们的场景中，中继节点仅对从源节点接收到的编码数据包进行异或并转发。因此，目的地接收到的编码数据包的度分布是源节点用于LT码编码的分布的卷积。他们的思路是通过增强源节点处LT码的编码方式，以在目的地实现鲁棒孤子分布（RSD）。为此，他们对RSD进行了反卷积，并将得到的度分布用于源节点的编码。直接对RSD进行反卷积并不能得到一个可接受的概率密度函数（PDF）。因此，Puducheri等人[2007]采用了两个概率密度函数：一个仅包含RSD中的一度和最后一个峰值，另一个则是通过对RSD其余部分进行反卷积获得的。每次传输时，每个源节点基于伯努利试验选择其中一个分布。DLT算法[使得 Puducheri等人 2007]在无损信道且零擦除的情况下完美恢复了RSD。

概率。为了采用DLT算法[Puducheri等人 2007],然而，存在一些严格的要求：(1) 源数量应为2的幂。(2) 所有源的源符号数量应相同。(3) 从源到中继的传输之间应实现完全同步。此外，当源与中继之间的信道删除率不同时，DLT算法的性能会显著下降。

Sejdinovic等人[2009]提出了一个解决DLT在源数量问题上的方案。在SDLT算法中[， Sejdinovic等人 2009],让中继节点随机组合从各个源接收到的编码符号。参与异或操作的编码符号数量根据一种在中继端应用的分布来选择。为了分析度分布的演化过程， Sejdinovic等人[2009]采用了类似于Shokrollahi [2006]所提出的AND‐OR树分析方法。这些分析最终形成了一种线性规划，用于优化中继节点在组合接收数据包时所使用的分布。然而，SDLT算法仍然需要完全同步，并且要求每个源具有相同数量的源符号。此外， SDLT算法通常并不一定优于DLT算法。

Liau 等人[2011]采用了一种不同于 Puducheri 等人 [2007]和 Sejdinovic 等人 [2009]的方法，用于 Y型网络 中的分布式LT编码。Liau 等人[2011]并未追求精确的 RSD，而是旨在实现一种类孤子分布，同时保持类孤子分布的一些关键特性。SLRC算法 [中，Liau 等人 2011]优先在中继处转发一度和二度的编码符号，因为这些度对于启动置信传播解码更为重要。未被转发的编码符号将保存在中继的内存中，以便在后续时刻转发， 当从任一源接收到的编码符号均不为一度或二度时进行转发。通过这种方式，他们的算法在被删除的编码符号方面所受影响小于 Puducheri 等人 [2007]和 Sejdinovic 等人[2009]提出的算法。

Champel 等人[2010]研究了喷泉码与对等网络中网络编码的结合。他们的主要目标是在对等网络中使用网络编码，但为了降低解码复杂度，他们采用置信传播解码器而非高斯消元解码器。为此，他们采用了LT码的编码机制，并在每个节点上以大量计算和内存为代价维持节点间的RSD。Champel 等人[2010]所考虑的场景与Puducheri 等人[2007],、 Sejdinovic 等人[2009],以及Liau 等人[2011]所考虑的场景之间的主要区别在于，前者针对的是广播场景，而后者及本文提出的算法试图解决多对一场景。Champel 等人[2010]的算法以增加额外延迟为代价降低了开销；而在Puducheri 等人[2007],、Sejdinovic 等人[2009],、Liau 等人[2011]以及本文的算法中，中继即时响应以减少整体开销。此外， Champel 等人[2010]假设节点之间存在反馈信道，而我们的场景中不存在反馈，仅存在从目的地到中继以及从中继到源的成功解码确认消息。

塔拉里和拉赫纳瓦德 [2012]研究了具有不等错误保护特性的分布式无率码。他们提出了用于两个源的Y型网络场景中不等错误保护的DU‐无率码。在其算法中，中继基于两种概率进行操作：分别来自每个源的接收的数据包在不使用网络编码的情况下进行转发的概率，以及组合数据包进行转发的概率。他们的方法是将这些概率与所使用的度分布联合优化为了为更重要的符号提供所需的符号错误保护，在源处进行编码。

3. 网络模型

在本节中，介绍了Y型网络场景下的网络模型及相关假设。在此考虑的场景中，源与目的地之间的通信通过单个中继进行，如图1所示。所有信道均被假定为删除信道，可能具有不同的删除率。在本文其余部分中，我们将源符号和编码符号分别称为源数据包和编码数据包。

各个源的源数据包数量可以不同，但要求数据包的大小相同。我们用S l = 1 l … 和K分别表示每个源及其源数据包数量，其中l,,T，T为与中继通信的源数量。我们将源数据包总数定义为K= ∑T l=1Kl。在我们的模型中，源与中继之间也无需同步通信。每个源根据标准LT码对其源数据包进行编码，并将编码数据包发送至中继。各源均不知道同时与中继通信的源的数量。在中继端，假设有有限的内存用量用于存储从不同源接收到的若干编码数据包。中继可以选择直接转发其中一个接收到的数据包，而不是对其进行异或组合。换句话说，中继同时具备网络编码和BnF两种选择。

对于目的地而言，来自不同源的数据包具有相同的优先级。假设目的地使用置信传播译码器对接收的数据包进行解码。

在所有源数据包成功解码后，目的地将向中继发送一个确认消息，以终止该会话。从目的地的角度来看，中继是一个具有K个源数据包的源节点，该节点使用LT码对这些数据包进行编码。目的地处的置信传播解码器的性能完全取决于在目的地接收到的编码数据包的度分布。因此，中继的主要目标是对从源接收到的编码数据包进行再编码，使得在目的地接收到的编码数据包的度分布遵循RSD。RSD定义如下：

定义 3.1. 鲁棒孤子分布 令 R= c · ln(K/δ)·√K对于 δ ∈（0, 1]和正数常数 c，则长度为 K的RSD定义为

$$ P_{RS}(i)= \frac{\rho(i)+ \tau(i)}{\sum_{l=1}^{K} \rho(l)+ \tau(l)}, \text{ for } i= 1,…, K, $$

其中

$$ \rho(i)=\begin{cases}1/K & \text{for } i= 1, \ 1/(i(i -1)) & \text{for } i= 2,…, K,\end{cases} $$

$$ \tau(i)= \begin{cases}R /(i \cdot K) & \text{for } i= 1,…,\lfloor K/R\rfloor -1\ R \cdot \ln(R/\delta)/K & \text{for } i= \lfloor K/R\rfloor,\ 0 & \text{for } i= \lfloor K/R\rfloor+ 1,…, K.\end{cases} $$

δ是置信传播解码器在接收到 K+O(√K · ln(K/δ) 2 ) 个编码符号的情况下，无法恢复所有源符号的概率。

公式(1)中的分布 ρ被称为理想孤子分布。

4. 自适应分布式LT（ADLT）编码算法

在本节中，我们提出了一种ADLT算法，用于在Y型网络场景下实现目的地的RSD。在目的地实现RSD的主要困难在于中继节点无法获取所有源数据包。因此，与源节点不同，它无法生成从RSD中选择的所有度。为解决此问题，ADLT算法使中继节点仅从“可能度数集合” 中选择度。该集合包含能够生成相应数据包的度。此外，为了在目的地获得期望的度分布， ADLT算法采用一种称为度分布更新（DDU）的技术。通过该技术，中继节点的度选择过程能够遵循在目的地所期望的期望度分布。在ADLT算法中，假设中继节点不对从源接收到的编码数据包执行高斯消元（GE）或置信传播解码（BP解码）。一旦目的地解码完某个源节点的全部源数据包，便会向中继发送一条确认消息。随后，中继节点将该源的编码数据包排除在生成新编码数据包的过程之外。相应地，中继节点向已解码的源发送确认消息以终止其传输。如果会话中仅剩一个源节点，中继节点仍继续执行ADLT算法，而不是简单地转发从剩余源节点接收到的编码数据包。

简而言之，ADLT算法包含两个主要子程序。第一个是度数选择和输出分组生成过程，该过程选择再编码数据包的度，并利用中继内存中保存的数据生成再编码数据包。第二个是DDU例程，用于维持RSD作为传输到目的地的再编码数据包的度分布。为了保存从源接收到的编码数据包，ADLT算法设有内存管理过程，本节将对此进行说明。由于中继节点的内存有限，因此采用了该过程。在ADLT算法中，在中继节点处，新再编码数据包的生成与从源接收的数据包的保存是独立进行的，无需任何同步。这使得ADLT算法能够适应源的传输速率不同的场景。下文将详细解释ADLT算法。

4.1. 度数选择和输出数据包生成

在本节中，详细解释了ADLT算法用于选择编码数据包（将传输到目的地）的度以及生成具有所选度的编码数据包的机制。使用ADLT算法形成每个要传输到目的地的数据包时，中继需要构造允许度和可能度的集合（SiAnP）。SiAnP是可能度数集合（Si Possible）与允许度数集合（Si Allowed）的交集。

可能度数集合（Si Possible）被定义为利用中继器内存中的数据包可以生成的度。当来自同一组源数据包的两个LT编码数据包进行异或操作时，所得数据包的度不一定等于原始数据包度的和。因此，若在可能度数集合（Si Possible）中考虑更广泛的源内组合，将增加所提算法的计算复杂度。因此，在本文中，我们将可能度数集合限制为以下集合可生成的度：{M1, M2, M1⊗M1, M2⊗M2, M1⊗M2}。其中，M1和M2分别表示从中继从源1和源2接收到的编码数据包集合。集合{Mi ⊗Mj}表示通过从源i和源j接收到的编码数据包进行异或组合所得的数据包集合。在第5节中，我们研究了进一步考虑源内组合对ADLT算法整体性能的影响。需要注意的是，将集合{M1}和{M2}包含在(S i Possible)中，使中继具有选择的余地除了通过网络编码获得的数据包外，仅转发其内存中的一个数据包（不进行网络编码）。

允许的度集合 SiAllowed 是指在更新中具有概率的那些度 d PDF (Pi) 大于零。换句话说，

$$ SA_{allowed}={j: P_i(j)> 0}. \quad (2) $$

更新后的概率分布函数（Pi）是在第i次传输后从DDU获得的概率分布函数。DDU过程在第4.2节中进行了说明。

在形成SiAnP后，中继节点必须生成一个新的PDF（Pi AnP），下一个数据包的度将根据该PDF进行选择。此PDF定义如下：

$$ P_{i \ AnP}(j)=\begin{cases}P_i(j)/\beta_i & \text{for } j \in Si \ AnP, \ 0 & \text{Otherwise.}\end{cases} \quad (3) $$

其中 βi= ∑j ∈Si AnP Pi(j)是归一化常数，Pi是由中继到目的地的前一次传输获得的更新后的度分布。Pi初始设置为RSD(PRS)。

如果 Si AnP 恰好为空集合，则上述度选择过程将失败。换句话说，Si Allowed 与 Si Possible 之间没有交集。向 Si Possible 添加新的度不可行。因此，为了避免 Si AnP 为空，应将 Si Allowed 调整为适应 Si Possible。为此，如果 Si Allowed 与 Si Possible 之间没有任何交集，则我们将 Pi 重置为 RSD（PRS），并形成新的允许度集合（Si Allowed）。

一度数据包的例外情况。一度数据包对于启动BP解码过程非常重要。因此，在ADLT 算法中，特别优先将一度数据包转发至目的地。如果一度存在于SiAnP中，则以概率一选择一度作为从中继到目的地的下一次传输的数据包的度。

组合选择子程序。在选择度之后，中继需要利用其内存中保存的编码数据包来生成再编码数据包。通常，对于所选的度存在多个可能的组合。用于选择组合的方法直接影响目的地接收到的LT码流的输入度分布。在ADLT算法中，根据称为传输次数(TN)的指标来选择合适的组合。源数据包的传输次数(TN)是指该源数据包被包含在从中继传输到目的地的编码数据包中的次数。通过在中继节点为每个K个源数据包维护一个计数器，可以计算源数据包的TN值。编码数据包的TN等于其在LT码的Tanner图中相邻源数据包的TN之和。

中继节点形成前BCS个具有最小TN的可能组合的列表，并从中均匀随机选择一个。我们将BCS称为组合选择的缓冲区大小，它是一个系统参数。我们不选择具有最小TN的组合，因为它在实际中的性能较差。在标准LT码中，源数据包是均匀采样的，因此输入度分布为泊松分布。选择具有最小TN的组合类似于对源数据包的TN进行注水，这会使输入度分布趋向于狄拉克δ函数，从而在实际中表现不佳。在生成待传输至目的地的数据包后，用于形成再编码数据包的原始编码数据包将从中继的内存中擦除。

4.2. 度分布更新

在本小节中，介绍了ADLT算法的主要机制——DDU方法。该方法负责保持RSD作为在目的地接收到的编码数据包的度分布。DDU在中继节点每次向目的地传输编码数据包后执行。该技术以降低所选度的概率、同时提高其他度的概率的方式优化度分布。DDU的最终目标是使目的地接收的数据包的度分布在平均意义上遵循RSD。

定义 4.1. 度分布更新（DDU） 设 di 为从中继传输到目的地的第 i 个传输索引处所发送数据包的度。假设 P(i−1) 和 Pi 分别为 DDU例程 前后的度分布，则 Pi 可基于 P(i−1) 定义如下：

$$ P_i(j)= \begin{cases} \frac{(N’ -(i -1))\cdot P_{i-1}(j)-1}{(N’ -i)} & \text{for } j= d_i, \ \frac{(N’ -(i -1))\cdot P_{i-1}(j)}{(N’ -i)} & \text{for } j \neq d_i. \end{cases} \quad (4) $$

j在(4)中从1变化到K，而N′是从中继到目的地成功解码的期望总传输次数的估计值。（N′ −i）仅仅是成功解码前剩余的期望传输次数。比较P(i−1)和Pi，di的概率降低，而其他度的概率增加。当P(i−1)(j)取接近零的非常小的正数值时，项（N′ −(i − 1） · Pi−1(j) − 1可能具有负值。在这种情况下，我们将Pi(di)设为零，并将分布Pi归一化为1。我们将此过程的这一部分称为零映射。

有人可能会问，N′ 的正确值是什么？并且，如果解码器在接收到 N′ 个编码数据包后仍无法恢复所有源数据包（由于删除），那么为了避免 DDU 例程中出现非正数（N′ −i），应该采取什么措施？

设置N的值′。 为了为N′选择一个合适的值，我们首先必须比较初始起始分布与使用 DDU例程采样的度分布之间的相似性。初始起始分布是DDU例程在开始选择度之前给定的度分布。这里，我们选择全变差（TV）距离作为比较两个分布相似性的度量。全变差（ TV）距离定义如下。

定义 4.2. 全变差（TV）距离 [Denuit 等，2005，第 393] 页 393] 两个概率分布 px 和 qx 之间的总变差距离由以下公式定义

$$ D(px, qx) \equiv \frac{1}{2} \cdot\sum_x |px -qx|. \quad (5) $$

总变差距离等于两个概率分布之间L1距离的一半。很容易证明[Denuit 等人 2005]，该总变差距离的定义与以下表达式相同：

$$ D(px, qx)= \max_S |p(S)−q(S)| = \max_S |\sum_{x\in S} px -\sum_{x\in S} qx| . \quad (6) $$

在方程（6）中，最大化是针对样本空间的所有子集S进行的。被最大化的量是事件S根据分布{px}发生的概率与事件S发生根据分布{qx}。因此，在尝试区分分布{px} 和 {qx} 时，事件 S 在某种意义上是用于检验的最佳事件，而总变差距离决定了能够多好地进行这种区分。对于总变差距离的数值计算， 我们采用公式(5)。

总之，我们通过优化N′的值，旨在找到N′与N（成功解码前的预期编码符号数）之间的线性关系。为此，第一步是找到使给定N值下总变差距离最小的N′值。这是通过固定N′的值执行 DDU例程，并测量DDU例程的初始分布（即RSD）与通过DDU例程选定的度所获得的度分布之间的总变差距离来实现的。

每次使用DDU例程进行度数选择后，会获得一个新的度分布作为目的地接收到的度分布。因此，在每次通过DDU例程进行度数选择后，两个分布之间的总变差距离都会发生变化。这样，对于给定的N′值，总变差距离可表示为N（成功解码前的预期编码符号数）。

作为通过DDU例程选定的度所获得的度分布的一个示例，考虑以下情况：度3是 DDU例程选择的第一个度，则第一次选择后获得的度分布为 δ(d − 3)。类似地，如果第二个选定的度是2,则第二次选择后获得的度分布为 0.5 × δ(d−2) + 0.5 × δ(d −3)。

关于N′的优化，假设中继节点可以访问所有源符号。换句话说，假设S Possible={1, 2,…,K}。这样做是为了在Y型网络场景中，使N′的优化独立于中继器内存中度的可用性所引入的随机性（反映在SPossible中）。

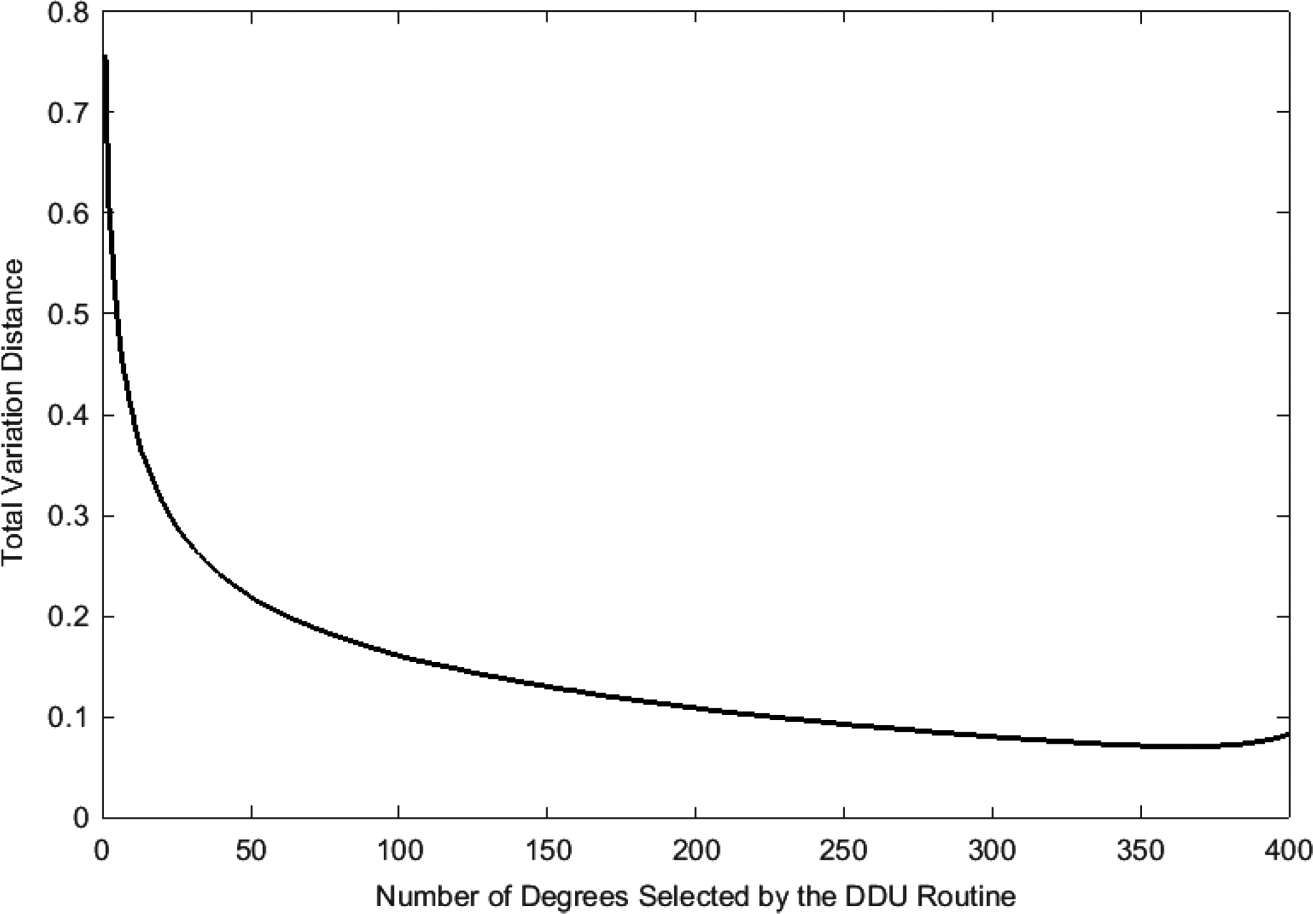
在图2中，当N′设为400且有K= 300个源符号时，展示了TV距离随样本数量的变化情况，以及参数为 δ= 0.5、c= 0.05的RSD作为初始分布。在图2所示的图中，359个样本时获得最小的总变差距离。然后我们可以提取对应于最小总变差距离的N值。

我们对不同的N′值执行此过程，以获得相应的N值，从而针对每个N′值得到最小的 TV距离。在图3中，导致最小TV距离的N值以N′值的形式表示。

下一步，我们将所得到的点拟合为一个线性多项式，以便通过关系式N′= c1 · N+ c0来近似描述N′与N（编码符号的期望数量）之间的关系。在表I和表II中，针对具有k = 300个源符号的情况，给出了不同初始起始分布（RSD参数的值）对应的系数c1和c0。注意，根据初始起始分布以及用于度量初始和采样度分布相似性的度量指标的不同，所得 系数c1和c0的值也不同。

在ADLT算法中，我们选择N′的初始值等于(N′= c1 · N0+c0)，其中N0被设置为在无损信道上对标准LT码进行解码前已传输的编码分组总数的第90百分位数。该值对于具有K= 300个源符号和以 δ= 0.5及c= 0.05为参数的RSD作为初始度分布的LT码，N0等于391。

如果已传输的编码分组数量达到N′ −N′ Threshold，那么N ′的值将根据以下公式进行更新，

$$ N’= c_1 \cdot N_0 (1 -e) + c_0, \quad (7) $$

其中e表示信道的删除率。N′ Threshold是已传输的编码分组数量（N）与N ′之间的最小允许差值。设置该差值是因为N′与已传输编码分组数量之间的差值是公式(4)的分母，当该差值趋近于较小时，会导致过多的零映射，从而降低ADLT算法的性能。在我们的仿真中，将e （在方程(7)中）的值以0.1的步长从0.1逐步增加到0.9。在我们的仿真中，N′ Threshold的值设为37,，即N′的初始值与N0之间的差值。

LEMMA 4.3. 使用DDU的平均分布

使用DDU方法选择编码数据包的度分布平均而言将与初始分布相同，如果忽略DDU方法中的零映射。

PROOF。 对于给定的Pi−1，根据di的值，更新后的分布Pi可能是K种不同的分布之一。我们定义 i−1和 i分别为Pi−1和Pi所有可能分布的集合。我们关注包含在i−1和 i中的分布的平均行为。我们定义 ¯Pi−1和 ¯Pi分别为 i−1和 i中所有分布的平均分布。利用公式(8)， ¯Pi可以表示为 ¯Pi−1的矩阵形式如下，

$$ \begin{bmatrix} \bar{P} i(1) \ … \ \bar{P}_i(K) \end{bmatrix}= A\times \begin{bmatrix} \bar{P} {i-1}(1) \ … \ \bar{P}_{i-1}(K) \end{bmatrix} \quad (8) $$

with

$$ A=\frac{(N’ -(i -1))\times[\bar{P} {i-1}(1),…, \bar{P} {i-1}(K)]^T \times \mathbf{1} - I_K}{N’ -i} $$

其中1是长度为K的全1行向量，IK是大小为K的单位矩阵。需要指出的是，公式(8)成立的前提是(N ′ −(i −1))×[ ¯ i−1(1)… ¯ i−1(K)] T × 1 − K没有任何负元素。换句话说，公式(8)在DDU例程中未考虑零映射。求解公式(8)，可以推导出 ¯Pi(j) = ¯Pi − 1(j) 对所有j ∈[1,K],且∀i ∈[1,N ′ −1]成立。

的系数c1)

4.3. 中继节点的内存管理

在本节中，描述了ADLT算法用于管理中继节点内存的过程。中继节点为从每个源接收到的数据包提供有限的内存。因此，内存溢出是不可避免的，特别是当通过该中继传输的源数量超过两个时。在此，我们提出了一种策略，用于将新接收到的数据包保存到每个源对应的中继专用内存中。此处的内存指的是中继为从特定源节点接收到的编码数据包所分配的专用内存。如果内存中有空闲空间，则接收到的数据包将以概率一被保存。

我们为每个编码数据包定义了一个新参数，称为平均传输次数（ATN），即该编码数据包的传输次数（TN）除以其度。当内存满时，将接收到的编码数据包的平均传输次数（ATN）与内存中已保存的编码数据包的平均传输次数（ATN）进行比较。如果内存中存在某个编码数据包的平均传输次数（ATN）更高，同时其度也更高或相等，则用接收到的数据包替换该编码数据包。

4.4. 传输速率

在本节中，分析了源节点和中继节点的传输速率对ADLT算法性能的影响。源和中继的传输速率在ADLT算法的性能中起着重要作用。在所有先前提出的算法[Puducheri等，2007； Sejdinovic等，2009；Liau等，2011；塔拉里和拉赫纳瓦德 2012],中，均假设源和中继的传输速率相等，而ADLT算法放宽了这一约束。在本节中，我们研究中继和源的传输速率对中继内存以及相应的允许度和可能度集合（SiAnP）的影响。我们将这些影响称为中继处的内存溢出和空内存。当中继的传输速率相对于源较低时会发生内存溢出，而当中继的传输速率高于源时则会出现空内存情况。我们关注的是发生内存溢出和空内存时中继传输速率的阈值。

这里，我们考虑具有两个源的Y型网络的情况。设RS1和RS2为两个源的符号传输速率， RR为中继的符号传输速率。e1,、e2,和eR分别为链路S1‐R、S2‐R和R‐D上的删除率。我们定义 γ1和 γ2为从中继转发到目的地的、仅来自源且在中继处未进行任何异或操作的分组所占的比例。相应地，γ1,2定义为在中继处通过对来自两个源的分组进行异或组合而获得的传输分组所占的比例。注意γ1+ γ2+ γ1,2= 1和0 ≤ γ1, γ2,γ1,2 ≤ 1。假设传输从时间零开始，在给定时间t，中继已从源一接收到t × RS1 ×(1 − e1)个数据包，并向目的地传输了t × RR个数据包，其中t×RR×(γ1+γ1,2)个被选中并从内存一中删除。如果t× RR×(γ1+γ1,2) >t× RS1×(1−e1)，则在时间t会发生空内存。利用该不等式，(RS1 ×(1 − e1))/(γ1+ γ1,2)可被视为使MR为空时R1的上限。此处，M1指中继专用于从源一接收的数据包的内存。类似地，(RS2 ×(1 − e2))/(γ2+ γ1,2)是使MR为空时R2的上限。在图4(a)中，我们绘制了差值RR− (RS1×(1−e1))/((γ1+γ1,2))随RR变化的曲线，以及ADLT算法在仿真中经历的空内存百分比。空内存百分比是指内存M1为空的时间持续与总传输时间(tT)之比（以百分比表示）。从图 4(a)可以看出，一旦RR超过前述阈值(RS1 ×(1−e1))/(γ1+γ1,2)，中继处的空内存百分比便开始从零上升。这意味着一旦中继的传输速率(RR)超过上限(RS1 ×(1 − e1))/(γ1+ γ1,2)，内存M1在传输完成前的某些时刻将开始变为空。换句话说，只要中继的传输速率(RR)小于上限(RS1 ×(1 − e1))/(γ1+ γ1,2)，内存M1就永远不会为空。

如果在时间t满足t ×RS 1 ×(1−e1) −t ×RR×(γ1+ γ1,2) > | M1|，则会发生内存溢出，其中 | M1| 为内存一的大小，即内存一中可保存的数据包最大数量。该不等式可写为如下形式：

$$ \frac{RS_1 (1 -e_1)}{RR} -(\gamma_1+ \gamma_{1,2})>\frac{|M_1 |}{K} \left( \frac{t}{t_T} \right)(1+ \varepsilon) , \quad (9) $$

其中，K是两个源的源数据包总数，tT是总传输时间。 ε是开销。在以下不等式中，我们使用了这一事实：tT×RR是从中继传输到目的地的编码数据包总数，也等于K×(1+ε)。之前给出的不等式所得到的阈值并不确定，因为参数t是一个变量。作为替代方法，对于给定的RR，我们求得使前述不等式两边相等的阈值(t/tT)。我们将该阈值(t/tT)称为相对溢出时间。如果所得的(t/tT)值为正数且小于一，则会发生内存溢出；否则不会发生。

在图4(b)中，我们绘制了相对溢出时间以及通过仿真得到的内存溢出百分比随中继传输速率（RR）的变化关系。内存溢出百分比是指内存溢出发生的时间持续时间与总传输时间（tT）之比的百分比。在图4(b)中，相对溢出时间（t/tT）的负值是由于当式(9)右边的项在RR大于某一数值时变为负数所致。从图4(b)可以明显看出，当中继传输速率RR的值等于或大于1.6时，内存溢出百分比达到零，即不再发生内存溢出，在整个传输时间内，从源节点一接收到的所有编码数据包都可以保存在其专用内存中。

空内存的阈值（RR −(RS1 ×(1−e1))/((γ1+ γ1,2))）以及空内存百分比随RR的变化情况。(b) 相对溢出时间（t/tT）以及内存溢出百分比随RR的变化情况。此处考虑的Y型网络具有2个源，分别有K1= 600、K2= 400个源数据包和传输速率RS1= 1.2、RS2= 1。假设信道为无损信道，且此处使用的ADLT算法参数为 | M1| = 60、 | M2| = 40和BCS= 100。)

中继（即，M1）。对于相同的RR值（即，大于或等于1.6），相对溢出时间（t/tT）大于1，这意味着不会发生内存溢出。从图4可以明显看出，所得到的空内存和内存溢出的阈值几乎是准确的。微小的波动是由于在计算空内存阈值和相对溢出时间时，我们使用了通过仿真获得的γ1和γ1,2的期望值。注意，γ1、 γ2和γ1,2 vary随RR的变化而变化。需要指出的是，在本文所呈现的其余仿真结果中，我们假设源和中继的传输速率相等。这样做是为了能够与先前为该场景提出的算法[Puducheri等，2007；Sejdinovic等， 2009；Liau等 2011]进行公平比较。

5. 仿真结果

在本节中，给出了ADLT算法以及其他在文献[Puducheri等，2007；Sejdinovic等， 2009；Liau等 2011]中先前提出的算法的仿真结果。本次仿真的主要目的是在信道非无损的更实际场景下，比较ADLT算法与其他算法的性能。所模拟的算法中包括父LT码（PLT），即具有K个源数据包的单源单宿标准LT码。将PLT纳入仿真的主要原因是了解理想性能，即中继能够像拥有K个源符号的源节点一样完美生成编码数据包。我们比较中的主要参数是在目的节点观察到的解码开销（使用置信传播解码器）。开销定义为(n−K)/K，其中n是在目的节点接收到的编码数据包数量。

中继节点中ADLT算法所使用的内存用量被表示为允许保存的（来自特定源的）最大编码数据包数量与（来自同一源的）源数据包数量之比（以百分比表示）。例如，当提到ADLT算法使用60%内存时，意味着最多只能保存来自源l（具有Kl个源数据包）的 0.6 × Kl个接收到的编码数据包。因此，中继节点用于保存接收数据包的最大内存总量为 0.6 × K。我们采用相同的方法来描述SLRC算法[Liau等 2011]在中继节点中使用的内存用量。此外，在SLRC算法[Liau等 2011],中，参数 λ的值被设定为0.95，这是Liau等[2011]中计算出的最优值。在SDLT算法[Sejdinovic等 2009],中，中继节点应用了二级编码分布()，其最优值来自Sejdinovic等[2009]中提出的线性规划。我们在仿真中使用的()的数值为 1= 0.933, 2= 0.067。本节所示结果中，RSD的参数为c= 0.05, δ= 0.5。所有仿真均在C++和MATLAB环境中进行。在ADLT算法中，中继节点需要知道每个源节点中的源符号数量，但源节点无需知道其他节点的源符号数量。这一点不适用于本节仿真的其他算法，因为在这些算法中，源节点必须知道与其通信的每一个其他源节点的源符号数量。

2个源，每个含150个源数据包；(b) 3个源，每个含100个源数据包；(c) 4个源，每个含75个源数据包。)

在图5中，我们将ADLT算法与DLT [Puducheri等人2007],、SDLT [Sejdinovic等人 2009],以及SLRC [Liau等人 2011]算法在具有两个、三个和四个源的Y型网络的理想无损信道中进行了比较。此外，图5还展示了另外两种方法BnF和PLT码的结果。每个图表均以箱线图的形式显示开销分布。箱体从第一四分位数延伸到第三四分位数；中位数用红线标记。须延伸从箱子的边缘延伸到数据集的最小值和最大值，但不超过四分位距的1.5倍。此外，离群值用红色加号单独标出。PLT码是具有K个源数据包的单源单宿标准LT码。在BnF方法中，中继节点依次转发从源接收到的数据包，不作任何更改。例如，在两个源的情况下，来自源一（源二）的数据包在传输的奇数（偶数）索引中被转发至目的节点。使用BnF方法时，在目的节点接收到的输出度分布是两个RSD的和，每个分别具有K1和K2个元素。值得注意的是，在目的地期望的最优度分布是一个具有K1+ K2个元素的RSD。ADLT算法以及 Puducheri等人[2007],、Sejdinovic等人[2009],和Liau等人[2011]提出的算法旨在为目的节点提供这样的度分布，以保持LT流的最优性能。

正如预期，PLT码表现最佳，紧随其后的是DLT[Puducheri等人 2007]提出的算法。这是因为在具有两个的Y型网络中，DLT算法[Puducheri等 2007]在信道无损时可实现精确的RSD。SLRC算法[Liau等 2011]在图5(a)中的四分位距最短，相较于其他算法。这是由于在目的节点接收到的度分布中，二度数据包占比较高所致。ADLT算法在图5(a)中性能较差，原因在于其无法在目的节点完美重构预期的RSD。这是由于中继节点接收到的编码数据包平均度较高，降低了在中继节点再生低度编码数据包的可能性。需要注意的是，在RSD中，大部分概率集中在低度。对于具有三个和四个源的Y型网络，这种影响减弱，ADLT算法的性能在图5(b)和图5(c)中更接近PLT。

为了在真实场景中将ADLT算法与其他算法进行比较，我们在图6(a)中模拟了ADLT算法以及DLT [Puducheri等人 2007],、SDLT [Sejdinovic等人 2009],、SLRC [Liau等人 2011],和BnF算法。

包含2个源，每个源有150个源数据包，(b)包含3个源，每个源有100个源数据包，(c)包含4个源，每个源有75个源数据包。)

以及在存在删除的情况下，Y型网络中两个源的PLT。在图6(b)和图6(c)中，分别在具有三个和四个源的Y型网络中进行了类似的仿真。对于图6中呈现的结果，我们考虑了Y型网络所有信道上的删除情况，即从源到中继的信道以及从中继到目的地的信道。在图6中，我们用于比较的主要指标是目的地成功解码所需的不同算法的平均开销。根据图6所示的结果，在高删除率情况下，ADLT算法优于其他算法，并且相比其他算法能够更接近PLT。当源数量超过两个时，这一优势更为明显。从图6的结果可以看出，与中继到目的地信道上的删除相比，源到中继信道上的删除对 ADLT算法性能的影响较小，而前者的影响是不可避免的。

中继处ADLT算法所需的内存量是一个重要参数。为了研究ADLT算法对中继可用内存数量的依赖性，图7展示了在不同中继可用内存条件下，ADLT算法的成功解码概率随开销的变化情况。成功解码概率是指目的节点中的置信传播解码器能够从所有源节点完全解码出所有源数据包的概率。图7所示结果是在无损信道条件下获得的。显然，随着中继可用内存的增加，ADLT算法的性能得到提升。这是符合预期的，因为更大的内存允许中继节点保存更多的编码数据包，从而产生更大的可能度数集合（SPossible）。这导致了更大范围的可能和允许的度数集合(SAnP)，该方法通过保持LT码在目的地接收到的输出度分布为RSD，从而提升了DDU技术的性能。

ADLT算法的一个重要参数是组合选择子程序中使用的缓冲区大小（BCS）。在图8中，我们绘制了在具有两个源的Y型网络中，不同BCS值下ADLT算法的平均开销。图8所示结果假设所有信道均为无损信道，并且内存设置为40%。

从图8可以看出，当BCS取值较小时，ADLT算法的性能会下降。这是因为当BCS取值较小时，在目的地观察到的源符号度分布趋向于狄拉克δ函数而非泊松分布。在标准LT码中，源符号的度分布遵循泊松分布。因此，BCS应大于某个特定值，以使源符号的度分布呈现预期的泊松分布。从图8可以得出，BCS的这一阈值约为100。随着源数量的增加， ADLT算法达到最佳性能所需的BCS阈值也随之增加。这是由于给定目标度的可能组合来自各源接收到的编码数据包集合的笛卡尔积。因此，源数量越多，可能的组合数量也越多， ADLT算法要实现最佳性能就需要更大的BCS。

Si Possible中包含的组合集合。在第4节中，我们提到为了形成可能度数集合（Si Possible），我们将ADLT算法限制在以下组合：{M1,M2,M1⊗M1,M2⊗M2,M1⊗M2}。在此，我们分析引入更广泛的源内组合对ADLT算法整体性能的影响。为此，我们定义了三种组合阶数。设M1和M2分别为从中继器内存中保存的、从第一和第二源接收到的编码数据包集合。组合阶数一包含以下组合集合：{M1, M2,M1 ⊗ M1, M2 ⊗ M2, M1 ⊗ M2}。在组合阶数一的基础上，组合阶数二增加了以下组合：{M1 ⊗ M1 ⊗ M1,M1 ⊗ M1 ⊗ M2,M1 ⊗ M 2 ⊗ M2,M2 ⊗ M2 ⊗ M2}。类似地，在组合阶数二的基础上，组合阶数三进一步增加了以下组合：{M1 ⊗ M1 ⊗ M1 ⊗ M1,M1 ⊗ M1 ⊗M1 ⊗ M2, M1 ⊗ M1 ⊗ M2 ⊗ M2,M1 ⊗ M2 ⊗ M2 ⊗ M2, M2 ⊗ M2 ⊗ M2 ⊗ M2}。图9展示了ADLT算法在所有三种组合阶数下成功解码概率随开销的变化情况。从图9的结果可以看出，增加组合阶数并在可能度数集合中引入更多组合，能显著降低ADLT算法的整体开销。但这种改进是以增加中继节点的计算负载为代价的。

6. 结论

本文中，我们提出了用于Y型网络拓扑中分布式LT编码的ADLT算法，其中多个源通过同一个中继与一个目的地通信。Y型网络拓扑被视为一种抽象收集树方案在传感器网络中用于收集信息。ADLT算法在中继节点执行网络编码技术以减少开销，并采用DDU技术在目的地维持RSD。ADLT算法的所有复杂性均位于中继节点，源无需知晓网络拓扑或与同一中继同时通信的源数量。与先前提出的算法相比，ADLT算法的主要优势在于其灵活性，能够管理不同数量的源、不同数量的源符号以及不同的传输速率。通过仿真验证，即使在存在删除的情况下，ADLT算法在开销方面也能实现接近标准LT码的性能。相较于其他先前提出的算法，ADLT算法还具有适应不同数量的源、不同数量的源数据包以及不同传输速率的优势。