​MySQL索引的底层数据结构及算法

我们经常在涉及到SQL优化的时候，总是会想到加索引。那索引究竟是个什么玩意儿？

索引是帮助MySQL高效获取数据，并且排好序的数据结构。

我们知道MySQL可以采用的是B+树和hash来维护索引的，hash这个结构并不常用，它虽然能够通过hash算法很快的路由到对应的数据，但是对于排序，hash就显得很鸡肋了。

树形结构在一定程度上，都是采用的二分查找，所以查询的时间复杂度都很低。

但随之而来又面临一系列的问题，比如树的退化，以及随着数据的不断增加，树的高度越来越高，磁盘IO的次数越来越多，导致性能越来越低，查询的时间越来越不可控。

打个比方:

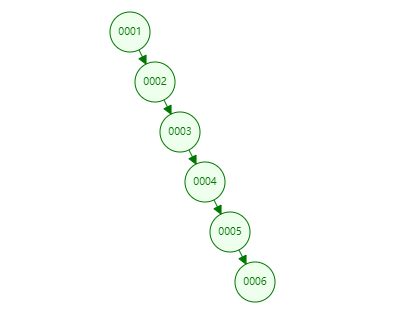
二叉树

在极端的情况下，二叉树会退化成链表，查询的时间复杂度也随之退化。且树的高度越来越高。

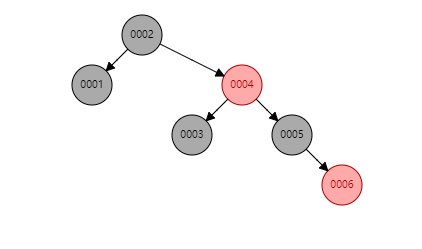
红黑树

它又叫二叉平衡树，虽然自旋和变色解决了退化成链表的问题，但在一定程度上，树的高度递增的问题还是没有得到解决。

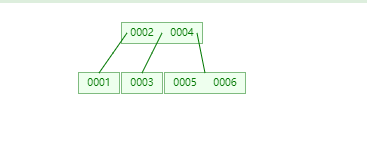
B树

它相当于是二叉树的一个进化版本，变成了多叉树，那么单个结点存储的数据就变多了，随之树的高度也得到了控制。

但是B树有一个特点，它的每个结点都存储了对应行的data。那么我们可以试想一下，这个索引的内存大小会特别大，而MySQL的内存是有限的，我们单表在大多数情况下，都不止一两个索引，那如果每个索引树都去维护一份data，这对于MySQL将会是一笔巨大的开销, 且造成了资源浪费。

另一方面，如果我们要对索引字段排序，B树会采取一系列的递归遍历，性能大打折扣。

B+树

它相当于是B树的一个进化版本, 从之前的每个结点都存储data，变为只有叶子结点存储data，且这个树的所有数据其实都在叶子结点上。

并且B+树在叶子结点维护了一个单向指针（MySQL做了优化，变为了双向指针），这个指针在很大程度上解决了我们对索引字段排序的问题。

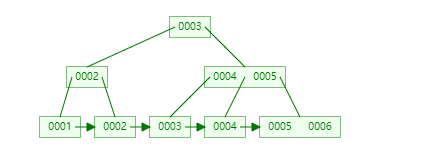
到这里，想必应该更加理解了“索引就是一个排好序的数据结构”。

PS：MySQL索引树的单个结点默认可以存储16K大小的数据，即这16K就是一个磁盘块。

意味着一个磁盘块能存储大量的索引字段，从而树的高度就得到了控制，而操作系统又有一个预读取的功能，所以每次读取索引树的时候其实就是读取一个磁盘块，把某个磁盘块的数据加载到内存中进行操作。

好了，索引的数据结构我们搞明白了，那接下来我们看一下MySQL是怎么通过这个索引树去进行快速查询的。

这里涉及到MySQL的存储引擎，像Innodb、MyISAM、 Memorry，我们就聊聊常见的Innodb和MyISAM。

PS：索引的数据结构维护在MySQL安装目录下的/data文件夹里面。

MyISAM

索引树和数据文件是分离的(非聚集)，索引树中的data维护的只是对应数据文件的内存地址，通过内存地址找到对应的数据。

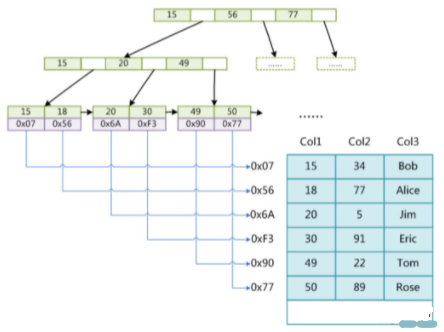
Innodb

它分为两种情况，一种是主键索引树（或者是唯一索引树），另一种是普通索引树(非聚集)。

主键索引树中的data维护的是对应行的数据，而普通索引树中维护的是对应行的主键id，通过这个主键id，去主键索引树中进行回表查询，从而找到对应的数据。

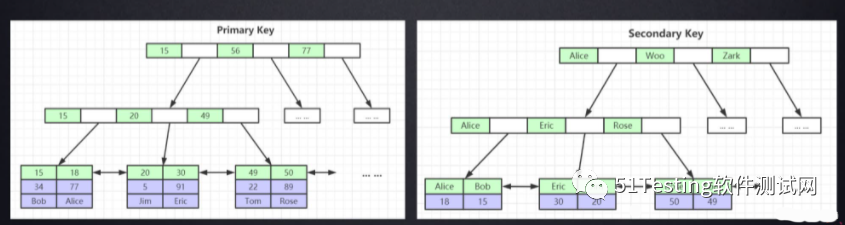
PS：大家猜想一下，MySQL的联合索引是怎么去比较大小从而构成树的呢？

打个比方，比如(name、age)这两个字段构成一个联合索引，那么会先根据name的ASCII码比较大小，如果通过name就已经确定出大小了，则不用继续去比较age的大小了。

只有当name的ASCII码相等的时候，才用去比较age的大小。

最后：下方这份完整的软件测试视频教程已经整理上传完成，需要的朋友们可以自行领取【保证100%免费】

软件测试面试文档

我们学习必然是为了找到高薪的工作，下面这些面试题是来自阿里、腾讯、字节等一线互联网大厂最新的面试资料，并且有字节大佬给出了权威的解答，刷完这一套面试资料相信大家都能找到满意的工作。