车联网中MEC卸载与资源优化

车联网中移动边缘计算的卸载与资源分配联合优化

摘要

作为物联网（IoT）技术的典型应用，车联网（IoV）正面临着爆炸式的计算需求和严格的延迟约束。基于移动边缘计算（MEC）的车联网是解决该问题的一种有前景的方法。本文聚焦于降低车联网中虚拟现实（VR）应用完成时间的问题。为此，我们提出了一种用于VR并行计算与传输的协同方法。在所提出的方案中，首先将一个VR任务划分为两个子任务。然后通过无线传输将其中一个子任务卸载到车辆上，使得这两个子任务可以分别在MEC服务器和车辆上同时处理。我们将该方案建模为一个非线性优化问题，以联合确定计算卸载比例、通信资源和计算资源分配。由于该问题具有NP难特性，设计了一种联合卸载比例与资源分配优化（JOPRAO）算法以获得最优解。仿真结果表明，通过合理地进行任务卸载和资源分配策略，VR任务的完成时间时延可显著降低。

关键词

车联网, 移动边缘计算, 资源分配, 卸载比例

引言

在过去十年中，物联网（IoT）受到了学术界和工业界的广泛关注。物联网包含生活中无处不在的设备，例如智能手机、平板电脑、电视和车辆。作为物联网的一个重要分支，车联网（IoV）已成为工业应用发展的一个新兴研究领域[1]。

然而，随着日益增长的先进车载应用的出现，车联网（IoV）中满足通信与计算需求的挑战愈发突出[2]。虚拟现实（VR）技术、自动驾驶等新应用均需处理复杂数据，对数据通信和计算能力提出了较高要求。作为车载应用，车载虚拟现实正经历前所未有的发展。由于虚拟现实应用具有计算敏感和延迟敏感的特性，当前的无线系统（如4G）无法满足无线虚拟现实应用的时延和吞吐量需求（例如VR游戏/视频）[3]。由于车载娱乐对延迟和计算能力有极高的要求，这推动了新型车联网架构[4]的发展。

移动边缘计算车联网（VEC）被广泛认为是一种满足应用需求的新范式[5]‐[6]。VEC技术将计算能力从云计算中心迁移至移动网络边缘，即无线接入网络中并靠近车辆的位置。通过在网络边缘部署计算资源，VEC允许车辆通过将任务卸载到MEC服务器来执行计算卸载。MEC服务器代替车辆执行任务，从而降低时延并提升服务质量。由于虚拟现实应用在计算后数据量会增大，将导致更多的通信数据和更长的时延。显然，决定VR任务中有多少比例在MEC服务器上执行对于降低时延至关重要。

在大多数现有的移动边缘计算研究中，许多工作聚焦于移动边缘计算网络中的计算卸载与资源分配策略[7]‐[11]。[7]‐[8]的作者研究了计算卸载策略。[7]研究了多信道无线环境下多用户移动边缘计算卸载问题，并设计了一种分布式博弈论卸载方案。在[8],中，提出了一种多轮密封顺序组合拍卖机制，以匹配移动边缘计算服务器与移动终端，从而将任务卸载到最优移动边缘计算服务器。资源分配也在[9]‐[10]中被研究。[9]通过连续凸逼近方法，在满足时延约束的条件下分配通信与计算资源，以最小化总能耗。[10]的作者研究了如何分配通信和计算资源以实现低延迟。还有一些关于卸载策略和资源分配的研究工作。[11]中的研究联合优化了卸载选择、无线资源分配和计算资源分配，以在特定应用下最小化能耗。然而，这些工作要么未研究卸载比例，要么未深入探讨计算卸载策略与资源分配的联合优化。

本文中，我们联合优化卸载比例，通信资源分配和计算资源分配，以最小化移动边缘计算车联网中的时延。综上所述，本文的主要贡献包括：
1) 我们提出了一种针对虚拟现实应用的卸载方案，以降低车联网中的时延，其中VR任务按一定比例被划分为两个子任务，并由配备MEC服务器的微基站同时计算和传输这两个子任务。
2) 我们建立了一个联合优化模型，以寻找最小的VR任务完成时间，该模型中对卸载比例（即决定将多少任务卸载到本地车辆）、通信资源分配和计算资源分配进行联合优化。
3) 为了解决这一NP难问题，提出了一种联合卸载比例与资源分配优化（JOPRAO）算法。仿真结果表明，通过合理地卸载任务以及制定资源分配策略，可以显著降低VR任务的完成时间时延。

本文其余部分组织如下。在第二节中，详细说明了系统模型。第三节中建立了优化问题模型。在第四节中，我们提出了一种联合卸载比例与资源分配优化算法来求解该最优问题。第五节给出了数值分析和仿真结果，以验证第四节所提算法的性能。第六节得出了结论。

II. 系统模型

在本节中，将描述包括网络模型、通信模型和计算模型在内的系统模型。

A. 网络模型

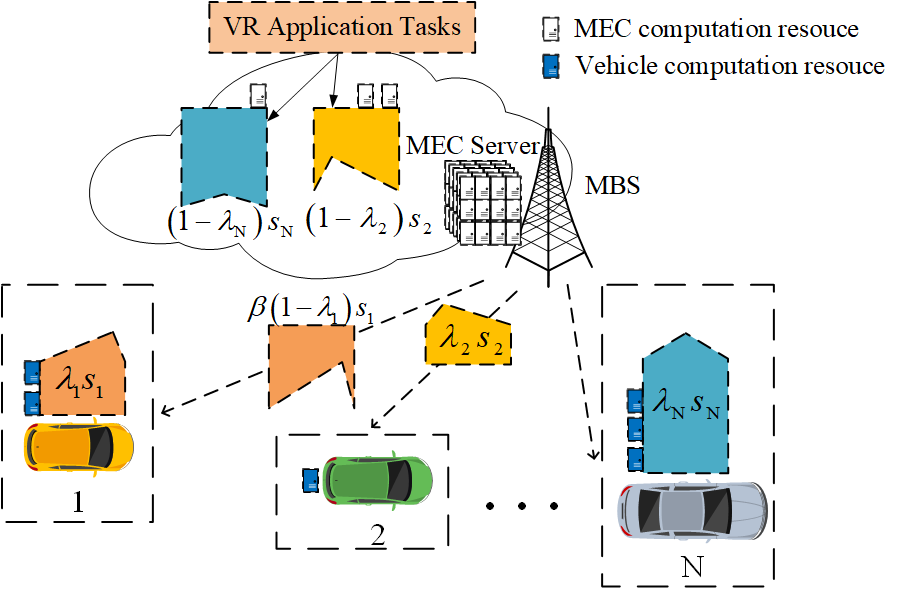
如图1所示，我们考虑一个由配备MEC服务器的微基站（MBS）和多辆车辆组成的车联网。MEC服务器提供由运营商部署在车联网边缘的VR应用服务。MEC服务器与微基站相连，并为微基站覆盖范围内的车辆提供计算资源（例如每秒CPU周期）。车辆配备有计算资源以执行VR任务。车辆集合表示为 N={1, 2, · · ·, N}，车辆总数为N = |N|。sn是车辆n的VR任务，定义为需要处理的数据量。在前述现有研究中，一个任务只能在本地车辆或远程移动边缘计算服务器上处理。在这两种情况下，完成任务可能需要较长的延迟，这是由于车辆的计算能力有限，或由于通过空中接口传输大量数据所致。为解决这些问题，我们提出任何VR任务均可被划分为两个子任务，从而使车辆能够与MEC服务器共同参与VR计算任务。为简化问题，我们假设任意任务可以按任意比例划分为两个子任务，且两个子任务之间无重叠。每个子任务可在MEC服务器或本地车辆上处理。定义卸载到车辆 n的子任务为 λnsn，其中 n ∈ N和 λn ∈[0, 1]。 λn是任务 sn的卸载比例。卸载比例向量定义为 λ=[λ1, λ2,…, λn,…, λN]T, n ∈N。这意味着车辆 n将处理子任务 λnsn，而MEC服务器将处理另一个子任务(1 − λn)sn。

本文中使用的主要符号在表I中进行了总结。

符号	定义
n	车辆索引。
k	子信道索引。
φ	计算每比特所需的CPU周期，即任务计算复杂度。
β	任务输出与输入比。
K	子信道数量。
N	车辆数量。
σ²	加性高斯白噪声的功率。
Ink	来自相邻宏基站和车辆的干扰。
λ	卸载比例向量，大小为 N×1。
λn	车辆 n的卸载比例。
C	子信道关联矩阵 , sizeof N×K.
F	MEC计算资源分配向量，大小为N×1。
W₀	一个子信道的带宽
fn,c	MEC服务器分配给车辆 n的CPU周期。
cₙₖ	指示车辆 n是否使用的二进制变量 子信道 k。
f	MEC服务器的总计算资源。
fn,l	车辆 n的本地计算能力。
pₙₖ	微基站在子信道 k上用于车辆 n的传输功率。
hₙₖ	微基站到车辆 n在子信道中的信道增益 k.
rₙ	车辆 n的数据传输速率。
rₙₖ	车辆 n在子信道 k中的数据传输速率。
sₙ	车辆 n请求的VR任务的大小。
SINRₙₖ	车辆 n在子信道 k中的干扰强度。
∆exeₙ,꜀	在MEC处理的子任务的处理延迟服务器.
∆transₙ,꜀	移动边缘计算中处理子任务的传输延迟服务器
∆exeₙ,ʟ	子任务在本地车辆上处理的处理延迟 cle.
∆transₙ,ʟ	本地处理子任务的传输延迟 车辆
Dₙ	任务 sₙ 的总体完成时间

B. 通信模型

在所关注的场景中，有 K 个可用的正交OFDM子信道可供分配给车辆进行无线传输。令 K={1, 2,…,K} 表示子信道的集合。每个子信道的带宽为 W₀。我们引入一个子信道关联矩阵C=(cₙₖ)N×K。该二进制变量表示是否将子信道 k分配给车辆 n。如果 cₙₖ= 1，表示子信道 k已分配给车辆 n，否则为 cₙₖ= 0。矩阵C中的变量受限于

$$
∑_{n∈N} cₙₖ ≤ 1, ∀k ∈ K. \tag{1}
$$

本文研究了单小区场景。因此，车辆 n使用子信道k时的干扰强度 SINRₙₖ可以按如下方式计算

$$
SINRₙₖ=\frac{pₙₖhₙₖ}{σ²ₙₖ+ Iₙₖ}, \tag{2}
$$

其中， σ²ₙₖ定义为子信道 k(k ∈ K)上加性高斯白噪声的功率， pₙₖ表示微基站在子信道 k上对车辆 n的传输功率， hₙₖ表示宏基站在子信道 k上到车辆n的信道增益。来自其他宏基站及相邻宏基站内车辆的干扰由 Iₙₖ表示。为了简化起见，我们将 Iₙₖ、 pₙₖ和 hₙₖ视为常数。

根据香农容量理论，车辆 n 在子信道 k 上实现的数据传输速率为 rₙₖ= W₀log(1+cₙₖSINRₙₖ)。因此，车辆 n 的数据传输速率可表示为

$$
rₙ(C)=∑_{k∈K} rₙₖ. \tag{3}
$$

C. 计算模型

在本小节中，我们介绍计算卸载模型。本文考虑车辆 n向MEC服务器请求一个虚拟现实视频任务 sₙ。当车辆从微基站请求虚拟现实视频任务时，MEC服务器将决定卸载比例 λ=[λ₁, λ₂,…, λₙ,…, λ_N]^T (n ∈ N)。根据 λₙ，在MEC服务器和车辆 n上处理的两个子任务的数据量分别为(1 − λₙ)sₙ和 λₙsₙ。因此，具有(1−λₙ)sₙ数据量的子任务将首先在MEC服务器上进行处理。当子任务处理完成后，微基站将把处理后的数据传输给相关车辆。与此同时，另一个具有λₙsₙ数据量的子任务通过无线信道卸载至车辆。车辆在接收到子任务后，开始利用自身的计算资源进行计算。在MEC服务器和本地车辆的计算与传输均完成后，车辆将两个结果重新组合。

接下来，我们将讨论虚拟现实视频任务的完成时间。根据之前的介绍，车辆 n 的每个任务 sₙ 都将被划分为两个子任务。显然，整个任务的完成时间取决于这两个子任务。

我们假设MEC服务器的CPU频率为 f。相应地，车辆 n 的本地CPU频率为fₙ,ʟ。一条规则是，MEC服务器的计算能力远优于任何车辆，即f≫fₙ,ʟ，对于 n ∈N。分配给车辆 n的子任务的计算资源为fₙ,꜀（CPU频率），受限于

$$
∑_{n∈N} fₙ,꜀ ≤ f. \tag{4}
$$

根据上述描述，我们定义 φ为计算每比特所需的 CPU周期，其取决于任务[12]‐[13]的计算复杂度。此外，我们将任务输出与输入比定义为 β(β ≥ 1) [14]。然后，我们可以得到在MEC服务器端处理的子任务的处理时延

$$
∆exeₙ,꜀= \frac{φ(1−λₙ) sₙ}{fₙ,꜀},
$$

和通信时延

$$
∆transₙ,꜀= \frac{β(1−λₙ)sₙ}{rₙ}，
$$

以及在本地车辆端处理的子任务的处理时延

$$
∆exeₙ,ʟ= \frac{φλₙsₙ}{fₙ,ʟ},
$$

和通信时延

$$
∆transₙ,ʟ= \frac{λₙsₙ}{rₙ}。
$$

如图2所示，只有当微基站到车辆的卸载数据传输完成后，MEC服务器才能发送处理后的数据。因此，任务 sₙ的总体完成时间可以表示为

$$
Dₙ= \max{Tₙ,꜀, Tₙ,ʟ, Tₙ,trans}, \tag{5}
$$

$$
Tₙ,꜀= ∆exeₙ,꜀+ ∆transₙ,꜀+∆waitₙ,꜀, \tag{6}
$$

$$
Tₙ,ʟ= ∆exeₙ,ʟ+ ∆transₙ,ʟ , \tag{7}
$$

$$
Tₙ,trans= ∆transₙ,꜀+∆transₙ,ʟ , \tag{8}
$$

其中，Tₙ,꜀表示在MEC服务器上处理的子任务的完成时延，Tₙ,ʟ表示在车辆上处理的子任务的完成时延，Tₙ,trans表示两个子任务的传输延迟之和。∆waitₙ,꜀表示等待信道空闲的时延。图2展示了任务完成时间的一种情况。

III. 问题建模

在本节中，将详细描述最优问题建模。对于虚拟现实视频应用，必须认真考虑时延问题。然而，根据式(5)，实现最小化时延具有挑战性。MEC服务器需要对卸载比例、通信资源和计算资源分配进行联合优化。

目标是为所有车辆提供最优的计算卸载比例策略 λ*、通信资源分配C*以及计算资源分配F*，以最小化最大任务完成时间。因此，该优化问题可表述为：

$$
\min_{λ,C,F} \max Dₙ \quad (P)
$$

s.t.
C1: (1)
C2: (4)
C3: fₙ,꜀ ≥ 0, ∀n ∈N
C4: cₙₖ ∈{0, 1}, ∀n ∈N, ∀k ∈ K
C5: $∑_{k ∈ K} cₙₖ ≥ 1, ∀n ∈N$
C6: 0 ≤ λₙ ≤ 1, ∀n ∈N

其中，F={fₙ,꜀|fₙ,꜀ ≥ 0,$∑_n$ fₙ,꜀ ≤ f, ∀n ∈N}。约束 C1确保微基站中的一个子信道最多只能被一辆车辆使用。C2是移动边缘计算服务器最大处理能力的约束。计算资源的非负性由约束 C3表示。约束C5表示每辆车辆至少被分配一个子信道。约束 C6表示卸载比例的范围。

由于以下观察结果，问题P非常难以解决且不切实际：
1) C为二进制变量这一事实使得问题P成为一个混合整数规划问题。
2) 问题P的目标函数不是凸函数。
3) 由于问题P具有NP难特性。

为了解决NP难问题P，提出了一种联合卸载比例与资源分配优化（JOPRAO）算法，用于确定计算卸载比例 λ、通信资源分配C和计算资源分配F，具体细节将在下一节中详细介绍。

四、任务卸载优化

在本节中，提出了一种JOPRAO算法，以求得非凸问题P的次优解。该算法主要包含三个步骤：子信道选择、卸载比例决策和计算资源分配。

A. 子信道选择

由于数据传输速率随车辆所使用子信道的质量而变化，因此并非所有子信道都最适合该车辆。质量较好的子信道往往会被优先选择。因此，为了为车辆选择子信道，我们综合考虑子信道质量和本地计算能力，定义车辆 n所使用的子信道 k的权重为

$$
wₙₖ= \frac{sₙ}{rₙₖ} + \frac{sₙφ}{fₙ,ʟ}, \tag{9}
$$

这意味着将整个任务卸载到车辆 n 的子信道 k时的总延迟。因此，应首先为车辆 n 选择权重最低的子信道 k。因此，车辆 n 的子信道选择规则可以描述为，

$$
k= \arg \min_{k∈K,cₙₖ=0}{ wₙₖ}. \tag{10}
$$

然后，为了最小化所有车辆中任务的最大完成时延，我们需要找到完成时延最大的车辆 n

$$
n= \arg \min_{n∈N} {Dₙ}. \tag{11}
$$

因此，我们根据(10)将子信道 k分配给车辆 n。

B. 卸载比例决策

如前所述，任务将被划分为两个子任务。为了实现问题P的目标，我们需要最小化所有车辆的最大任务完成时间。从图2可以看出，MEC服务器必须延迟其处理的子任务的数据结果传输，直到卸载数据传输完成。直观上，最小化一组变量的最大值即是使这些变量相等。因此，对于车辆 n，我们有

$$
∆exeₙ,꜀ = ∆transₙ,ʟ , \tag{12}
$$
$$
∆exeₙ,ʟ = ∆transₙ,꜀ . \tag{13}
$$

此外，根据式(12)和(13)，最优卸载比例 λₙ 以及最优计算分配fₙ,꜀和传输速率 rₙ可以表示为

$$
λₙ= 1 − \frac{φrₙ}{βfₙ,ʟ+ φrₙ}, \tag{14}
$$

$$
r²ₙ= \frac{β}{φ²} fₙ,꜀fₙ,ʟ. \tag{15}
$$

C. 计算资源分配

由于MEC服务器的计算资源有限，并非所有车辆都能被分配到最优计算资源。因此，各车辆之间存在权衡。为简化处理，MEC服务器首先将计算资源平均分配给每辆车辆，即f′ₙ,꜀= f/N。然后MEC服务器将其与最优计算资源分配f∗ₙ,꜀= (r²ₙφ)/(βfₙ,ʟ)，进行比较。如果f∗ₙ,꜀ ≤ f′ₙ,꜀，则分配给车辆 n的CPU周期将为f∗ₙ,꜀，且车辆 n将把额外CPU周期(f′ₙ,꜀ − f∗ₙ,꜀)返还给MEC服务器。如果f′ₙ,꜀ < f∗ₙ,꜀，则分配给车辆 n的CPU周期将从f′ₙ,꜀开始增加，直到超过f∗ₙ,꜀或MEC服务器无剩余计算资源可供分配。

五、数值结果

A. 参数设置

我们考虑一个配备移动边缘计算系统的车联网，该系统由一个带有MEC服务器的微基站和多个车辆组成。每辆车都有不同的虚拟现实视频任务请求。微基站在K = 50个可用子信道上进行通信。车辆数量为N= 30。网络的总信道带宽为20 MHz。因此，子信道带宽为W₀= 20/K MHz。传输功率 pₙₖ设置为20 dbm。传输链路的配置基于3GPP标准化[15]。

对于车辆，本地计算能力服从高斯分布 CN(µ₁, σ₁²)，其中均值 µ₁=700 MHz，标准差 σ₁= 50。虚拟现实视频任务的数据大小服从高斯分布CN(µ₂, σ₂²)，其中 µ₂= 80 MB且 σ₂= 10。

对于无线信道，加性白高斯噪声的功率为 σ²= −100 dbm。信道功率增益服从高斯分布 CN(µ₃, σ₃²)，其中 µ₃= 10,σ₃= 1。来自相邻宏基站 Iₙₖ的干扰服从高斯分布 CN(µ₄, σ₄²) ，其中 µ₄= 7dbm， σ₄= 1。

对于MEC服务器，我们将最大计算能力 f设置为 30 GHz。对于VR视频任务计算，计算复杂度为 φ= 2周期/比特，任务输出与输入比为 β= 30。

B. JOPRAO算法评估

在本小节中，将讨论所提出的JOPRAO算法的性能。为了评估JOPRAO算法的性能，进行了仿真。如图3所示，与在本地车辆或MEC服务器上完全计算任务相比，通过我们的算法获得的最优卸载实现了更低的任务完成时间。这意味着通过卸载比例、通信资源和计算资源分配的联合优化，可以获得更低的延迟。

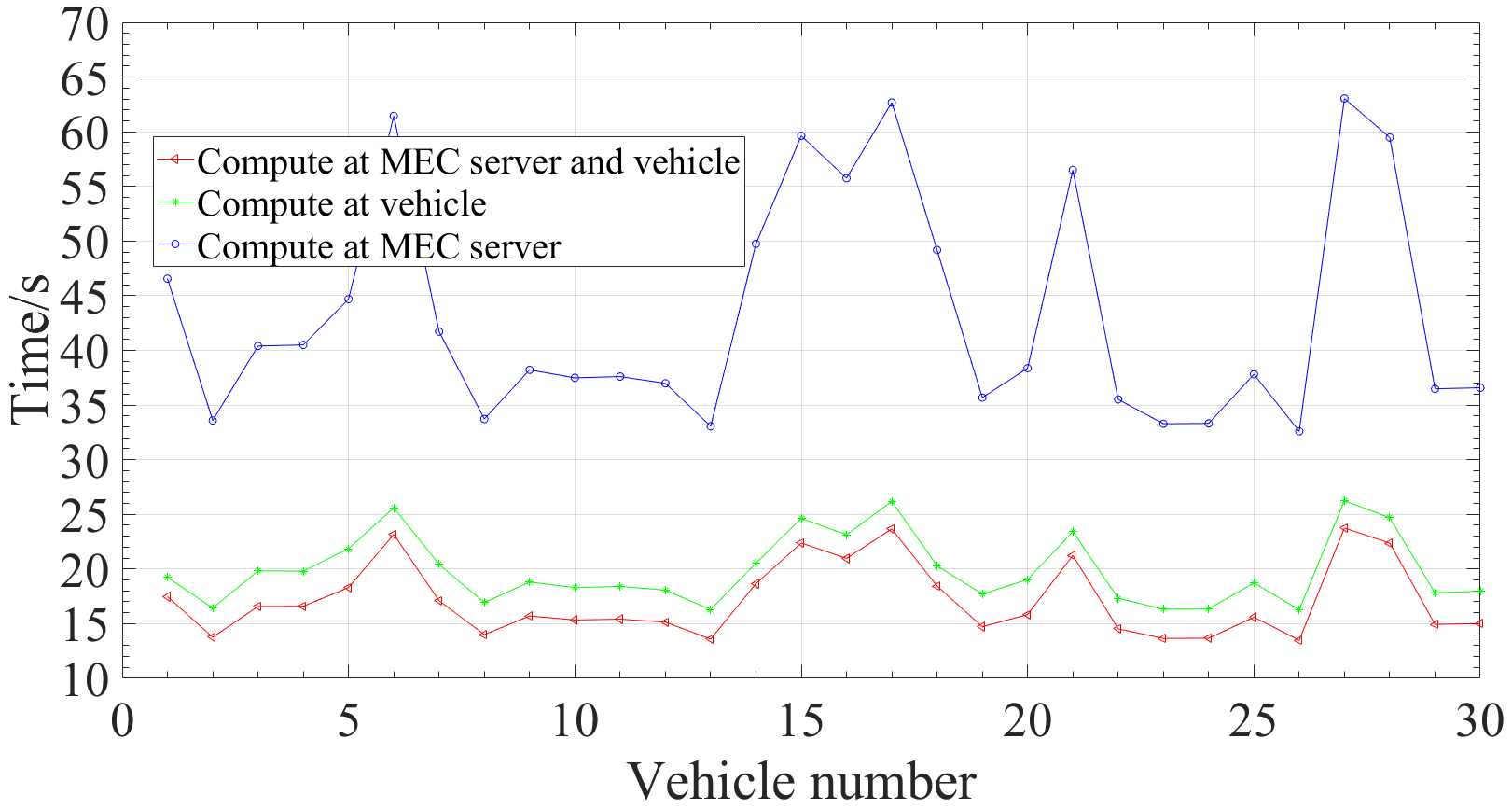
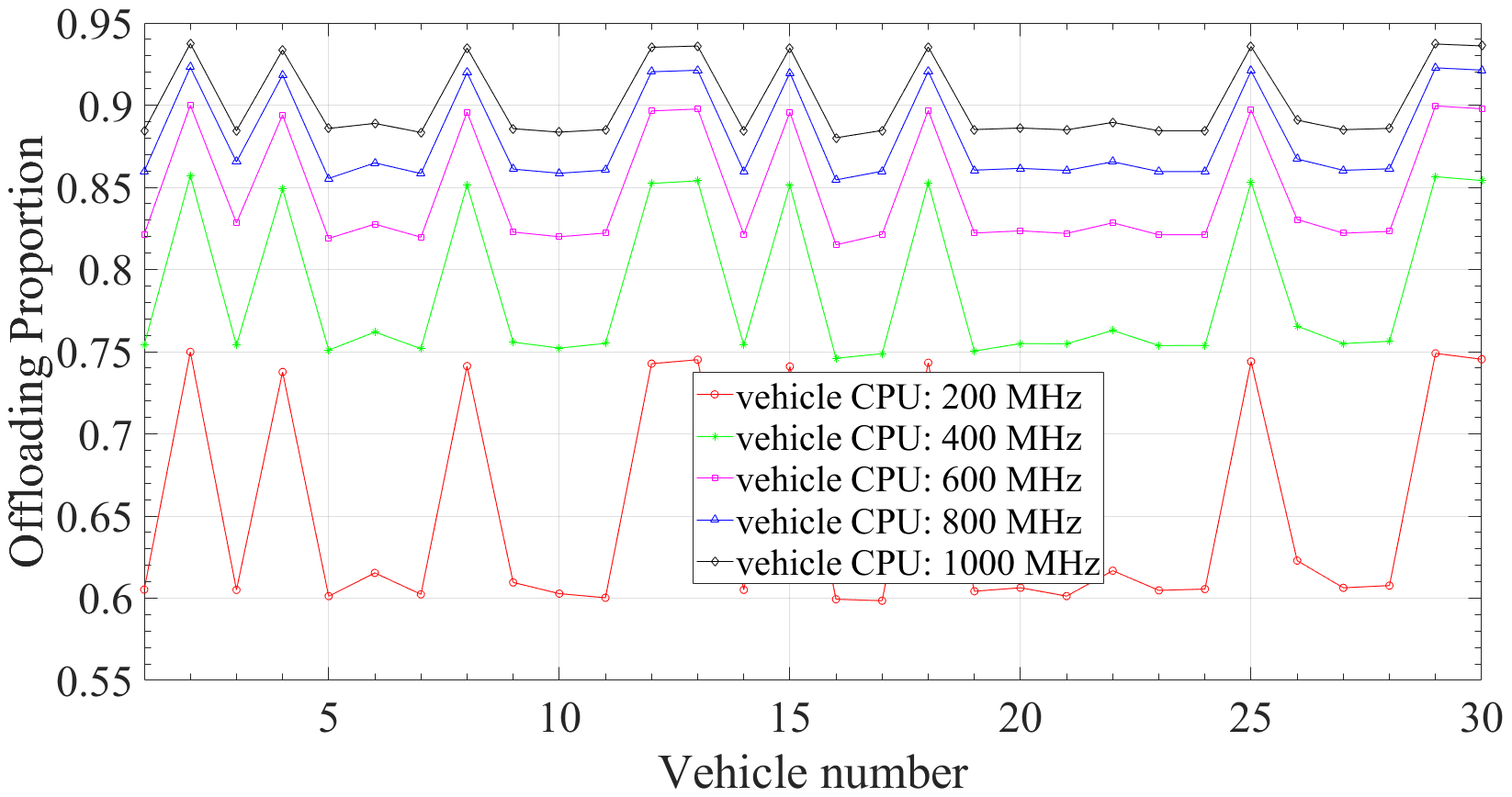
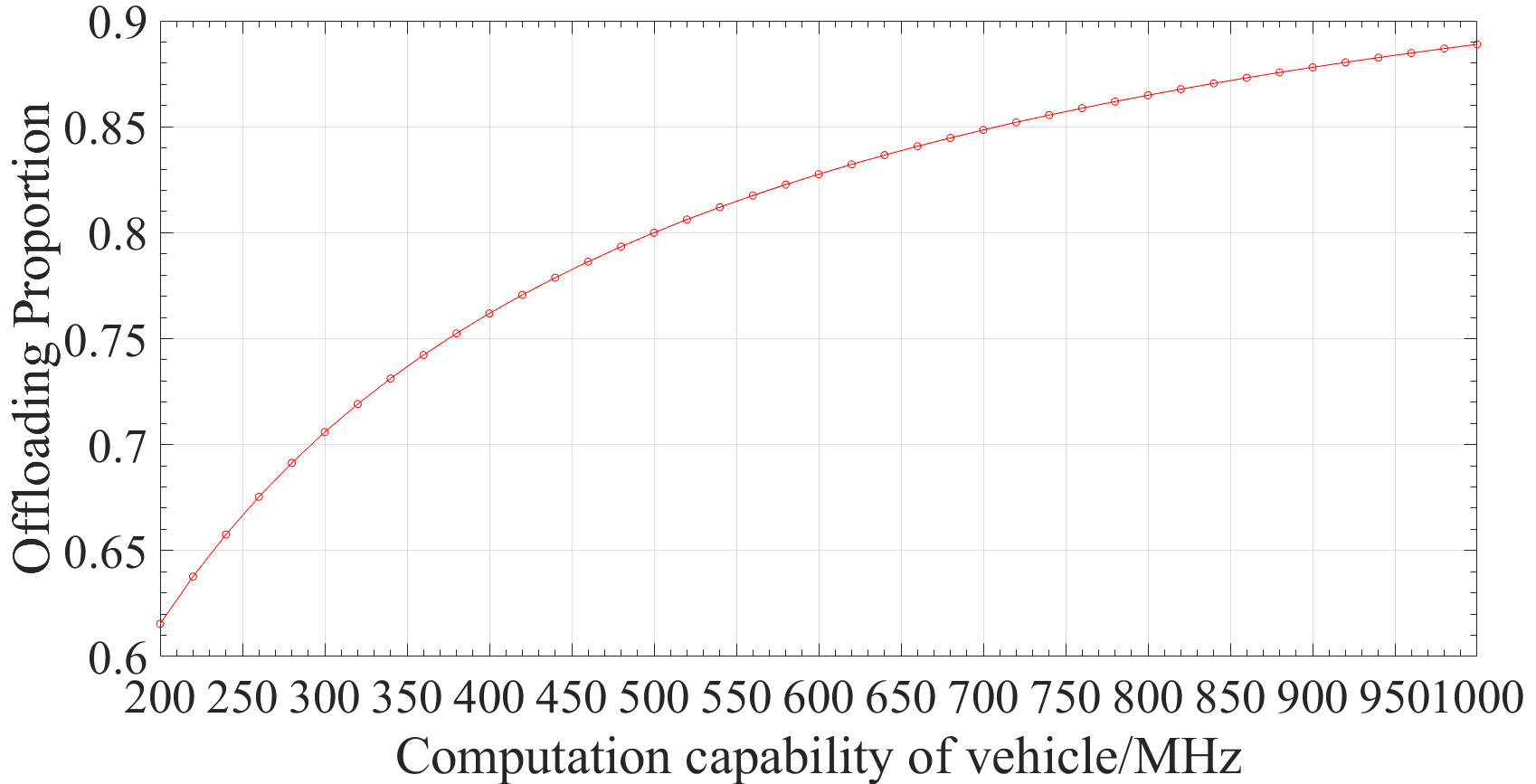
图4和图5展示了车辆计算能力对卸载比例的影响。如图所示，随着车辆计算能力的增加，卸载比例也随之增加。这是因为通过利用车辆计算能力，车辆可以处理更大比例的子任务，从而减少由于在MEC服务器上处理其他子任务产生的大量结果所导致的传输延迟。

然后，我们将通过将计算每比特所需的CPU周期从1设置到100（即1 ≤ φ ≤ 100），来研究任务计算复杂度对卸载比例的影响。从图6可以看出，随着任务计算复杂度 φ的增加，卸载比例下降。这意味着当计算复杂度 φ较大时，为了利用MEC服务器丰富的计算资源帮助车辆处理任务，卸载比例会变小。

最后，我们将任务输出与输入比设置为从1到3（即 1 ≤ β ≤ 3）。从图7可以看出，卸载比例随着任务输出与输入比的增加而增加 β。其原因是 β的增加导致子任务的数据量增加在MEC服务器处理后，这意味着将涉及更长的传输延迟。因此，当 β较大时，会在MEC服务器上处理更小的子任务，以减少通信时延。从图中可以看出，如果 β足够大，最优方案趋向于在车辆端处理整个任务。

VI. 结论

本文研究了配备移动边缘计算系统的车联网，重点关注降低VR任务完成时间的问题。为此，建立了联合优化模型，以获得最优的计算卸载比例、通信资源和计算资源分配。由于该问题是NP难的，基于该特性，我们提出了一种联合卸载比例与资源分配优化（JOPRAO）算法以获得最优解。随后，我们讨论了车辆计算能力、任务计算复杂度和任务输出与输入比对卸载比例的影响。仿真结果表明，所提出的方法能显著降低VR任务完成时间的时延。