FP32、FP16、TF32、BF16:
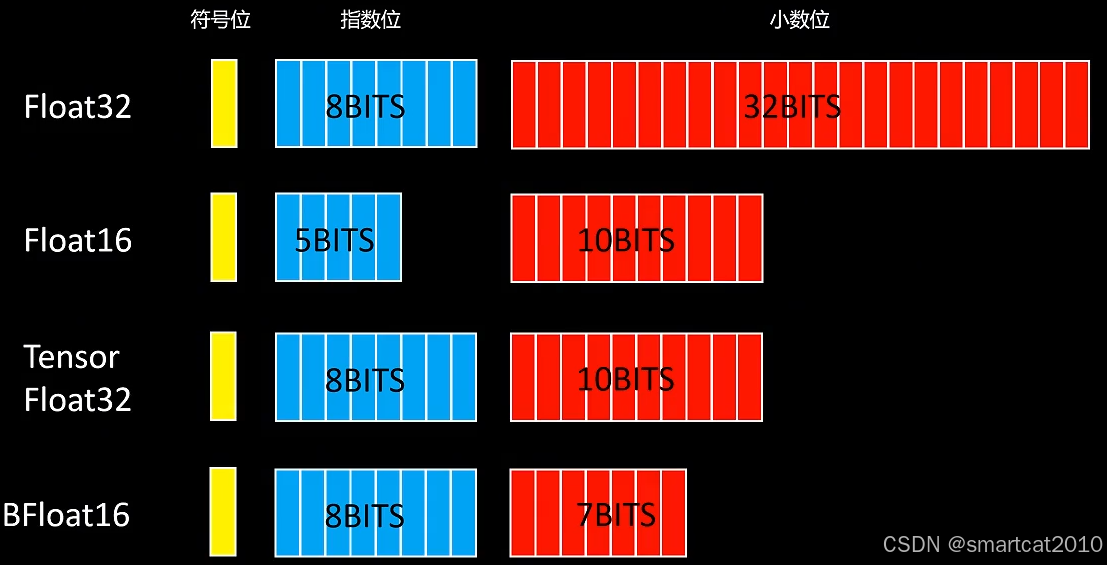
以FP16为例:
- 符号位: 1 位,0表示整数;1表示负数。
- 指数位:5位,范围为00001(1)到11110(30),正常来说整数范围就是 2^1~2^30 ,但其实为了指数位能够表示负数,引入了一个偏置值,偏置值是一个固定的数,它被加到实际的指数上,在二进制16位浮点数中,偏置值是 15。这个偏置值确保了指数位可以表示从-14到+15的范围即 2^−14~2^15 ,注:当指数位都为00000和11111时,它表示的是一种特殊情况,在IEEE 754标准中叫做非规范化情况。
- Fraction(尾数位):10位,简单地来说就是表示小数部分,存储的尾数位数为10位,但其隐含了首位的1,实际的尾数精度为11位,这里的隐含位可能有点难以理解,简单通俗来说,假设尾数部分为1001000000,为默认在其前面加一个1,最后变成1.1001000000(二进制)。
能表示的最大正数:
能表示的最小负数:同上, 只需要把符号位变成1,则为-65504
一般情况下,能表示的最小正数:
特殊情况下,即指数位全为0时,去掉开头隐含的首位1,可表示的最小整数:
如上,能表示的最大正数和最小正数,并不对称!最大约为2^15, 最小约为2^(-24)
FP16的好处,3条:
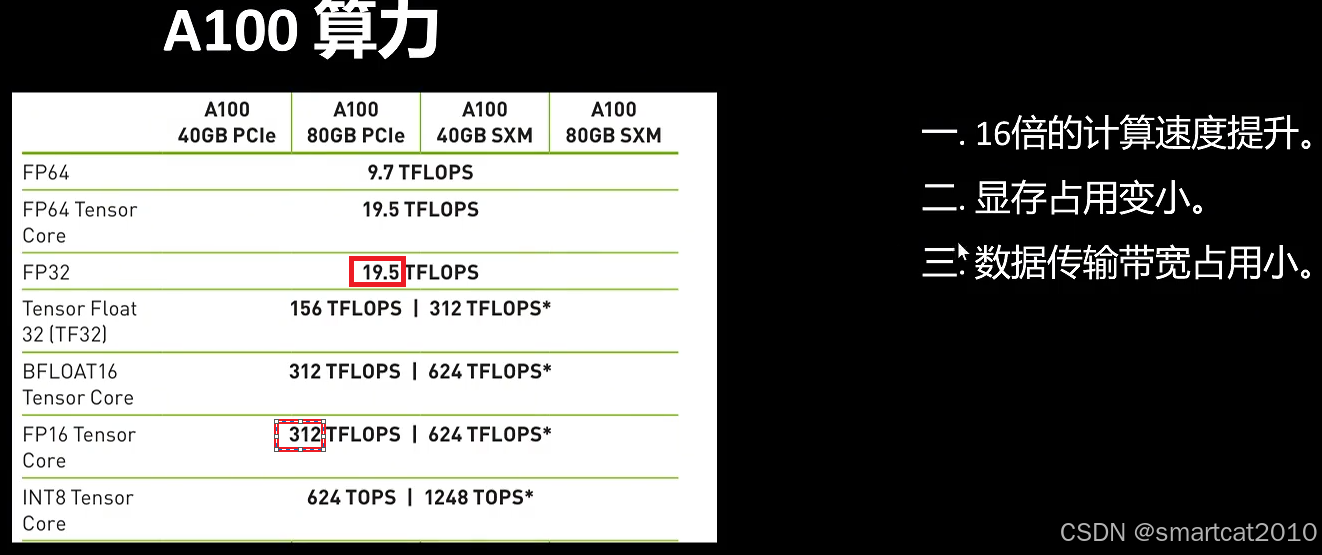
低精度带来的问题:
1. 表示范围问题
有些梯度太小,超出了FP16的最小正数(或最大负数)的范围,向下溢出,从而变成0。
2. 大数吃小数问题
大的数和小的数的加法,会先将小的数调整成指数等于大的数的指数,再对尾数相加。例如:
2048:
0.5:
调整成:
(超出了FP16的尾数长度,所以变成0了)
结果:2048+0.5=2048
更新权重时,梯度的范围分布:
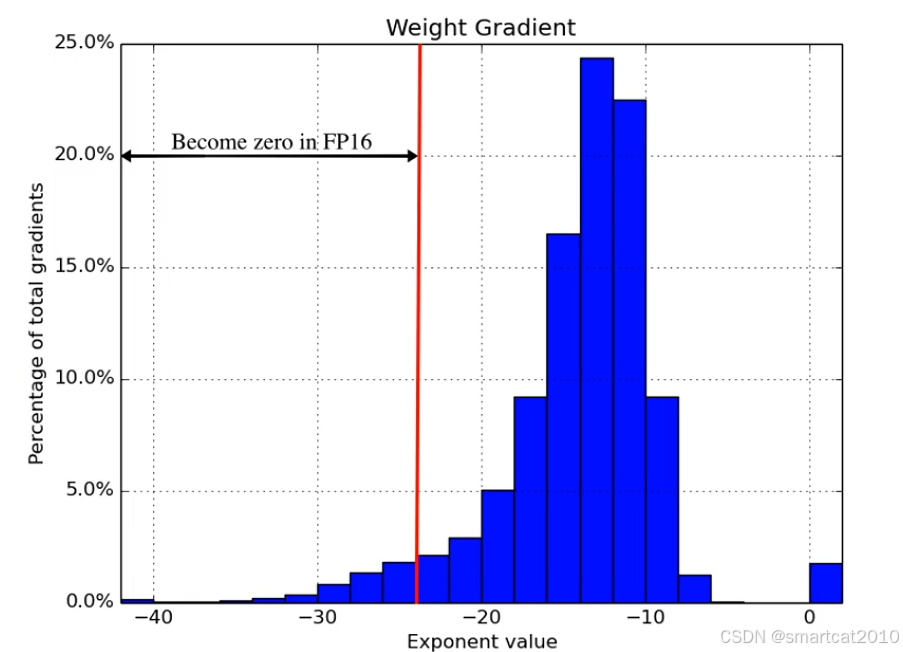
如上,有一部分梯度超出了2^(-24)的abs最小正数的范围,被视为0了。
解决大数吃小数问题:
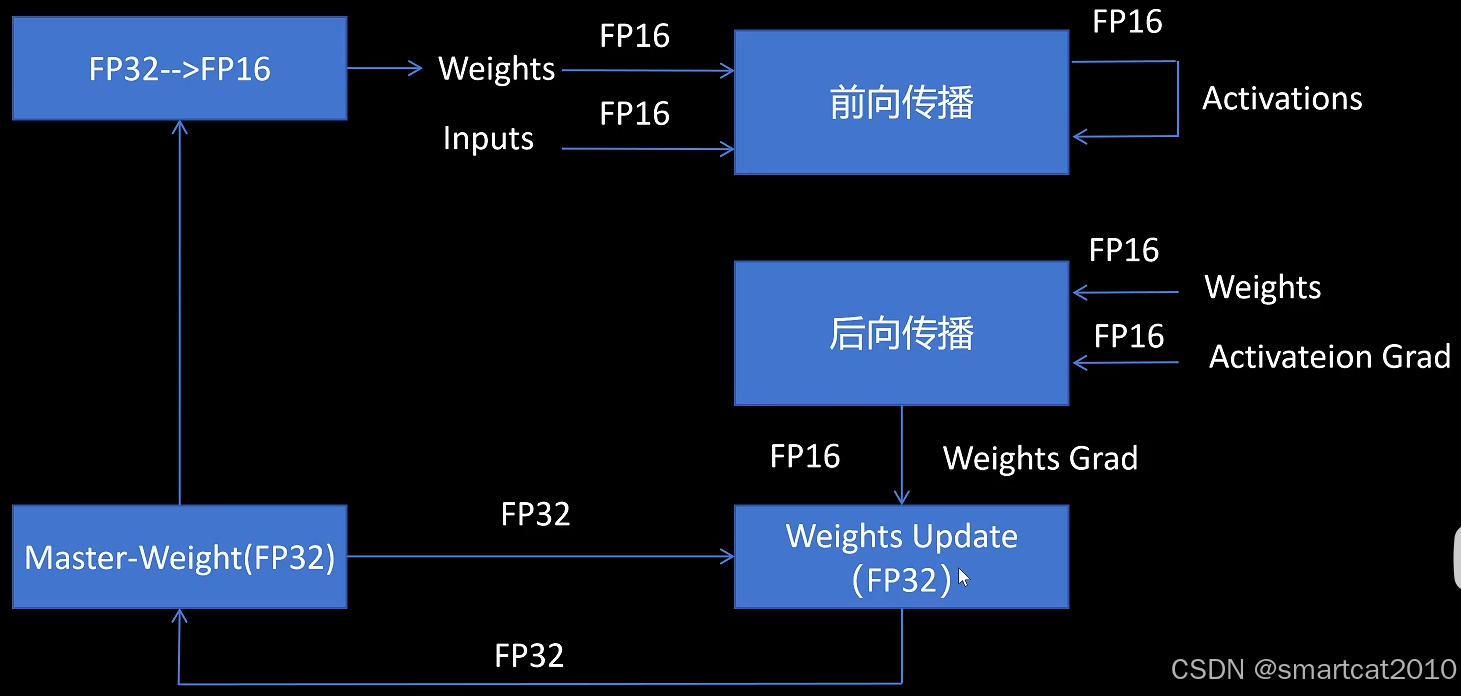
采用混合精度计算,流程:
Optimizer里,保存了一份FP32的Weight.
FP16的梯度,会先转成FP32,再和FP32的Weight进行计算,更新存入下一轮的FP32 Weight中。
FP16的梯度,转成FP32,再和FP32的Weight进行更新,就避免了大数吃小数的问题。
解决绝对值太小的数的下溢的问题:
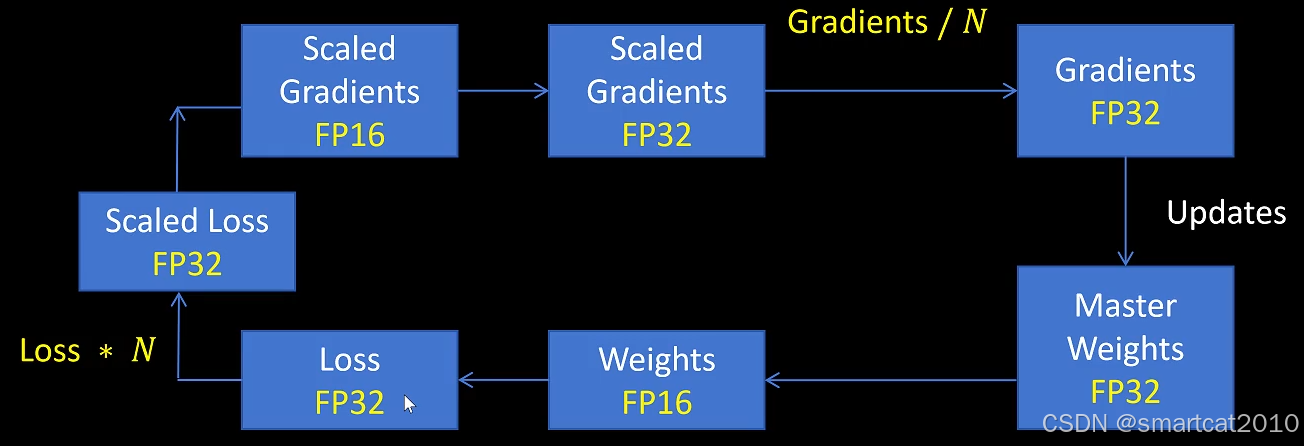
可以观察到,梯度在2^(-24)以下有一些,在2^15部分还有很多余量,因此,对梯度整体放大,可以避免梯度计算过程中的下溢,最后参数更新前再对梯度整体缩小回来。
注意:Loss计算使用FP32计算的,得到FP32的loss值。
对loss放大N倍,所以叫做Loss-Scaling。
PyTorch中,可以转为FP16和只能用FP32的ops:
FP32的op包括:计算loss、sum(加起来容易出现大数吃小数的问题)
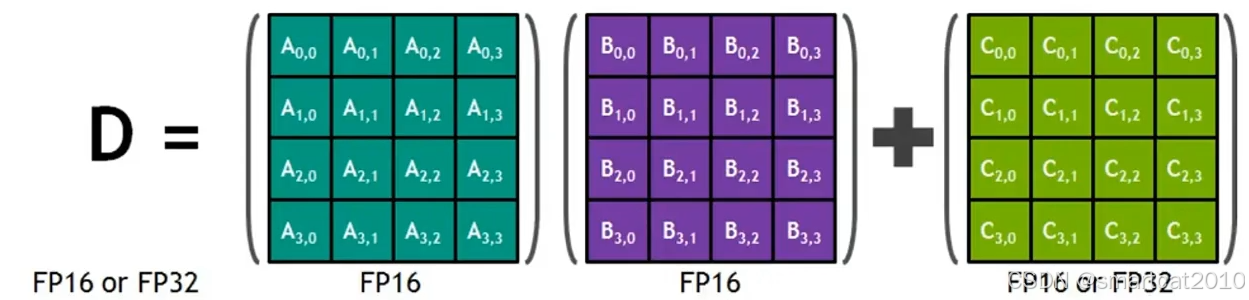
矩阵乘加的常用混合精度:
2个矩阵乘法,用FP16;乘完以后,转成FP32,去和另一个FP32矩阵相加,得到FP32的结果,最后可再转成FP16。
效果:
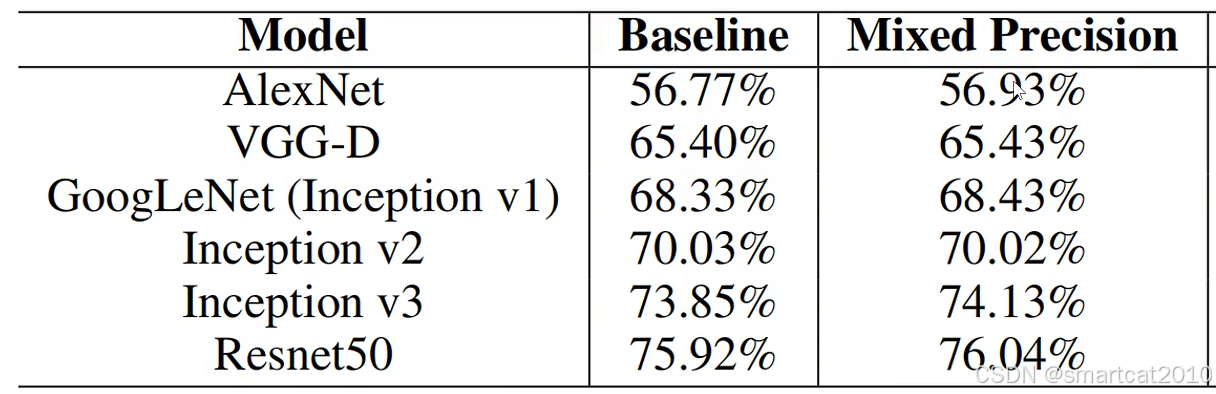
据说不影响效果。反而还能变好一点儿。
PyTorch混合精度计算和Loss-Scaling的代码:
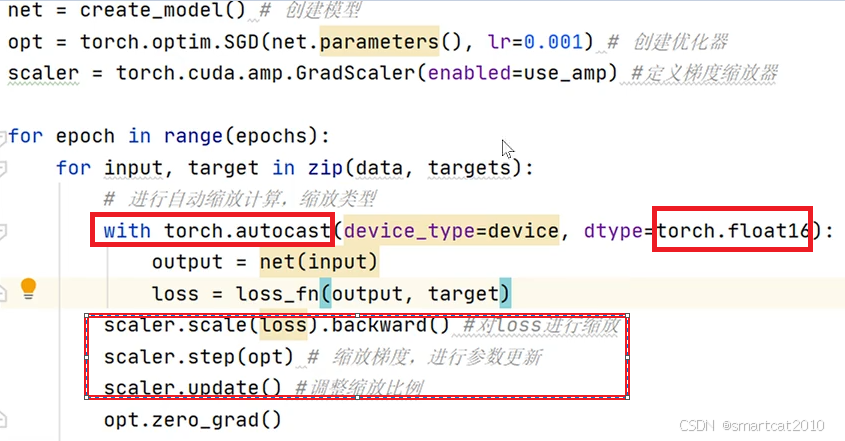







 本文探讨了混合精度训练在深度学习模型中的应用,通过使用半精度(FP16)与单精度(FP32)结合的方式,有效提升了模型训练速度与GPU内存利用率。文章介绍了NVIDIA与百度合作开发的技术,包括FP32主权重副本、损失缩放和BN处理等关键技巧,这些方法在保持模型精度的同时,显著减少了训练所需资源。
本文探讨了混合精度训练在深度学习模型中的应用,通过使用半精度(FP16)与单精度(FP32)结合的方式,有效提升了模型训练速度与GPU内存利用率。文章介绍了NVIDIA与百度合作开发的技术,包括FP32主权重副本、损失缩放和BN处理等关键技巧,这些方法在保持模型精度的同时,显著减少了训练所需资源。

















 760
760

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








