leetcode----131. Palindrome Partitioning

最新推荐文章于 2025-08-08 11:49:43 发布

成程晨

最新推荐文章于 2025-08-08 11:49:43 发布

阅读量108

点赞数

CC 4.0 BY-SA版权

分类专栏： leetcode 文章标签： leetcode 回溯

本文链接：https://blog.youkuaiyun.com/smart_ferry/article/details/89328211

leetcode 专栏收录该内容

101 篇文章

订阅专栏

本文介绍了一种解决LeetCode回文串分割问题的方法，通过构建二维布尔数组判断子串是否为回文，再利用回溯法求解所有可能的分割方案。代码示例清晰展示了算法设计思路。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

链接：

https://leetcode.com/problems/palindrome-partitioning/

大意：

给定一个字符串s，要求给出s的所有切分情况，使得切分后的每个子串都是回文串。例子：

思路：

记录一个二维boolean数组p，p[i][j]意为s.substring(i, j + 1)是否为回文串。

接下来就是基于上一步求得的boolean数组p使用回溯法了。

具体思路看代码。

代码：

class Solution {
    public List<List<String>> partition(String s) {
        List<List<String>> res = new ArrayList<>();
        if (s.length() == 0)
            return res;
        int len = s.length();
        boolean[][] p = new boolean[len][len]; // p[i][j]:s.substring(i, j + 1)是否为回文串
        for (int i = 0; i < len; i++) {
            for (int j = i; j < len; j++) {
                if (isPalindrome(s, i, j))
                    p[i][j] = true;
            }
        }
        dfs(s, p, 0, len, new ArrayList<>(), res);
        return res;
    }
    // r为当前的p为第几行 从0开始
    public void dfs(String s, boolean[][] p, int r, int len, List<String> list, List<List<String>> res) {
        int i = r;
        while (i < len) {
            if (p[r][i]) {
                // 找到一组分割
                if (i == len - 1) {
                    res.add(new ArrayList<>(list));
                    res.get(res.size() - 1).add(s.substring(r, i + 1));
                    return ;
                }
                list.add(s.substring(r, i + 1));
                dfs(s, p, i + 1, len, list, res); // s.substring(r, i + 1)为回文串 则下一个可能的回文串起始位置从 i + 1 开始
                list.remove(list.size() - 1); // 回溯
            }
            i++;
        }
    }
    // 判断s从start到end(含)是否为回文串
    public boolean isPalindrome(String s, int start, int end) {
        while (start < end) {
            if (s.charAt(start) != s.charAt(end))
                return false;
            start++;
            end--;
        }
        return true;
    }
}

结果：

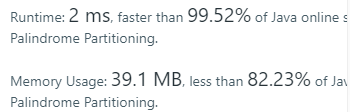
结论：

享受AC带来的快感，感觉现在做题越来越有算法设计的意思了...

四个月后再刷：

class Solution {
    public List<List<String>> partition(String s) {
        List<List<String>> res = new ArrayList<>();
        dfs(s.toCharArray(), 0, res, new LinkedList<String>());
        return res;
    }
    // 含左不含右
    public void dfs(char[] array, int left, List<List<String>> res, LinkedList<String> list) {
        if (left == array.length) {
            res.add(new ArrayList<>(list));
        }
        for (int right = left + 1; right <= array.length; right++) {
            if (isHuiWen(array, left, right)) {
                list.addLast(new String(array, left, right - left));// 三个参数: char[] offset count
                dfs(array, right, res, list);
                list.removeLast(); // 回溯
            }
        }
    }
    public boolean isHuiWen(char[] array, int left, int right) {
        while (left < right) {
            if (array[left++] != array[--right])
                return false;
        }
        return true;
    }
}