ML第一节课，汇总

一、Machine learning algorithms（3种）

• supervised learning
• unsupervised learning
• reinforcement learning (应用较少)

1. 什么是有监督学习和无监督学习

有监督学习和无监督学习一字之差，关键在于是否有监督，也就是数据是否有标签。

2. 有监督学习（有标签）

• 监督学习的主要目标是利用一组带标签的数据，学习从输入到输出的映射，然后将这种映射关系应用到未知数据上，达到分类或者回归的目的。
  

• 主要分为两类：回归（regression）和分类（classification）

2.1 回归 regression

• 用来预测number的，从无限多种可能性的结果中预测。如：预测房价…

2.2 分类 classification

• 用来预测categories，从一小组有限的可能性结果中预测。如：良性/恶性1型/恶性2型，0/1， cat/dog…
  

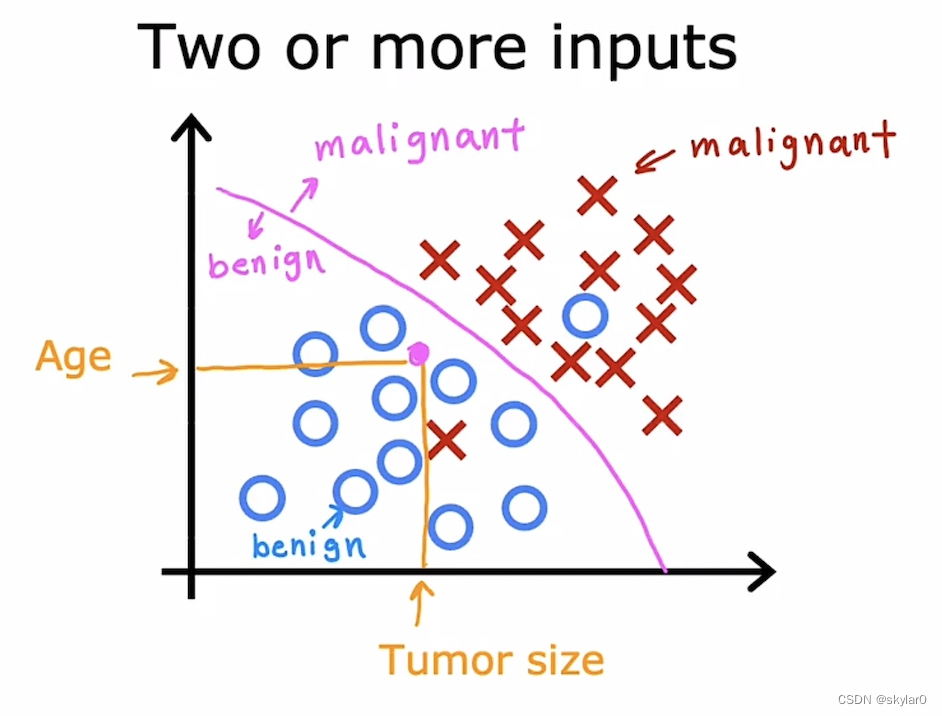
3.无监督学习（无标签）

• 不依赖任何标签值，通过对数据内在特征的挖掘，找到样本间的关系，如聚类、降维。
• 数据通常只跟随x input，没有y输出值的label。算法需要自己去找出data的structure。
  【没有标签的，需要机器自己去将数据分类】
• 主要分成2种：聚类和降维。

3.1 聚类算法 clustering algorithm

• 聚类问题：将相似的data分到同一组去。
• 如：百度搜索时，会将跟关键词有关的数据都显示出来。

3.2 异常值检测anomaly detection

• 找出unusual data points。
• 在金融系统的欺诈检测很有用。

3.3 降维 dimensionality reduction

• compress data只使用fewer number。

二. 线性回归模型（最广泛）

1. 房价预测的例子

1. 线性回归： 预测出一条straight line，然后根据size预测price。
2. 数据的呈现也可以是右边这个形式。

3. training set训练集：给定的数据集。（如图）
4. 为了测试机器学习算法的效果，通常使用两套独立的样本集：训练集和测试集。当机器学习程序开始运行时，使用训练集作为算法的输入，训练完成之后的那个东西叫模型，我们可以借助模型，通过输入测试集来预测目标变量。比较预测出来的目标变量和实际目标变量之间的差别，就可以算出算法的实际精确度。
5. standard notation： I表示第I个训练例子。表示的index。

1.1 linear regression模型

2. 例子：房子size-----f------price（prediction）
3. 如何找到function f：
   a. 通过linear regression找到function f(x)

2. cost function

1. w,b是parameter，coefficients，weight

2. w,b的变化会影响f(x)的值和对应的图像。

2.1 cost function公式

2.2 cost function理解

1. model：f(x)=wx+b
2. parameter: w,b
3. cost function:

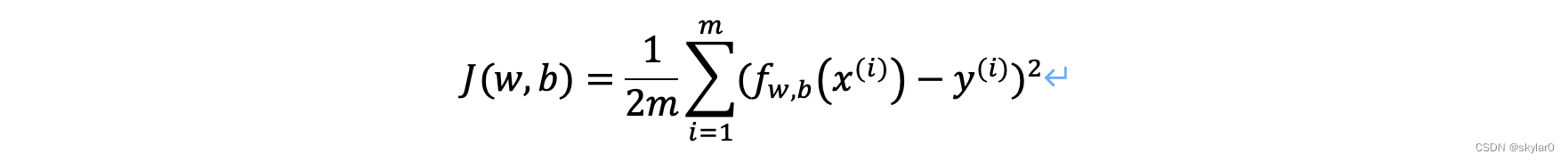
4. goal: minimize J(w,b)
5. 如何实现J(w,b)最小化(3点)：
   a. 通过f(x)—>J(w)：假设b=0，固定w=1，找到f(x)的值以及通过f(x)的值找到对应的J(w)
   b. 变化w的值，找出J(w)的图像
   c. 通过J(w)的图像找出最小值，从而实现minimize J(w).
   
   

2.3 cost function 可视化

【不忽略b的话】

1. J(w)的3D图像：

2. 将3D图像2D化：使用等高线概念
   a. 同一条线上的J(w)值相同。
   b. 等高线图的中心点为最低点minimize。

3. 可视化举例（3个例子）

• 1. J(w)图上，点w=-0.15 b=800【J(w)值很大】对应的straight line是左图这样的。可以看出是非常不合适的straight line。误差很大。

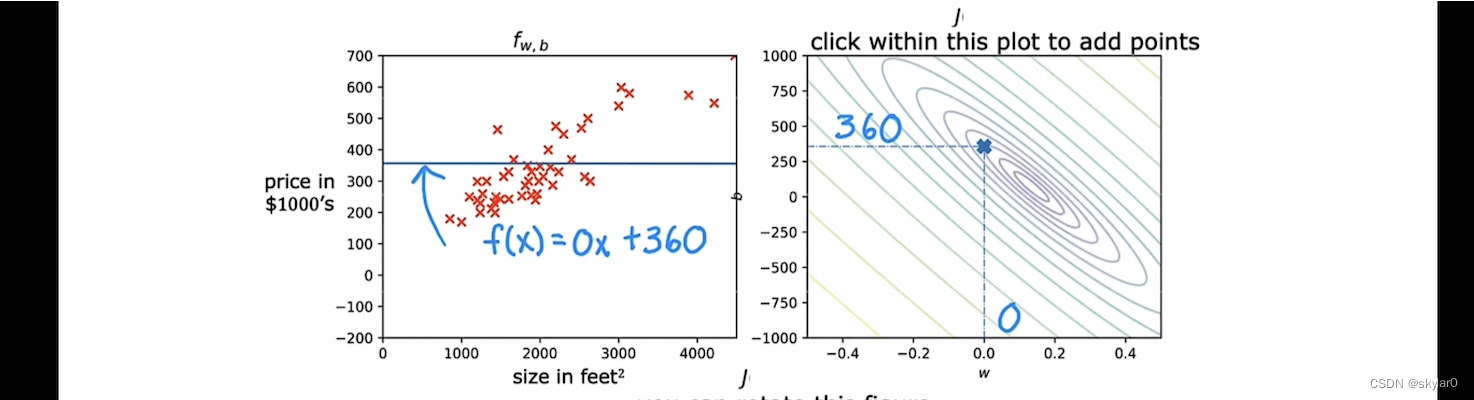
• 2. J(w)图上，点w=0 b=360【J(w)值相对小一点】对应的straight line是左图这样的。可以看出是这条straight line也不太合适。误差相对较大，但比上一个例子好一点。

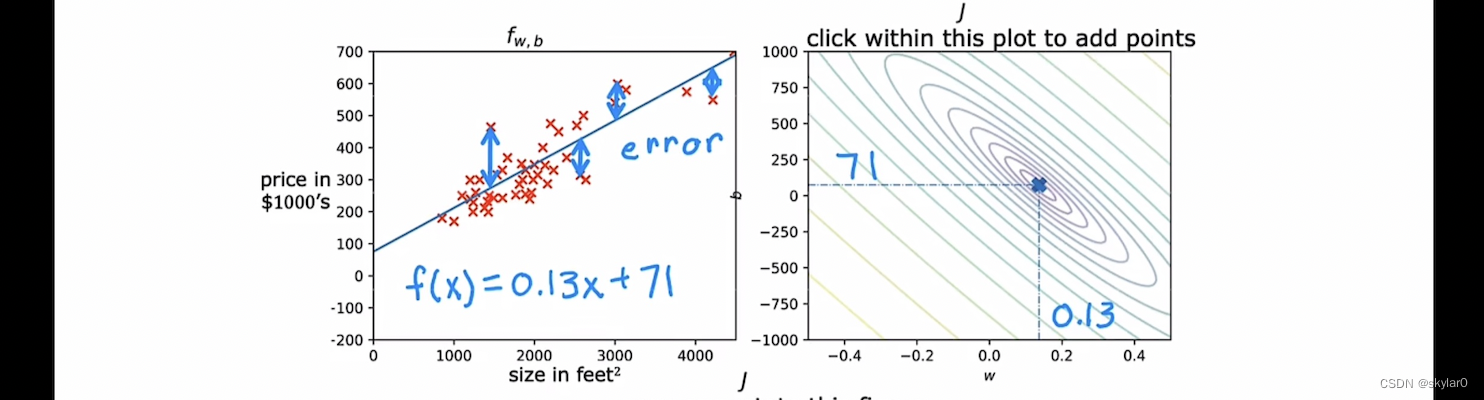
• 3. J(w)图上，点w=0.13 b=71【J(w)值很小】对应的straight line是左图这样的。可以看出是比较合适的straight line。误差很小。

三. 梯度下降Gradient Descent（找到minimum J（w）的好方法）

1. 梯度下降概念

1. 用来找到w，b，在J(w)最小的时候。
2. 代价函数J(w,b)，我们想要最小化代价函数。
3. outline：
   1. start with some w，b。通常set w = 0，b = 0
   2. 不断变化w，b的值去降低J(w,b)。
   3. until 我们找到or 靠近minimum（注意：J(w,b)函数不一定是u型/碗状的，minimum可能不止一个。）
      

2. 梯度下降的实现

2.1 梯度下降的算法

1. 公式：

• α: learning rate, 范围[0,1]。如果α很大，则梯度下降很快。

2. 同时更新w，b的值。
   

3. 理解梯度下降（derivative的重要性）

1. 假设只有一个参数w，例1显示斜率 > 0，derivative > 0，w会左移，更接近minimize w。
2. 假设只有一个参数w，例2显示斜率 < 0，derivative < 0，w会右移，更接近minimize w。
   

4. 学习率learning rate

1. α太小，gradient descent会很慢。
2. α太大，gradient descent有可能oveershoot，错过minimum，导致J(w)反而变大。—> diverge离散

3. 如果w已经在J(w)的local minimum了，derivative = 0，则w会不变。
   【当w不变时，则到达了J(w)的local minimum】
4. 即使α不变，当接近local minimum的时候，会自动采取更小的步骤接近他。因为derivative（斜率）在变小，所以steps会变小。
   

5. 线性回归的梯度下降

3. 对于linear regression来说(它的特性)，找到的minimum一定是globle minimum。

6. 实例

1. 从w=-0.1，b=900开始，f(x)=-0.1x+900
   实现梯度下降的过程：

2. “Batch” gradient descent：批量梯度下降

• “Batch”gradient descent每一步都会使用所有的training examples。

四、 multiple linear regression多元线性回归

1. 多维特征 Multiple features

1. xj = 第j个feature
2. n = feature的个数
3. x ⃗^(i) = 第（i）个training example的features。（行向量row vector）
4. (x_j ) ⃗^(i) = 第（i）个training example的第j个feature的值。
   如： x_3^2 = 第3个training example的第2个feature = 3

5. model：

• w ⃗ = [w1, w2, …wn] 是parameter of the model
• b 是一个常数
• x ⃗ = [x1, x2, x3, … xn]
  

6. multiple linear regression（不是multivariate regression）
   

2. 向量化 vectorization

1. 不使用dot product一个一个乘积相加，如果n很大的时候，非常耗时。
2. 不实用dot product，使用for loop可以提升效率，但还不够
3. dot product会提升代码效率，只需要一行。

f = np.dot(w,x) + b

4. 是否使用vectorization的效率差别：

3. 多元线性回归的梯度下降

1. notation的不同：

4. normal equation正规方程

1. 定义：
   （1）只适用于linear regression
   （2）不需要iterations，解决w，b的值。
2. 缺点：
   （1）这个在其他算法不适用。
   （2）会很慢，如果features很大（n > 10,000）
3. 有些机器学习库会在后端back-end解决w和b。
4. 对于找到parameter w和b的问题，还是推荐使用gradient descent梯度下降。

五、 Feature Scaling特征缩放

1. feature scaling：

可以让gradient descent运行的更快。

1.1 确认feature和对应的parameter的值：

• 当feature的范围比较大的时候，它对应的parameter值应该比较小。

1.2 rescale的原因

• 如图，parameter取值像上图一样，我们做gradient descent时会很慢。通过rescaling可以让cost function接近圆形，使得gradient descent更加的快捷。

1.3 rescaling的3种方式：

• feature scaling-- [0,1]
• mean normalization
• z-score normalization
  

1.4 总结：范围太大/小都需要rescale。

2.判断梯度下降是否收敛

1. 一个适当的alpha，会使得在每一个iteration之后，J(w,b)都会下降。
2. 如果J(w,b)上升，证明alpha选的不合适。
3. J(w,b) 在400次iteration之后，learning curve开始趋于水平。这意味着，J(w,b)很可能converged by 400 iterations。
4. 自动收敛检测automatic convergence test：如果每一个iteration后，J(w,b)的值下降的非常小（<=epsilon），则可以说他convergence了。

3.如何设置学习率

1. 如果J(w,b) 时上时下 / 持续上升，要么有code错误，要么alpha太大了。
2. 先将alpha设置为一个非常小的数，看一下J(w,b) 是不是在每一个iteration后都下降。如果不下降，则code有错误。
3. 但如果alpha设置的太小了，要找到convergence要很久。
4. 从很小的alpha开始，J(w,b)持续下降，则缓慢提高alpha。

4.特征工程

1. 定义： 使用直觉，去设计一个新的feature，通过转移/结合原有的features。
2. 找到最合适的features：
   

5. 多项式回归

1. 可以选择x^2 / x^ 3 / x^ 0.5
   

六、classification

1. binary classification

1.预测结果为true / false。需要logistic算法来完成预测。

2. logistic regression （预测类型）

2. 1 阈值threshold

相当于一条边界线，大于这个边界线是一个结果，小于这个边界线则是另一个结果。在logistic regression里，> 边界线就是1，< 边界线就是0。

2.2 sigmoid function(logistic function):

• 如：treshold=0.7，则x>0.7时，y=1。x<0.7时，y=0。
• 右边的threshold=0.5（通过z=0算出来的）
  

2.3 公式：

2.4 理解：

• 逻辑函数相当于某个output发生的probability。
  如：f（x）=0.7意思是70%的可能性y=1。
  

3. decision boundary决策边界

1. 找boundary在z=0的时候：
   
   

七、logistic regression的cost function和gradient descent

1. 逻辑函数的cost function

1. 回归，已知这个training set怎么找到最合适的w和b。

2. Squared error cost function在linear和logistic下的对比。在logistic regression下他不是convex的，有非常多的local minimum。

---

1.1 logistic loss function

1. 如果y = 1。
2. -log函数是左图蓝色线。因为y = 1 / 0，所以粉色框架内为有效区域。
3. 放大这个区域，当预测值f(x) --> 1， loss --> 0。f(x) --> 0, loss --> ∞。
4. 当预测值f(x)最接近真实值y，损失最小。

4. 如果y = 0。

5. 函数图像如图，放大来看可知。预测值f(x) --> 1， loss --> ∞。f(x) --> 0, loss --> 0。
   

6. logistic regression的新代价函数是可以convex的，有global minimum。

---

#3# 1.2 simplified cost function

1. 简化的loss公式：

2. 简化的cost公式：
   

---

2. 梯度下降gradient descent

• 会不会疑惑这个和linear regression的梯度下降很像。但因为f(x)是不一样的，所以cost function也会不一样。

八、 过度拟合

1.三种预测的情况：

1.1 underfit

• 有很高的bias
• 并不能很好的fit我们的training set

1.2 generalization

• 可以很好的预测不在training set里的数据。

1.3 overfit

• cost 几乎等于0
• 无法推广
• 算法有high variance高方差（overfit的另一种术语）。完全fit training set，如果有一个training set 稍微有点不同就会得到完全不同的预测。

---

1.4 对于classification也一样

---

2. 如何解决过度拟合（3种）

1. 收集更多的training set
2. 选择更合适的feature（x）（减少/增加）
3. regularization： 减小parameter的size。
   （1）保留所有的feature但要防止feature产生过大的影响。
   （2）b不需要regularization，b的变化几乎不影响。

3. regularization

1. lambda：regularization parameter，lambda > 0。
2. 使用第一个term来fit data。
3. 使用第二个term来minimize w。

4. 如何选择lambda：

• =0 ： f(x) = b
• 太大：f(x) overfit

3.1 用于linear regression的regularization

• 偏导后面有过程。
  

• 重新排序wj。前一项非常接近 wj。

• 正规项求偏导：最后等于lambda * wj / m，求和项展开，只有wj项会保留。

3.2 用于logistic regression的regularization

• 加上regularization term会使得预测的曲线更加的平滑，避免overfit

• 注意：b 不做regularization。