线性回归---7,正则化的线性模型

Ridge Regression 岭回归
Lasso 回归
Elastic Net 弹性网络
Early stopping
1 Ridge Regression (岭回归，又名 岭回归是线性回归的正则化版本，即在原来的线性回归的 cost function 中添加正则项（regularization term）: Tikhonov regularization)

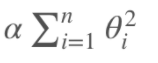
以达到在拟合数据的同时，使模型权重尽可能小的目的,岭回归代价函数

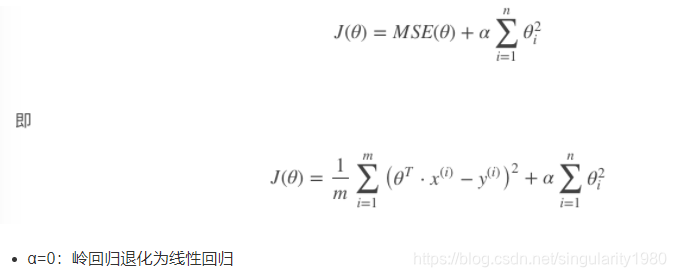
2 Lasso Regression(Lasso 回归)
Lasso 回归是线性回归的另一种正则化版本，正则项为权值向量的ℓ1范数。

Lasso回归的代价函数 ：

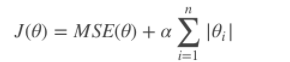
【注意 】

Lasso Regression 的代价函数在 θi=0处是不可导的.
解决方法：在θi=0处用一个次梯度向量(subgradient vector)代替梯度，如下式
Lasso Regression 的次梯度向量
image-20190404181709725

Lasso Regression 有一个很重要的性质是：倾向于完全消除不重要的权重。

例如：当α 取值相对较大时，高阶多项式退化为二次甚至是线性：高阶多项式特征的权重被置为0。

也就是说，Lasso Regression 能够自动进行特征选择，并输出一个稀疏模型（只有少数特征的权重是非零的）。
3 Elastic Net (弹性网络)
弹性网络在岭回归和Lasso回归中进行了折中，通过 混合比(mix ratio) r 进行控制：

r=0：弹性网络变为岭回归
r=1：弹性网络便为Lasso回归
弹性网络的代价函数 ：

image-20190406110447953

一般来说，我们应避免使用朴素线性回归，而应对模型进行一定的正则化处理，那如何选择正则化方法呢？

小结：

常用：岭回归

假设只有少部分特征是有用的：

弹性网络
Lasso
一般来说，弹性网络的使用更为广泛。因为在特征维度高于训练样本数，或者特征是强相关的情况下，Lasso回归的表现不太稳定。
api:

from sklearn.linear_model import Ridge, ElasticNet, Lasso