线性回归---4.线性回归的损失和优化

最新推荐文章于 2024-10-13 23:16:35 发布
原创 最新推荐文章于 2024-10-13 23:16:35 发布 · 1.4k 阅读 · 0 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文介绍了线性回归中的损失函数，重点讨论了最小二乘法和优化过程。通过正规方程与梯度下降两种方式解释了如何寻找最佳参数，其中梯度下降利用函数的梯度方向指导参数更新，以达到损失函数最小化的目标。

1.什么是损失
真是值和预测值之间的误差
公式:最小二乘法

在这里插入图片描述
2.如何进行优化
第一种方法 正规方程
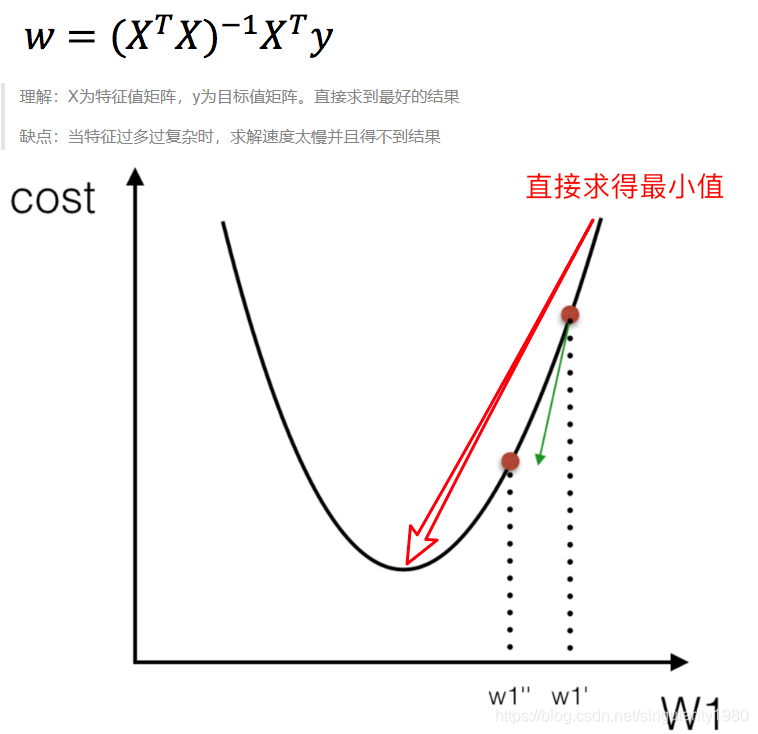
在这里插入图片描述
举例
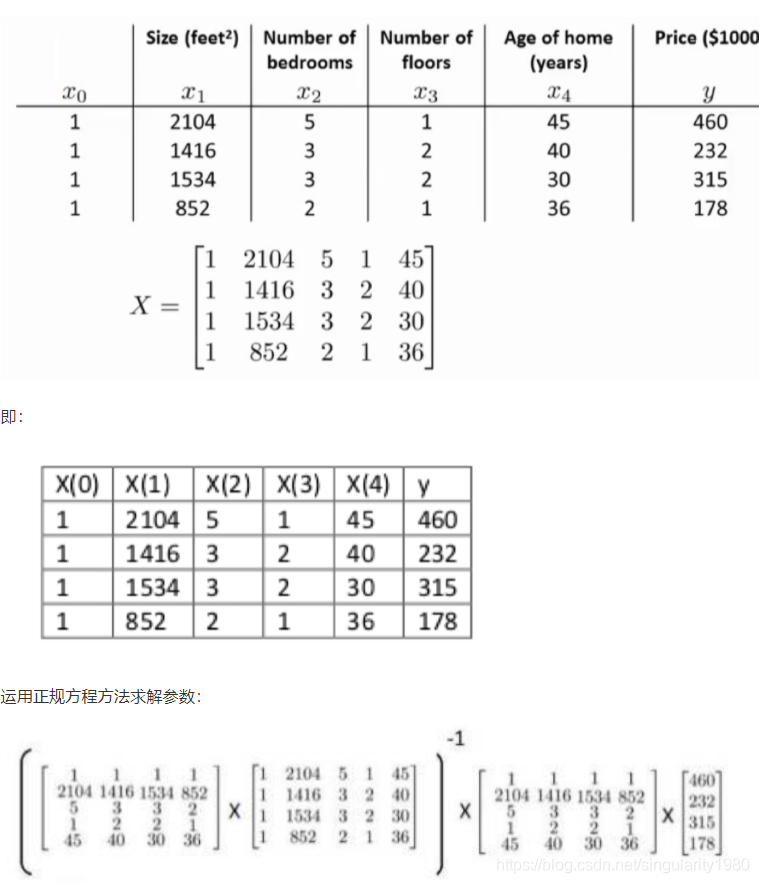
在这里插入图片描述
详解:
1.特征值逆矩阵 乘 特征值原矩阵 乘 特征值逆矩阵 * 目标值矩阵 T 就是矩阵转置 -1就是逆矩阵

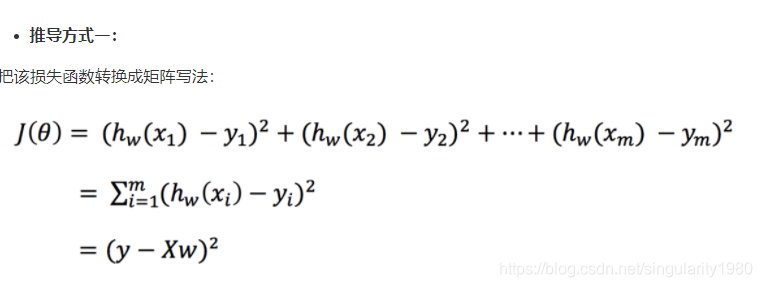
在这里插入图片描述
在这里插入图片描述
第二种方法 梯度下降

概念

梯度是微积分中一个很重要的概念

​ 在单变量的函数中，梯度其实就是函数的微分，代表着函数在某个给定点的切线的斜率

​ 在多变量函数中，梯度是一个向量，向量有方向，梯度的方向就指出了函数在给定点的上升最快的方向

这也就说明了为什么我们需要千方百计的求取梯度！我们需要到达山底，就需要在每一步观测到此时最陡峭的地方，梯度就恰巧告诉了我们这个方向。梯度的方向是函数在给定点上升最快的方向，那么梯度的反方向就是函数在给定点下降最快的方向，这正是我们所需要的。所以我们只要沿着梯度的反方向一直走，就能走到局部的最低点！

单变量梯度下降

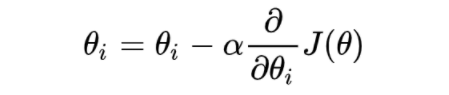
在这里插入图片描述
多变量梯度下降
在这里插入图片描述
梯度下降的公式

在这里插入图片描述

人工智能类比赛从入门到精通 一
qq_39903036的博客
11-02 790
入门实战级比赛一前言1、赛题解读2、相关知识点2.1二分类问题2.1.1分类回归相关概念2.1.2 二分类评价指标2.1.3 二分类算法2.2 逻辑回归2.2.1 线性回归2.2.2 逻辑回归实战演练 前言 本篇文章是先进行赛题解读，然后介绍相关知识点，最后进行实战演练，此实战代码完全可应用到企业内部使用～ 1、赛题解读 本次进行的比赛是一个预测分析比赛，预测客户的购买行为，即银行的客服人员与客户进行至少一次的电话联系，以确认客户是否有意愿购买该银行的产品。 此次比赛的基本类型是分类任务，即预测客户是否购买
深度学习笔记4：线性回归+基础优化方法
qq_49407329的博客
08-17 742
学习李沐老师的深度学习（pytorch），做的笔记4（视频8）~~~
线性回归问题优化
qq_43983010的博客
12-01 506
线性回归问题优化多元线性回归假设函数代价函数梯度下降算法特征缩放前言一、pandas是什么？二、使用步骤1.引入库2.读入数据总结学习目标：学习内容：学习时间：学习产出： 多元线性回归 在回归分析中，如果有两个或两个以上的自变量，就称为多元回归。 假设函数 当有多个特征量时我们的假设函数就变成了： 这里可以用矩阵向量的方法来对其进行简化： 而最终假设函数的表示方法就变成了： 代价函数 代价函数的表示就变成了： 代价函数的θ已经变成了一个向量 梯度下降算法 依次更新各个θ的值 特征缩放 提示：这
线性回归模型损失和优化
一步一脚印
11-12 1955
性回归模型损失和优化学习任务优化方法正规方程正规方程推导过程梯度下降梯度下降公式两者的对比如何选择小规模数据大规模数据 学习任务 使用正规方程对损失函数优化的过程 使用梯度下降法对损失函数优化的过程 优化方法 正规方程 正规方程,一次就可以求得最合适的值 理解：X为特征矩阵，y为目标值矩阵。直接求得最好的结果 缺点：当特征值过多复杂时，求解速度太慢并且得不到结果。 正规方程推导过程 梯度下降      梯度是微积分中一个很重要的概念，在单变量的函数中，梯度
深度学习优化函数详解（0）-- 线性回归问题
ChasingdreamLY的博客
03-24 1338
深度学习优化函数详解系列目录 深度学习优化函数详解（0）– 线性回归问题 深度学习优化函数详解（1）– Gradient Descent 梯度下降法 深度学习优化函数详解（2）– SGD 随机梯度下降 深度学习优化函数详解（3）– mini-batch SGD 小批量随机梯度下降 深度学习优化函数详解（4）– momentum 动量法 深度学习优化函数详解（5）– Neste
43-0309对数线性回归与广义线性回归-1080P 高清-AVC.mp4
最新发布
03-20
43-0309对数线性回归与广义线性回归-1080P 高清-AVC.mp4
41-0307多元线性回归-1080P 高清-AVC.mp4
03-20
41-0307多元线性回归-1080P 高清-AVC.mp4
37-0303一元线性回归-1080P 高清-AVC.mp4
03-20
37-0303一元线性回归-1080P 高清-AVC.mp4
线性回归-李沐老师-课堂笔记
04-13
线性回归-李沐老师-课堂笔记
10.MATLAB神经网络43个案例分析 RBF网络的回归-非线性函数回归的实现.rar
08-10
10.MATLAB神经网络43个案例分析 RBF网络的回归--非线性函数回归的实现10.MATLAB神经网络43个案例分析 RBF网络的回归--非线性函数回归的实现10.MATLAB神经网络43个案例分析 RBF网络的回归--非线性函数回归的实现10....
Linear-Regression-SGD：我将使用与以前相同的数据进行线性回归。 但是，我将使用优化器，特别是随机梯度下降
02-15
线性回归 我将使用与以前相同的数据进行线性回归。 但是，我将使用优化器，特别是随机梯度下降
深度学习之线性回归+基础优化
pengxiang1998的博客
07-12 1279
线性回归可以看作一个最简单的神经网络模型在我们开始考虑如何用模型拟合（）数据之前，我们需要确定一个拟合程度的度量。 损失函数（）能够量化目标的实际值与预测值之间的差距。 通常我们会选择非负数作为损失，且数值越小表示损失越小，完美预测时的损失为0。 回归问题中最常用的损失函数是平方误差函数。当样本的预测值为，其相应的真实标签为时， 平方误差可以定义为以下公式：.........
机器学习笔记(十四)——线性回归及其两种常用的优化方法
weixin_43434202的博客
05-01 3551
何为回归 回归的目的是预测数值型的目标值，最直接的办法是依据输入写出一个目标值的计算公式，比如要计算一个男生可以找到女朋友的概率： P=0.4∗财产+0.3∗长相+0.3∗身高P = 0.4\ast财产+0.3\ast长相+0.3\ast身高P=0.4∗财产+0.3∗长相+0.3∗身高 这意味着要综合财产、长相、身高三个因素来判断概率，其中财产也是最重要的因素。 这个式子就可以被称作回归方程，其中...
线性回归、线性回归的损失和优化
あずにゃん梓喵的博客
08-10 6191
日萌社 人工智能AI：Keras PyTorch MXNet TensorFlow PaddlePaddle 深度学习实战（不定时更新） 2.1 线性回归简介 1 线性回归应用场景 房价预测 销售额度预测 贷款额度预测 举例： 2 什么是线性回归 2.1 定义与公式 线性回归(Linear regression)是利用回归方程(函数)对一个或多个...
【AI数学】用梯度下降算法优化线性回归方程（含代码）
木盏
11-08 6488
众所周知，线性回归（Linear Regression）是最常见的机器学习算法之一，简单但超级实用。线性回归旨在用线性方程来拟合数据分布，在数据量小计算速度要求高的地方是神经网络的最佳替代品。
线性回归中的损失函数的数值表达式及向量表达式推导详解
weixin_71894495的博客
07-23 1929
本文通过一元线性回归为例推导出损失函数，并扩展成通用的多元线性回归方程的损失函数，以实际数据为例，转换为向量的表达形式
线性回归+基础优化算法笔记
m0_63276919的博客
10-13 1898
在每次迭代中，首先随机抽样一个小批量B， 它是由固定数量的训练样本组成的。最后，将梯度乘以一个预先确定的正数η，并从当前参数的值中减掉。此刻指的是根据生成的数据来拟合模型参数，开始小批量梯度下降更新参数，直到参数足够拟合数据。每次更新需要计算损失函数关于模型参数的梯度，利用梯度，通过减小损失的方向更新每个参数，利用自动微分来计算梯度。​ 从数据集中随机抽取小批量，根据参数计算损失的梯度，朝着减少损失的方向更新参数。解析解可以进行很好的数学分析，但解析解对问题的限制很严格，导致它无法广泛应用在深度学习里。
鲁棒线性回归问题，使用MindOpt也可优化
MindOpt_003的博客
03-17 1274
本篇我们讲述的是Linear Regression线性回归中的鲁棒线性回归。鲁棒回归又称为稳健回归，是统计学稳健估计的方法之一，主要思路是对离群点十分敏感的最小二乘回归中的的函数进行修改。
tensorflow 3. 线性回归和优化器
yuanlulu的博客
03-18 1527
本节例子在这里 本节例子主要计算Y=X*W + b公式里的W和b参数。优化器选用的是GradientDescentOptimizer。 我手工敲了一遍，翻译了注释，如下： import tensorflow as tf import numpy import matplotlib.pyplot as plt rng = numpy.random # 超参数 learning_rate ...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值